A calculator for the composition of functions is presented.
In the diagram below, function \( f \) has another function \( g \) as an input. Starting from the input \( x \), applying function \( g \) then function \( f \), we end up with a function called the composite function or composition of \( f \) and \( g \) denoted by \( f_o g \) and is defined by
\[ (f_o g)(x) = f(g(x)) \]
This composite function is defined if \(x \) is in the domain of \( g \) and \( g(x) \) is in the domain of \( f \). (see digram below).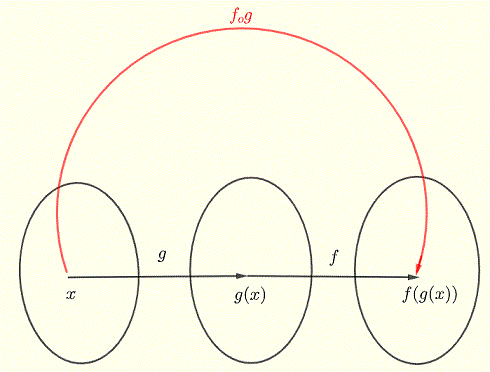
1 - Enter and edit functions \( f(x) \) and \( g(x) \) and click "Enter Functions" then check what you have entered and edit if needed.
2 - Press "Calculate Composition".
Note that the five operators used are: + (plus) , - (minus), / (division) , ^ (power) and * (multiplication). (example: f(x) = x^3+2*x^2 - 3*x -1 ).(more notes on editing functions are located below)
Notes: In editing functions, use the following:
1 - The function square root function is written as (sqrt). (example: sqrt(x^2-1)
2 - The exponential function is written as (e^x). (Example: e^(2*x+2) )
3 - The log base e function is written as ln(x). (Example: ln(2*x-2) )
Here are some examples of functions that you may copy and paste to practice:
sqrt(x) x^2 + 2x - 3 (x^2+2x-1)/(x-1) 1/(x-2) ln(2*x - 2)
sqrt(x^2-1)
2*sin(2x-2) e^(2x-3)
1/sqrt(x^2-1) x/(x+1)