Composition of Functions Examples
The definition and the properties of the composition of functions are discussed through examples with detailed solutions and explanations.
Definition of Composition of Functions
Let \( f \) and \( g \) be two functions. If we let function \( f \) take as input function \( g \) , see diagram below, the resulting function is called the composite function or composition of \( f \) and \( g \) denoted by \( f_o g \) and is defined by
\[ (f_o g)(x) = f(g(x)) \]
This composite function is defined if \(x \) is in the domain of \( g \) and \( g(x) \) is in the domain of \( f \). (see digram below).
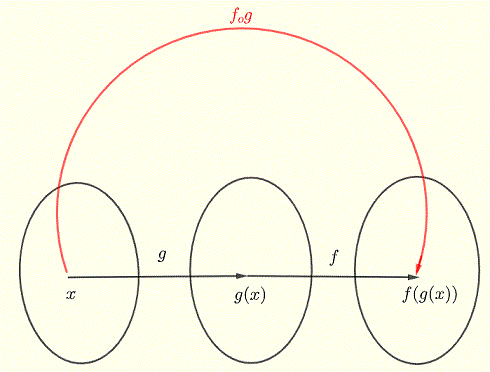
Examples with Solutions
Example 1: Composition of Functions Given Tables of Values
Functions \( f \) and \( g \) are defined by their tables as follows
| \( x \) | \( f(x) \) | | \( x \) | \( g(x) \) |
| 3 | 4 | | 2 | 6 |
| 5 | 7 | | 6 | 3 |
| 6 | 8 | | 7 | 9 |
| 8 | 11 | | 8 | 5 |
1) Find the values of:
a) \( (f_o g)( 2 )\) , b) \( (f_o g)( 6 )\) , c) \( (f_o g)( 7 )\) , d) \( (f_o g)( 8 )\)
e) \( (g_o f)( 3 ) \) , f) \( (g_o f)( 5 ) \) , g) \( (g_o f)( 6 ) \) , h) \( (g_o f)( 8 ) \)
i) \( (g_o g)( 2 ) \)
2) Find the domain of \( f_o g \) and \( g_o f \)
Solution to Example 1
1)
a)
Use definition of composition of functions to write
\( (f_o g)( 2 ) = f(g(2)) \)
Use table to find the value of \( g(2) = 6 \)
Substitute back in \( f(g(2)) \) to write
\( (f_o g)( 2 ) = f(g(2)) = f(6)\)
Use table to evaluate \(f(6)\)
\( (f_o g)( 2 ) = f(g(2)) = f(6) = 8\)
Use similar steps as above
b) \( (f_o g)( 6 ) = f(g(6)) = f(3) = 4 \)
c) \( (f_o g)( 7 ) = f(g(7)) = f(9) = \) undefined
d) \( (f_o g)( 8 ) = f(g(8)) = f(5) = 7\)
e) \( (g_o f)( 3 ) = g(f(3)) = g(4) = \) undefined
f) \( (g_o f)( 5 ) = g(f(5)) = g(7) = 9\)
g) \( (g_o f)( 6 ) = g(f(6)) = g(8) = 5\)
h) \( (g_o f)( 8 ) = g(f(8)) = g(11) = \) undefined
i) \( (g_o g)( 2 ) = g(g(2)) = g(6) = 3\)
2)
Use the results in part 1) to write the ordered pairs defining \( g_o f \) and \( f_o g \) and then deduce the domain.
\( g_o f : \{(2,6),(6,4),(8,7)\} \) , hence the domain of \( g_o f \) is given by: {2,6,8}
\( f_o g : \{(5,9),(6,5)\} \) , hence the domain of \( f_o g \) is given by: {5,6}
Example 2: Composition of Functions Given by their Graphs
Functions \( f \) and \( g \) are given by their graphs shown below
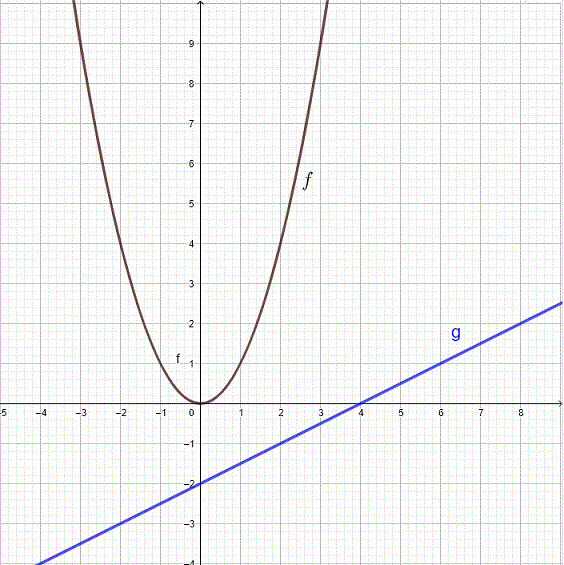
Find the values of:
a) \( (f_o g)( -2 )\) b) \( (f_o g)( 0 )\) c) \( (f_o g)( 4 )\) d) \( (f_o g)( 8 )\) e) \( (g_o f)( 2 )\) f) \( (g_o f)( 0 )\)
Solution to Example 2
a) Use definition of composition of functions to write
\( (f_o g)( -2 ) = f(g(-2)) \)
Use the graph of g to find the value of g(-2) = - 3
Substitute back in \( f(g(-2)) \) to write
\( (f_o g)( -2 ) = f(g(-2)) = f(-3) \)
Use the graph of f to evaluate \( f(-3) \)
\( (f_o g)( -2 ) = f(g(-2)) = f(-3) = 9 \)
Use similar steps as above to evaluate the following
b) \( (f_o g)( 0 ) = f(g(0)) = f(-2) = 4\)
c) \( (f_o g)( 4 ) = f(g(4)) = f(0) = 0\)
d) \( (f_o g)( 8 ) = f(g(8)) = f(2) = 4\)
e) \( (g_o f)( 2 ) = g(f(2)) = g(4) = 0\)
f) \( (g_o f)( 0 ) = g(f(0)) = g(0) = -2 \)
Example 3: Composition of Functions Given by their Formulas
Functions \( f \) and \( g \) are defined by the formulas: \( f(x) = 2x + 1 \) and \( g(x) = - x + 1 \)
a) Find the composite function \( (g_o f)( x ) \).
b) Find the composite function \( (f_o g)( x ) \).
Solution to Example 3
a)
Use the definition of composition of functions to write
\( (g_o f)( x ) = g(f(x)) \)
Express \( g(f(x)) \) in terms of \( f(x) \)
\( (g_o f)( x ) = g(f(x)) = - ( f(x) ) + 1 \)
Substitute \( f(x) \) by its formula
\( (g_o f)( x ) = g(f(x)) = - ( 2x + 1 ) + 1 \)
Simplify
\( (g_o f)( x ) = g(f(x)) = - ( 2x + 1 ) + 1 = - 2 x \)
b)
Use definition of composition of functions to write
\( (f_o g)( x ) = f(g(x)) \)
Express \( f(g(x)) \) in terms of \( g(x) \)
\( (f_o g)( x ) = f(g(x)) = 2 g(x) + 1\)
Substitute \( g(x) \) by its formula and simplify
\( (f_o g)( x ) = f(g(x)) = 2 g(x) + 1 = 2(- x + 1) + 1 = -2x + 3\)
Note that \( (g_o f)( x ) \ne (f_o g)( x ) \) , which means that the composition of functions is not commutative.
Example 4: Composition of Functions and their Domains
Functions \( f \) and \( g \) are defined by the formulas: \( f(x) = 2x + 1 \) and \( g(x) = \sqrt{x - 1} \)
Find the composite function \( (g_o f)( x ) \) and and its domain.
Solution to Example 4
\( (g_o f)( x ) = g(f(x)) = \sqrt{f(x) - 1} = \sqrt{2x+1 - 1} =\sqrt{2x}\)
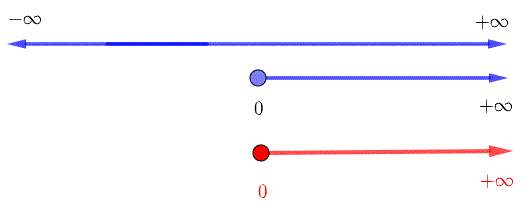
Two conditions for the domain of \( (g_o f) \)
1) \( x \) must be in the domain of \( f \) which is given by the interval : \( (-\infty , +\infty) \)
2) \( f(x) \) must be in the domain of \( g \) which is the domain of \( g(f(x)) \) .
The domain of \( g(f(x)) = \sqrt{2x} \) is found by solving the inequality: \( 2x \ge 0 \) wihich has the solution set given by the interval: \( [0 , + \infty) \)
The domain of \( (g_o f) \) is given by the intersection (red) of the sets in 1) and 2) ( in blue) : \( [0 , + \infty) \)
Example 5: Composition of Functions and their Domains
Functions \( f \) and \( g \) are defined by the formulas: \( f(x) = x^2 + 1\) and \( g(x) = \sqrt{4-x^2} \)
1) Find the composite function \( (f_o g)( x ) \) and and its domain.
2) Graph function \( f \), \( g \) and \( f_o g \) in the same system of coordinates.
Solution to Example 5
1)
\( (f_o g)( x ) = f(g(x)) = (g(x))^2 + 1 = (\sqrt{4-x^2})^2 + 1 = 5 - x^2 \)
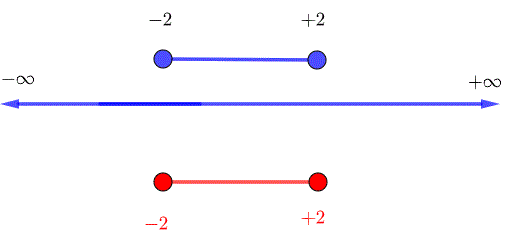
Two conditions for the domain of \( (f_o g) \)
1) \( x \) must be in the domain of g which is found by solving the inequality \( 4-x^2 \ge 0 \). The domain of g is given by the interval : \( [-2, + 2] \)
2) \( g(x) \) must be in the domain of f which is the domain of \( f(g(x)) \) which is the interval \( (-\infty , +\infty) \).
The domain of \( (f_o g) \) is given by the intersection (red) of the sets in 1) and 2) (blue) : \( [-2 , + 2] \)
2)
Below are shown the graphs of \( f \), \( g \) and \( f_o g \).

Properties of Composite Functions
Property 1
In general \( (f_o g)(x) \ne (g_o f)(x) \) and therefore the composition of functions is not commutative.
Example 3 above already shows that the composition of functions is not commutative.
Example 6: The composition is not commutative
Let \( f(x) = x^2 - 1 \) and \( g(x) = 2x \)
Show that \( (f_o g)(x) \ne (g_o f)(x) \)
Solution to Example 6
\( (f_o g)(x) = f(g(x)) = (g(x))^2 - 1 = (2x)^2 - 1 = 4x^2 - 1 \)
\( (g_o f)(x) = g(f(x)) = 2 f(x) = 2 (x^2 - 1) = 2x^2 - 2 \)
Therefore \( (f_o g)(x) \ne (g_o f)(x) \) and the composition of functions is not commutative.
Property 2
Let \( f, g \) and \( h \) be three functions, \( f_o (g_o h) = (f_o g)_o h \) and therefore the composition of funtions is associative.
Example 7: The composition of Functions is associative
Show that \( (f_o (g_o h))(x) = ((f_o g)_o h)(x) \)
Solution to Example 7
1) Left side
Use definition of composition to write
\( (f_o (g_o h))(x) = f((g_o h)(x)) \)
Use definition of composition again to write
\( = f(g(h(x)) \)
2) Right side
Use definition of composition to write
\( ((f_o g)_o h)(x) = (f_o g)(h(x)) \)
Use definition of composition to write
\( = f(g(h(x))) \)
Therefore
\( (f_o (g_o h))(x) = ((f_o g)_o h)(x) \)
Property 3
If \( f \) and \( g \) are invertible, then \( (f_o g)^{-1} = g^{-1}_o f^{-1} \)
Example 8: The inverse of the composition of Functions
Let \( f(x) = \dfrac{1}{x-1} \) and \( g(x) = - x + 5 \)
Show that \( (f_o g)^{-1} = g^{-1}_o f^{-1} \)
Solution to Example 8
We first calculate \( (f_o g)(x) \) and then its inverse \( (f_o g)^{-1}(x) \)
\( (f_o g)(x) = f(g(x)) = \dfrac{1}{g(x)-1} = \dfrac{1}{-x + 5 -1} = \dfrac{1}{-x + 4} \)
\( (f_o g)^{-1}(x) = - \dfrac{1}{x} + 4 \)
We now calculate the inverses \( f^{-1}(x) \) , \( g^{-1}(x) \) and then calculate the composition \( (g^{-1}_o f^{-1})(x) \).
\( f^{-1}(x) = \dfrac{1}{x} + 1 \)
\( g^{-1}(x) = - x + 5 \)
\( (g^{-1}_o f^{-1})(x) = g^{-1}(f^{-1}(x)) = - (f^{-1}(x)) + 5 = - ( \dfrac{1}{x} + 1) + 5 = - \dfrac{1}{x} + 4 \)
We conclude that
\( (g^{-1}_o f^{-1})(x) = (f_o g)^{-1}(x) \)
More References and links
Function composition
Composition of Functions Questions with Solutions
Applications of Composite Functions
Tutorial on Composition of Functions
Questions on Composite Functions with Solutions.




