Intercept Theorem and Problems with Solutions

The intercept theorem [1] also known as Thales's theorem is presented along with applications to problem solving.

Intercept Theorem

In all the figures below, \( BC \)is parallel to DE and both are intercepted by \( AD \) and \( AE \) with points of intersection at \( B, C, D \) and \( E \). intercept theorem part 1.
The intersect theorem states that the lengths of the segments are proportional as follows:
\[ \dfrac{\overline{AB}}{\overline{AD}} = \dfrac{\overline{AC}}{\overline{AE}} = \dfrac{\overline{BC}}{\overline{DE}} \quad \quad (I)\]
\[ \dfrac{\overline{AB}}{\overline{BD}} = \dfrac{\overline{AC}}{\overline{CE}} \quad \quad (II) \]
intercept theorem part 2. \[ \dfrac{\overline{FC}}{\overline{FB}} = \dfrac{\overline{GE}}{\overline{GD}} \quad \quad (III) \]

Problems with Solutions

Problem 1
In the figure below \( BC \) is parallel to \( DE \). Find \( \overline{AC} \) and \( \overline{BC} \)

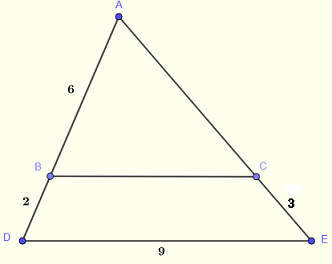
Solution to Problem 1
Acoording to the intercept theorem (I) above, we can write
            \( \dfrac{\overline{AB}}{\overline{AD}} = \dfrac{\overline{BC}}{\overline{DE}} = \dfrac{\overline{AC}}{\overline{AE}}\)

We can write two equations using the above proportions
            \( \dfrac{\overline{AB}}{\overline{AD}} = \dfrac{\overline{BC}}{\overline{DE}} \) (IV) and \( \dfrac{\overline{AB}}{\overline{AD}} = \dfrac{\overline{AC}}{\overline{AE}}\) (V)

Substitute the known lengths of segments in equation (IV)
            \( \dfrac{6}{6+2} = \dfrac{\overline{BC}}{9} \)

Use the cross product to rewrite the above equation as
            \( 8 \times \overline{BC} = 6 \times 9 \)

Solve for \( \overline{BC} \)
            \( \overline{BC} = 54/8 = 6.75 \)

Substitute the known lengths of segments in equation (V)
            \( \dfrac{6}{6+2} = \dfrac{\overline{AC}}{\overline{AC}+3}\)

Use the cross product to rewrite the above equation as
            \( 6 \times (\overline{AC}+3) = 8 \times \overline{AC} \)

Multiply and simplify
            \( 6 \overline{AC}+ 18 = 8 \overline{AC} \)

Group like terms
            \( 18 = 2 \overline{AC} \)

Solve for \( \overline{AC} \)
            \( \overline{AC} = 9 \)
Note that the triangles \( ABC \) and \( ADE \) are similar and therefore this problem can also be solved using similar triangle theorem.

Problem 2
In the figure below \( BC \) is parallel to \( DE \). Find \( \overline{DG} \), \( \overline{GE} \), \( \overline{AC} \) and \( \overline{CE} \).

intercept theorem two triangles problem 2

Solution to Problem 2

Using the intercept theorem (I) above, we can write
            \( \dfrac{\overline{AB}}{\overline{AD}} = \dfrac{\overline{BF}}{\overline{DG}} \)

Substitute the known lengths of segments in the above equation
            \( \dfrac{8}{8+2} = \dfrac{6}{\overline{DG}} \)

Use the cross product to rewrite the above as
           \( 8 \times \overline{DG} = 6 \times 10 \)

Solve for \( \overline{DG} \)
           \( \overline{DG} = 60 / 8 = 7.5 \)
Reuse the intercept theorem (I) above to write
            \( \dfrac{\overline{AB}}{\overline{AD}} = \dfrac{\overline{BC}}{\overline{DE}} \)

Substitute the known lengths of segments in the above equation.
            \( \dfrac{8}{8+2} = \dfrac{6+4}{\overline{DE}} \)

Use the cross product to rewrite the above equation as
           \( 8 \times \overline{DE} = 10 \times 10 \)

Solve for \( \overline{DE} \)
           \( \overline{DE} = 100 / 8 = 12.5 \)

Note that \( \overline{DE} = \overline{DG} + \overline{GE} \)
Hence
           \( \overline{GE}= \overline{DE} - \overline{DG} = 12.5 - 7.5 = 5 \)

Reuse the intercept theorem (I) above to write
            \( \dfrac{\overline{AC}}{\overline{FC}} = \dfrac{\overline{AE}}{\overline{GE}} \)

Note that \( \overline{AE} = \overline{AC} + \overline{CE} \)
Hence the above equation may be written as
            \( \dfrac{\overline{AC}}{4} = \dfrac{15}{5} \)

Use the cross product to rewrite the above equation as
           \( 5 \times \overline{AC} = 4 \times 15 \)

Solve the above to find
           \( \overline{AC} = 60/5 = 12 \)

and find \( \overline{CE} \) as follows
           \( \overline{CE} = \overline{AE} - \overline{AC} = 15 - 12 = 3\)

Problems 3
A technician wishes to determine the altitude of a ground-mounted long pole as follows (see figure below): He uses a light source at point \( B \) mounted on a structure of height 1 meters to shine a beam of light through the tops of both the short and long poles. The height of the short pole is 5 meters and the distance between the short pole and the long pole is 5 meters. The distance between the short pole and the structure supporting the light source is 2 meters. We assume that the structure supporting the light source and the two poles are all in the same plane and perpendicular to the ground. Find the altitude \( h \) of the long pole.

intercept theorem altitude of a pole problem 3

Solution to Problem 3
The light structure and the two poles are perpendicular to the ground and are therefore all parallel. Hence the use of the intercept theorem (I) to write
            \( \dfrac{\overline{OA}}{\overline{AB}} = \dfrac{\overline{OC}}{\overline{CD}} \)

Substitute the known lengths and \( \overline{OC} \) by \( \overline{OA} + 2 \)
            \( \dfrac{\overline{OA}}{1} = \dfrac{\overline{OA}+2}{5} \)

Cross multiply the above equation and rewrite as
            \( 5 \overline{OA} = \overline{OA}+2 \)

Solve for \( \overline{OA} \)
            \( \overline{OA} = 0.5 \) meters

Use the intercept theorem (I) one more time to write
            \( \dfrac{\overline{OA}}{\overline{AB}} = \dfrac{\overline{OF}}{h} \)

Substitute the known lengths
            \( \dfrac{0.5}{1} = \dfrac{0.5+2+5}{h} \)

Cross multiply the above equation and rewrite as
            \( 0.5 h = 7.5 \)

Solve for \( h \) to obtain
            \( h = 15 \) meters

Problems 4
In the figure below, the area of triangle \( OAB \) is 4 square units. \( AB \) is parallel to \( CD \). Find the area of triangle \( OCD \)

intercept theorem area of a triangle problem 4

Solution to Problem 4
Draw a segment through point \( O \) that is perpendicular to and intercept segments \( AB \) and \( CD \) at points \( L \) and \( M \) respectively as shown in the figure below.
intercept theorem area of a triangle problem 4 solution

intercept theorem area of a triangle problem 4 solution

Let \( A_1 \) and \( A_2 \) be the areas of triangles \( O A B \) and \( O D C \) respectively and use the formula for the area of a triangle (half the product of the altitude and base ) to write

\( A_1 = \dfrac{1}{2} \overline {OL} \times \overline {AB} \) and \( A_2 = \dfrac{1}{2} \overline {OM} \times \overline {CD} \)

Use of the intercept theorem (I) to write
            \( \dfrac{\overline{OM}}{\overline{OL}} = \dfrac{\overline{OD}}{\overline{OA}} = \dfrac{7.5}{2.5} = 3\)
and
            \( \dfrac{\overline{CD}}{\overline{AB}} = \dfrac{\overline{OD}}{\overline{OA}} = \dfrac{7.5}{2.5} = 3\)

From the above we can write that
            \( \dfrac{\overline{OM}}{\overline{OL}} \times \dfrac{\overline{CD}}{\overline{AB}} = 3 \times 3 = 9 \)

which may be written as
            \( \dfrac{\overline{OM} \times \overline{CD} }{\overline{OL} \times \overline{AB}} = 9 \)

Multiply the numerator and denominator in the above by \( 1/2 \) and write
            \( \dfrac{\frac{1}{2}\overline{OM} \times \overline{CD} }{ \frac{1}{2} \overline{OL} \times \overline{AB}} = 9 \)

The numerator and denominator in the above expression are the areas \( A_1 \) and \( A_2 \) as given by the formulas above, hence we may write that
            \( \dfrac{A_2}{ A_1} = 9 \)

Hence The ares \( A_2 \) of triangle \( O D C \) is given by:
            \( A_2 = 9 \times A_1 = 9 \times 4 = 36 \) square units.

Intercept Theorem and Problems with Solutions

Intercept Theorem

Problems with Solutions

More References and Links to Geometry Problems