Radius of a Circumscribed Circle Calculator
An online calculator to calculate the radius R of a circumscribed circle of a triangle of sides a, b and c.
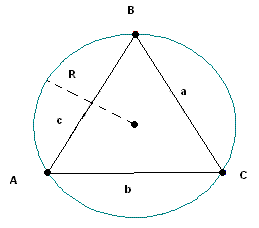
This calculator accepts the three sides of the triangle and uses the second of the formulas for the radius R of the circumscribed circle given below.
1) If you know one side of the triangle and the corresponding opposite angle, you may use the formula
\[ 2 R = \dfrac{a}{\sin(A)} = \dfrac{b}{\sin(B)} = \dfrac{c}{\sin(C)} \]
2) If you know all three sides, you may use the formula
\[ R = \dfrac{a \cdot b \cdot c}{4\sqrt{s(s-a)(s-b)(s-c)}} \]
where \( s = \dfrac{a+b+c}{2} \)
Use of Radius of Circumscribed Circle Calculator
Enter the sides a, b and c of the triangle as positive real numbers and press "Calculate". The output is the radius of the circumscribed circle. If one of the sides of the triangle is negative or the sum of any two positive sides is smaller that the third one (i.e the triangle does not exist), there will be no solution.
Example
Use the two formulas given above to find the radius of the circumscribed circle to the triangle with sides 6, 7 and 10 cm.
Solution
1) We use the first formula \( 2 R = \dfrac{a}{\sin(A)} \) by first using the cosine law to find angle A
\( a^2 = b^2 + c ^2 - 2 b c cos(A)) \)
\( cos(A) = \dfrac{a^2 - b^2 - c ^2}{-2 b c} \)
A = arccos \( \dfrac{a^2 - b^2 - c ^2}{-2 b c} \)
= arccos \( \dfrac{6^2 - 7^2 - 10 ^2}{-2 (7) (10) } = 36.18^{\circ} \)
R = \( 0.5 \dfrac{6}{\sin(36.18)} = 5.08\)
2) We now use the second formula
\( s = 0.5(a + b + c) = 0.5(6 + 7 + 10) = 11.5 \)
\( R = \dfrac{a \cdot b \cdot c}{ 4 \sqrt{s(s-a)(s-b)(s-c)}} = \dfrac{6 \cdot 7 \cdot 10}{4 \sqrt{11.5(11.5-6)(11.5-7)(11.5-10)}} = 5.08 \)
Use the calculator to check the results of the above example.
More References and Links
Radius of Circumcircle.
Online Geometry Calculators and Solvers.

