Graphing Linear Functions

Graph a linear function: a step by step tutorial with examples and detailed solutions. Free graph paper is available.


Linear Functions

Any function of the form f (x) = m x + b, where m is not equal to 0 is called a linear function. The domain of this function is the set of all real numbers. The range of f is the set of all real numbers. The graph of f is a line with slope m and y intercept b.
Note: A function f (x) = b, where b is a constant real number is called a constant function. Its graph is a horizontal line at y = b.

Example 1

Graph the linear function f given by
f (x) = 2 x + 4

Solution to Example 1

  • You need only two points to graph a linear function. These points may be chosen as the x and y intercepts of the graph for example.

  • Determine the x intercept, set f(x) = 0 and solve for x.

      2 x + 4 = 0

      x = - 2

  • Determine the y intercept, set x = 0 to find f(0).

      f(0) = 4

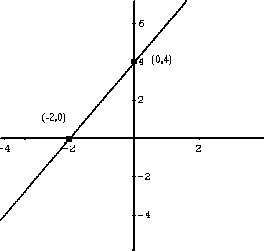
  • The graph of the above function is a line passing through the points (- 2 , 0) and (0 , 4) as shown below.
    graph of f(x)= 2 x + 4

Matched Problem
Graph the linear function f given by
f (x) = x + 3

Example 2

Graph the linear function f given by
f (x) = - (1 / 3) x - 1 / 2

Solution to Example 2

  • Determine the x intercept, set f(x) = 0 and solve for x.

      -(1 / 3) x - 1 / 2 = 0
      x = - 3 / 2

  • Determine the y intercept, set x = 0 to find f(0).
      f(0) = -1 / 2

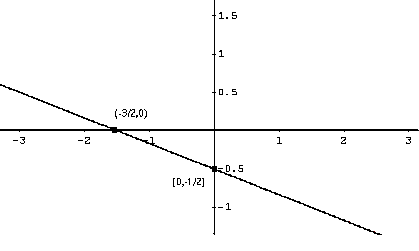
  • The graph of the above function is a line passing through the points (-3 / 2 , 0) and (0 , -1 / 2) as shown below.

    • graph of f(x)= -(3 / 2x - 1 / 2

Matched Problem 2
Graph the linear function f given by
f (x) = - x / 5 + 1 / 3

More References and Links to Graphing and Graphs of Functions

Graphing Functions
Solver to Analyze and Graph a Linear Function
Home Page