Example 1: Find the Points of Intersection of Two Hyperbolas
Find the points of intersection of the two hyperbolas given by their equations as follows:
\[ \dfrac{x^2}{4} - \dfrac{y^2}{16} = 1 \]
\[ \dfrac{(x - 1)^2}{2} - \dfrac{y^2}{4} = 1 \]
Solution to Example 1
- We first multiply all terms of the first equation by 16 and all the terms of the second equation by -4 to obtain equivalent equations: \[ 4x^2 - y^2 = 16 \] \[ -2(x - 1)^2 + y^2 = -4 \]
- We now add the corresponding sides of the two equations to obtain a single quadratic equation in terms of \(x\): \[ 4x^2 - 2(x - 1)^2 = 12 \]
- Expand and group like terms, then rewrite the equation in standard quadratic form: \[ 2x^2 + 4x - 14 = 0 \]
- Solve the quadratic equation for \(x\) using the quadratic formula to obtain two solutions: \[ x \approx 1.83 \quad \text{and} \quad x \approx -3.83 \]
- We now substitute the values of \(x\) obtained into the equation \(\dfrac{x^2}{4} - \dfrac{y^2}{16} = 1\) and solve for \(y\):
- For \(x \approx 1.83\), there are no real solutions for \(y\) because it yields a negative value under the radical for \(y^2\).
- For \(x \approx -3.83\): \[ \dfrac{(-3.83)^2}{4} - \dfrac{y^2}{16} = 1 \implies \dfrac{14.67}{4} - 1 = \dfrac{y^2}{16} \implies y \approx 6.53 \quad \text{and} \quad y \approx -6.53 \]
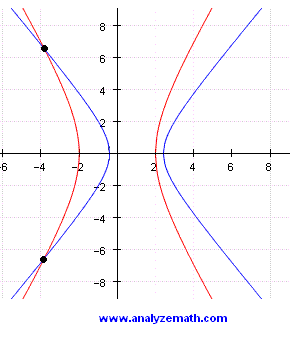
- Thus, the 2 points of intersection of the two hyperbolas are: \[ (-3.83, 6.53) \quad \text{and} \quad (-3.83, -6.53) \]
Shown below is the graph of the two hyperbolas and their points of intersection.
