أسئلة ومسائل حسابية القطع المكافئ مع حلول مفصلة

القطع المكافئ مسائل مع الإجابات و حلول مفصلة ، في الجزء السفلي من الصفحة.

\( \)\( \)\( \)\( \)

أسئلة

أوجد قطعتي x و y ، والرأس ومحور تناظر القطع المكافئ مع المعادلة \(y = - x ^ 2 + 2 x + 3 \)؟
ما هي نقاط تقاطع الخط المستقيم مع المعادلة \(2x + 3y = 7 \) والقطع المكافئ بالمعادلة \(y = - 2 x ^ 2 + 2 x + 5 \)؟
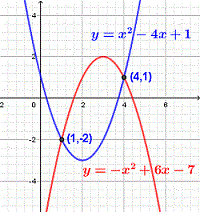
أوجد نقاط تقاطع القطعين المكافئين مع المعادلة \(y = - (x - 3) ^ 2 + 2 \) و \(y = x ^ 2 - 4x + 1 \).
أوجد معادلة القطع المكافئ \(y = 2 x ^ 2 + b x + c \) التي تمر عبر النقاط \((-1، -5) \) و \((2،10) \).
ما هي معادلة القطع المكافئ مع تقاطعات x عند \(x = 2 \) و \(x = -3 \) ، و a y - التقاطع عند \(y = 5 \)؟
أوجد معادلة القطع المكافئ \(y = a x ^ 2 + b x + c \) التي تمر عبر النقاط \((0،3) \)، \((1، -4) \) و \((-1 ، 4) \).
أوجد معادلة القطع المكافئ ، بمحور التناظر العمودي ، المماس للخط \(y = 3 \) عند \(x = -2 \) ويمر الرسم البياني الخاص به عبر النقطة \((0،5) \).
ما قيمة المنحدر m الخط ، مع المعادلة \(y = m x - 3 \) ، مماس للقطع المكافئ بالمعادلة \(y = 3 x ^ 2 - x \)؟
ما قيم المعلمة b التي يتقاطع فيها خط المعادلة \(y = 2 x + b \) مع القطع المكافئ للمعادلة \(y = - x ^ 2 - 2 x + 1 \) في نقطتين؟
أوجد المعادلة \(y = a x ^ 2 + x \) للقطع المكافئ المماس لخط المعادلة \(y = 3 x + 1 \).
انقل الرسم البياني للقطع المكافئ \(y = x ^ 2 \) إلى اليسار 3 وحدات ، ثم عكس الرسم البياني الناتج في المحور x ، ثم انقله لأعلى بمقدار 4 وحدات. ما هي معادلة القطع المكافئ الجديد بعد هذه التحولات؟
ما هي التحولات اللازمة لتحويل الرسم البياني للقطع المكافئ \(y = x ^ 2 \) إلى التمثيل البياني للقطع المكافئ \(y = - x ^ 2 + 4 x + 6 \)؟
اكتب معادلة القطع المكافئ الموضح في الرسم البياني أدناه.

حلول للأسئلة والمشاكل السابقة

تقاطعات x هي تقاطع القطع المكافئ مع المحور x ، وهي نقاط على المحور x ، وبالتالي فإن إحداثياتها y تساوي 0. لذلك ، يجب علينا حل المعادلة:
\( 0 = - x^2 + 2x + 3 \)
حلل الجانب الأيمن من المعادلة إلى عوامل أخرى:
\(- (x - 3) (x + 1) = 0 \)
تقاطعات x هي: حل من أجل x:
\(x = 3 \) y \(x = -1 \) ،
تقاطعات y هي تقاطع القطع المكافئ مع المحور y ، وهي نقطة على المحور y ، وبالتالي فإن إحداثياتها x تساوي 0
تقاطع y هو: \(y = - (0) ^ 2 + 2 (0) + 3 = 3 \) ،
يتم العثور على الرأس من خلال كتابة معادلة القطع المكافئ في شكل قمة \(y = a (x - h) ^ 2 + k \) بإكمال المربع وتحديد إحداثيات الرأس \(h \) و \(k \).
أكمل المربع:
\(y = - x ^ 2 + 2 x + 3 = - (x ^ 2-2 x - 3) = - ((x - 1) ^ 2-1 - 3) = - (x - 1 ) ^ 2 + 4 \)
الرأس عند النقطة \((1 ، 4) \)
يمكنك التحقق من جميع النقاط المذكورة أعلاه باستخدام الرسم البياني \(y = - x ^ 2 + 2 x + 3 \) الموضح أدناه.
نقاط التقاطع هي حلول المعادلات الآنية
\(2x + 3y = 7 \) و \(y = - 2 x ^ 2 + 2 x + 5 \).
بما أن \(y = - 2 x ^ 2 + 2 x + 5 \) ، استبدل \(- 2 x ^ 2 + 2 x + 5 \) عن y في المعادلة \(2x + 3y = 7 \) بالطريقة التالية
\( 2x + 3(- 2x^2 + 2x + 5) = 7 \)
اكتب المعادلة التربيعية التي تم الحصول عليها أعلاه في الشكل القياسي
\( -6x^2 + 8x + 8 = 0 \)
قسّم كل حدود المعادلة على 2.
\(-3x ^ 2 + 4x + 4 = 0 \)
حل ل x
\( x = 2 , x = -2/3 \)
عوّض بـ x بالحلول السابقة في \(2x + 3y = 7 \) لإيجاد y.
\( x = 2 , y = 1 \) and \( x = -2/3 , y = 25/9 \)
نقاط التقاطع هي: \((2 ، 1) \) و \((-2/3 ، 25/9) \).
تحقق من الإجابة بيانيا أدناه.
نقاط تقاطع القطعين المكافئين هي حلول المعادلات الآنية
\(y = - (x - 3) ^ 2 + 2 \) و \(y = x ^ 2 - 4x + 1 \).
احذف \(و \) واشتق المعادلة بمعرف واحد
\( -(x - 3)^2 + 2 = x^2 - 4x + 1 \)
\(-2x ^ 2 + 10x - 8 = 0 \)
\(-x ^ 2 + 5x - 4 = 0 \)
حلول المعادلة التربيعية أعلاه هي:
\(x = 1 \) and \(x = 4 \)
استخدم إحدى المعادلات لإيجاد y:
\(x = 1 \) في المعادلة \(y = - (x - 3) ^ 2 + 2 \) للحصول على \(y = - (1-3) ^ 2 + 2 = -2 \)
\(x = 4 \) في المعادلة \(y = - (x - 3) ^ 2 + 2 \) للحصول على \(y = - (4-3) ^ 2 + 2 = 1 \)
النقاط: \((1، -2) \) و \((4، 1) \)
تحقق من الإجابة بيانيا أدناه.
النقاط \((- 1 ، -5) \) و \((2،10) \) موجودة على الرسم البياني للقطع المكافئ \(y = 2 x ^ 2 + b x + c \) ، لذلك.
\( -5 = 2 (-1)^2 + b (-1) + c\)
\( 10 = 2 (2)^2 + b (2) + c\)
أعد كتابة النظام أعلاه في b و c بالشكل القياسي.
\( - b + c = - 7\)
\( 2b + c = 2\)
حل نظام المعادلات أعلاه للحصول على: \( c = - 4 \) and \( b = 3\)
معادلة القطع المكافئ الذي يمر عبر النقاط \((-1، -5) \) و \((2،10) \) هي:
\(y = 2 x ^ 2 + b x + c = 2 x ^ 2 + 3 × - 4 \)
استخدم مخطط الرسم البياني للتحقق من إجابتك عن طريق رسم بياني \(y = 2 x ^ 2 + 3 x - 4 \) & nbsp؛ و نبسب؛ تأكد من أن الرسم البياني يمر بالنقطتين \((- 1 ، -5) \) و \((2،10) \).
يمكن كتابة معادلة القطع المكافئ مع تقاطعات x عند \(x = 2 \) و \(x = -3 \) على أنها حاصل ضرب عاملين تكون أصفارهما هي تقاطع x على النحو التالي:
\( y = a(x - 2)(x + 3) \)
نستخدم الآن تقاطع y عند (0 ، 5) ، وهي نقطة يمر خلالها القطع المكافئ ، لكتابة:
\( 5 = a(0 - 2)(0 + 3) \)
حل من أجل \(a\)
\( a = - 5 / 6 \)
المعادلة: \( y = (-5/6)(x - 2)(x + 3)\)
رسم بياني \(y = (-5/6) (x - 2) (x + 3) \) وتحقق من أن الرسم البياني به تقاطع x عند \(x = 2، x = -3 \) و x- تقاطع عند y in \(y = 5 \).
النقاط \((0،3) ، (1 ، -4) \) و \((-1،4) \) تقع على الرسم البياني للقطع المكافئ \(y = a x ^ 2 + b x + c \) و لذلك هي حلول لمعادلة القطع المكافئ. لذلك نكتب نظام 3 معادلات على النحو التالي:
النقطة \((0،3) \) تعطي المعادلة: \(3 = a (0) ^ 2 + b (0) + c \quad (I) \)
النقطة \((1، -4) \) تعطي المعادلة: \( - 4 = a (1)^2 + b (1) + c \quad (II) \)
النقطة \((-1،4) \) تعطي المعادلة: \( - 4 = a (1)^2 + b (1) + c \quad (II) \)
المعادلة (I) تعطي:
\( c = 3 \)
البديل 3 لـ c في المعادلتين (II) و (III)
\( a + b = -7 \)
\( a - b = 1 \)
حل النظام في أ و ب
\( a = - 3 \) و \( b = - 4 \)
المعادلة: \(y = a x ^ 2 + b x + c = -3 x ^ 2 - 4x + 3 \)
ارسم بيانيًا بيانيًا لـ \(y = -3 x ^ 2 - 4x + 3 \) وتحقق من أن الرسم البياني يمر عبر النقاط \((0،3) ، (1 ، -4) \) و \((-1) ، 4) \).
معادلة القطع المكافئ ، بمحور التناظر العمودي ، لها الشكل \(y = a x ^ 2 + b x + c \) أو في شكل قمة \(y = a (x - h) ^ 2 + k \) حيث يكون الرأس عند النقطة \( (h , k)\) .
في هذه الحالة يكون مماسًا لخط أفقي \( y = 3 \) عند \( x = -2 \) مما يعني أن رأسه عند النقطة \( (h , k) = (-2 , 3) \). لذلك ، يمكن كتابة معادلة هذا القطع المكافئ على النحو التالي:
\(y = a (x - h) ^ 2 + k = a (x - (-2)) ^ 2 + 3 = a (x + 2) ^ 2 + 3 \)
يمر الرسم البياني الخاص به بالنقطة \((0 ، 5) \). لهذا
\( 5 = a(0 + 2)^2 + 3 = 4 a+ 3 \)
حل ما ورد أعلاه من أجل \ \( a \)
\( a = 1 / 2 \)
المعادلة: \( y = (1/2)(x + 2)^2 + 3 \)
ارسم الرسوم البيانية \(y = (1/2) (x + 2) ^ 2 + 3 \) وتحقق من أن الرسم البياني مماس للخط الأفقي \(y = 3 \) عند \( x = -2 \) لك الرسم البياني يمر بالنقطة \((0، 5) \).
يكون الخط والقطع المكافئ مماسًا إذا كان لهما نقطة تقاطع واحدة فقط ، وهي النقطة التي يتلامسان فيها.
تم العثور على نقاط التقاطع من خلال حل النظام
\( y = m x - 3 \) y \( y = 3 x^2 - x \)
\( mx - 3 = 3 x^2 - x \)
اكتب كمعادلة تربيعية قياسية:
\( 3 x^2 - x(1 + m) + 3 = 0 \)
يتم إعطاء مميز المعادلة التربيعية أعلاه من خلال:
\( \Delta = (1 + m)^2 - 4(3)(3) \)
يكون الخط مماسًا للقطع المكافئ للرسومات البيانية لمنحنيين لهما نقطة تقاطع إذا:
\(\ Delta = 0 \) (حالة حل المعادلة التربيعية)
ومن هنا جاءت المعادلة:
\( (1 + m)^2 - 4(3)(3) = 0 \)
حل لي
\( (1 + m)^2 = 36 \)
الحلول: \( m = 5 \) \( m = -7 \)
استخدم مخطط الرسم البياني للتحقق من إجابتك عن طريق رسم الرسوم البيانية للخطوط: \( y = 5 x - 3 \) (m = 5 حل) ، \(y = -7 x - 3 \) (m = 7 حل) والقطع المكافئ \(y = 3 x ^ 2 - x \) وتحقق من أن الخطين مماس للرسم البياني للقطع المكافئ \(y = 3 x ^ 2 - x \).
تم العثور على نقاط التقاطع من خلال حل النظام
\( y = 2 x + b \) و \( y = - x^2 - 2x + 1 \)
\( 2x + b = - x^2 - 2x + 1 \)
اكتب كمعادلة تربيعية قياسية:
\( - x^2 - 4x + 1 - b = 0 \)
يُعطى تمييز المعادلة أعلاه من خلال:
\(\Delta = (-4) ^ 2 - 4 (-1) (1 - b) = 20-4 \)
الرسوم البيانية \(y = 2 x + b \) و \(y = - x ^ 2 - 2 x + 1 \) تحتوي على نقطتي تقاطع إذا \( \Delta \gt 0 \) (حالة حلين حقيقيين من معادلة من الدرجة الثانية)
\( 20 - 4 b \gt 0 \)
حل من أجل b
\( b \lt 5 \)
استخدم مخطط الرسم البياني للتحقق من إجابتك عن طريق رسم الرسوم البيانية لـ \(y = - x ^ 2 - 2 x + 1 \) والخطوط من خلال المعادلات \(y = 2 x + b \) لقيم \( b \gt 5 \) و \(b \lt 5 \) و \(b = 5 \) لمعرفة عدد نقاط تقاطع القطع المكافئ والخط الموجود لكل من قيم \( b \) هذه.
تم العثور على نقاط التقاطع من خلال حل النظام
\( y = a x^2 + x \) y \( y = 3 x + 1 \)
\( 3 x + 1 = a x^2 + x \)
اكتب كمعادلة تربيعية قياسية:
\( a x^2 - 2 x - 1 = 0 \)
المميز:\( \Delta = (-2)^2 - 4(a)(-1) = 4 + 4 a \)
تكون الرسوم البيانية مماسة إذا كانت تحتوي على نقطة تقاطع (حالة لحل المعادلة التربيعية) إذا \(\ \Delta = 0 \). لهذا
\( 4 + 4 a = 0 \)
حل من أجل \(a\)
\( a = -1 \)
معادلة القطع المكافئ: \(y = -x ^ 2 + x \)
رسم بياني \(y = - x ^ 2 + x \) و \(y = 3 x + 1 \) للتحقق من الإجابة أعلاه.
البداية: \(y = x ^ 2 \)
انقل 3 وحدات إلى اليسار: \(y = (x + 3) ^ 2 \)
فكر في المحور السيني: \(y = - (x + 3) ^ 2 \)
انقل 4 وحدات لأعلى: \(y = - (x + 3) ^ 2 + 4 \)
معطى: \(y = - x ^ 2 + 4x + 6 \)
أعد الكتابة في شكل رأس بإكمال المربع: \(y = - x ^ 2 + 4 x + 6 = - (x - 2) ^ 2 + 10 \)
البداية: \(y = x ^ 2 \)
انقل وحدتين إلى اليمين: \(y = (x - 2) ^ 2 \)
فكر في المحور السيني: \( y = -(x - 2)^2 \)
انقل 10 وحدات لأعلى: \(y = - (x - 2) ^ 2 + 10 \)
يمكن استخدام أي نقطة محددة على الرسم البياني لإيجاد معادلة القطع المكافئ. ومع ذلك ، فإن استخدام تقاطع x و y والرأس هما أفضل الطرق لإيجاد معادلة القطع المكافئ الذي يظهر الرسم البياني أدناه.
يتم تقديم طريقتين لحل المشكلة:
الطريقة الأولى:
حتوي الرسم ا x لبياني على نقطتي تقاطع : (-5 ، 0) و (-1 ، 0)
استخدم تقاطعي x عند (-5 ، 0) و (-1 ، 0) لكتابة معادلة القطع المكافئ على النحو التالي:
\( y = a(x + 1)(x + 5)\)
استخدم تقاطع y عند (0 ، -5) للكتابة
\( - 5 = a(0 + 1)(0 + 5) = 5 a\)
حل من أجل \(a \)
\(a = -1\)
اكتب معادلة القطع المكافئ:
\( y = -(x + 1)(x + 5) = - x^2 -6 x - 5\)
الطريقة الثانية:
استخدم الرأس عند \((h، k) = (-3، 4) \) لكتابة معادلة القطع المكافئ في شكل قمة كما يلي:
\( y = a(x - h)^2 + k = a(x + 3)^2 + 4 \)
استخدم تقاطع y (0 ، -5) لإيجاد \ (a \).
\( - 5 = a(0 + 3)^2 + 4 \)
حل ما ورد أعلاه من أجل \(a\):
\( a = -1 \)
يتم إعطاء معادلة القطع المكافئ بواسطة
\(y = -(x + 3)^2 + 4 = - x^2 -6 x - 5 \)

أسئلة ومسائل حسابية القطع المكافئ مع حلول مفصلة

أسئلة

حلول للأسئلة والمشاكل السابقة

المزيد من المراجع والروابط على الأمثال