Difference Quotient
What is the difference quotient in calculus ?
We start with the definition and then we calculate the difference quotient for different functions as examples with detailed explanations.
Note that a difference quotient calculator is included and may be used to check results and generate further practice.
Definition of Difference Quotient
Let \( f \) be a function whose graph is shown below.
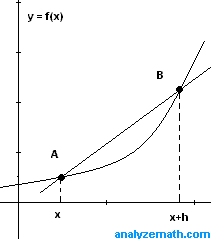
A and B are points on the graph of \( f\). A line passing trough the two points \( A ( x , f(x)) \) and \( B(x+h , f(x+h)) \) is called a secant line. The slope \( m \) of the secant line may be calculated as follows:
\[
m = \dfrac{f (x + h) - f(x)}{(x + h) - x}
\]
Simplify the denominator to obtain
\[
m = \dfrac{f (x + h) - f(x)}{h}
\]
The slope \( m \) is called the difference quotient. It is a very important concept in calculus where it is used to define the derivative of function \( f \) which in fact defines the local variation of a function in mathematics.
Examples with Solutions
In the examples below, we calculate and simplify the difference quotients of different functions.
Example 1
Find the difference quotient of function \( f \) defined by
\[f(x) = 2x + 5\]
Solution to Example 1
We first need to calculate \( f(x + h) \).
\[
f(x + h) = 2(x + h) + 5
\]
We now substitute \( f(x + h) \) and \( f(x) \) in the definition of the difference quotient by their expressions
\[
\dfrac{f (x + h) - f(x)}{h} = \dfrac{2(x + h) + 5 - (2 x + 5) }{h}
\]
We simplify the above expression.
\[
= \dfrac{2h}{2} = 2
\]
The answer is 2 which also the slope of the line defined by function \( f \), why?
Example 2
Find the difference quotient of the following function
\[ f(x) = 2x^2 + x - 2 \]
Solution to Example 2
We first calculate \( f(x + h) \).
\[
f(x + h) = 2(x + h)^2 + (x + h) - 2
\]
We now substitute \( f(x + h) \) and \( f(x) \) in the difference quotient
\[
\dfrac{f (x + h) - f(x)}{h}
= \dfrac{ 2(x + h)^2 + (x + h) - 2 - ( 2 x^2 + x - 2 )}{h}
\]
We expand the expressions in the numerator and group like terms.
\[
= \dfrac{ 4 x h + 2 h^2 + h}{h} = 4 x + 2 h +1
\]
Example 3
Find the difference quotient of function \( f \) given by
\[ f(x) = \sin x \]
and write the result as a product.
Solution to Example 3
We first calculate \( f(x + h) \).
\[
f(x + h) = \sin (x + h)
\]
We now substitute \( f(x + h) \) and \( f(x) \) in the difference quotient
\[
\dfrac{f (x + h) - f(x)}{h}
= \dfrac{ \sin (x + h) - \sin x}{h}
\]
We use the trigonometric formula that transform a difference \( \quad \sin (x + h) - \sin x \quad \) into a product.
\[
\sin (x + h) - \sin x = 2 \cos [ (2 x + h)/2 ] \sin (h/2)
\]
We substitute the above expression for \( sin (x + h) - sin x \) in the difference quotient above to obtain.
\[
\dfrac{f (x + h) - f(x)}{h}
= \dfrac{ 2 \cos [ (2 x + h)/2 ] \sin (h/2)}{h}
\]
More References and links
Difference Quotient Calculator
differentiation and derivatives
Difference quotient

