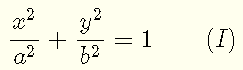
The conversion from rectangualar to polar coordinates is given by
Substitute the above in equation (I)
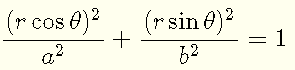
Divide all terms in the above equation by
and simplify
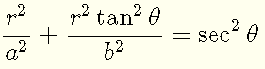Solve for r2
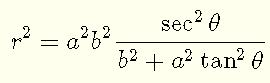
The equation of an ellipse centered at the origin is given by
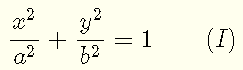
The conversion from rectangualar to polar coordinates is given by
Substitute the above in equation (I)
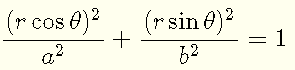
Divide all terms in the above equation by
and simplify
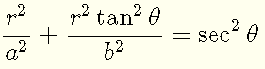Solve for r2
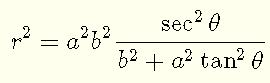
The area \( A \) in polar coordinate enclosed by a curve is given by the formula
\[ A = \dfrac{1}{2} \int_0^{2\pi} r(\theta)^2 d \theta \]
where \( r(\theta) \) is the equation of the curve in polar coordinates,
Substitute \( r^2 \) of the ellipse found above
\[ A = \dfrac{1}{2} \int_0^{2\pi} a^2 b^2 \dfrac{\sec^2 \theta}{b^2+a^2\tan^2 \theta} d\theta \qquad (II) \]
Use the trigonometric substitution method that transform \( \quad a \tan \theta \) into \( b \tan \alpha \quad \) so that the denominator can be factored and hence more simplifications occur.
Let \[ b \tan \alpha = a \tan \theta \qquad (III) \]
Differentiate both sides of the above with respect to \( \theta \), using the chain rule of differentiation on the left side,
\[ b \sec^2 \alpha \dfrac{d \alpha}{d \theta } = a \sec^2 \theta \]
which gives
\[ \sec^2 \theta d \theta = \dfrac{b}{a} \sec^2 \alpha \; d \alpha \]
or
\[ d \theta = \dfrac{\dfrac{b}{a} \sec^2 \alpha}{\sec^2 \theta } \; d \alpha \qquad (IV)\]
Limits of integration
From (III) above, we may write \( \alpha = \arctan (\dfrac{a}{b} \tan \theta ) \)
For \( \theta = 0 \) , \( \alpha =0 \)
For \( \theta = 2\pi \) , \( \alpha = 2\pi \)
Substitute \( d\theta \) in (IV) and the limits of integration in the integral
\[ A = \dfrac{1}{2} \int_0^{2\pi} a^2 b^2 \dfrac{\sec^2 \theta}{b^2+b^2\tan^2 \alpha} \dfrac{\dfrac{b}{a} \sec^2 \alpha}{\sec^2 \theta } \; d \alpha \]
Factor \( b^2 \) in the denominator and take all constant outside the integral and simplify
\[ A = \dfrac{ a b}{2} \int_0^{2\pi} \dfrac{1}{1+\tan^2 \alpha} \sec^2 \alpha \; d \alpha \]
Use the trigonometric identity \( 1+1\tan^2 \alpha = \sec^2 \alpha \) in the denominator and simplify
\[ A = \dfrac{ a b}{2} \int_0^{2\pi} d \alpha \]
Evaluate the integral
\[ A = \dfrac{ a b}{2} \left[\alpha\right]_0^{2\pi} d \alpha \]
Simplify
\[ A = a b \pi \]
