The first derivative is used to minimize (optimize) distance travelled between two points.
Problem
The diagram below shows the path that Wilson follows every morning to take water from the river to his farm. Help Wilson minimize the total distance travelled from his house to the farm.
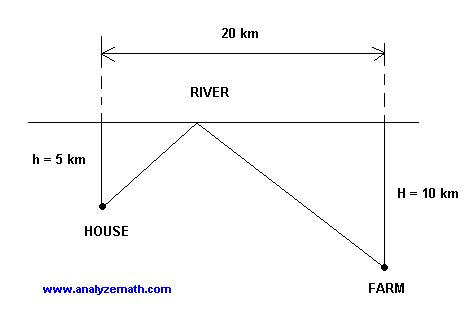
Solution to the Problem
Two methods, to solve this problem, are suggested.
METHOD 1: In the diagram below we find the distances \(d\) and \(D\) add them and minimize the total distance.
\[d = \sqrt{x^2 + 5^2}\]
\[D = \sqrt{(20 - x)^2 + 10^2}\]
The total distance \(T\) is given by.
\[T = d + D = \sqrt{x^2 + 5^2} + \sqrt{(20-x)^2 + 10^2}\]
We now need to find the first derivative \(\dfrac{dT}{dx}\) of \(T\) with respect to \(x\) and check that \(T\) has a minimum value then find the value of \(x\) that minimizes \(T\).
\[\dfrac{dT}{dx} = \dfrac{x \sqrt{(x - 20)^2 + 100} + (x - 20) \sqrt{x^2 + 25}}{\sqrt{x^2 + 25} + \sqrt{(x - 20)^2 + 100}}\]
The graph of \(\dfrac{dT}{dx}\) is shown below. At approximately \(x = 6.6\), the first derivative is equal to zero; below that value it is negative and above that same value it is positive. Hence \(T\) has a minimum value at around \(x = 6.6\). Let us find the exact value by calculation
The value of \(x\) that makes \(T\) minimum is found by setting \(\dfrac{dT}{dx} = 0\) and solving the equation obtained. It is called a critical value of the first derivative. \(\dfrac{dT}{dx} = 0\) gives
\[x \sqrt{(x - 20)^2 + 100} + (x - 20) \sqrt{x^2 + 25} = 0\]
which may be written as
\[x \sqrt{(x - 20)^2 + 100} = - (x - 20) \sqrt{x^2 + 25}\]
Square both sides
\[x^2((x - 20)^2 + 100) = (x - 20)^2(x^2 + 25)\]
Expand and simplify to obtain the quadratic equation
\[3x^2 + 40x - 400 = 0\]
Solve for \(x\) and select the positive value
\[x = \dfrac{20}{3} = 6.67 \text{ km}\] (approximately)
METHOD 2: We "construct a virtual house" (projection) \(H\) on the other side of the river and then for the distance \(d + D\) to be minimum we need to have the points \(H\), \(O\) and \(F\) to be collinear since the shortest distance between two points is along a straight line. For these points to be on the same line angle \(HOH'\) have to be equal (in size) to angle \(FOF'\) and the tangent of the two angles have to be equal. Hence
Calculate the tangent in terms of \(x\) for both angles as follows
\[\tan(HOH') = \dfrac{5}{x}\]
\[\tan(FOF') = \dfrac{10}{20 - x}\]
\[\dfrac{10}{20 - x} = \dfrac{5}{x}\]
Solve for \(x\) to obtain
\[x = \dfrac{20}{3} = 6.67 \text{ km}\] (approximately)
