Sinuskurven und Kosinuskurven zeichnen

Graphen der Sinus- und der Kosinusfunktionen der Form \[ \Large \mathbf { \color{red}{ y = a \sin(b x + c) + d}} \] und \[ \Large \mathbf { \color{red}{ y = a \cos(b x + c) + d}} \] werden anhand mehrerer Beispiele mit detaillierten Lösungen besprochen.

Wir beginnen mit dem Graphen der grundlegenden Sinusfunktion $ y = \sin(x) $ und der grundlegenden Kosinusfunktion $ g(x) = \cos(x) $ und zeigen dann Beispiele, wie transformierte Versionen dieser Funktionen gezeichnet werden. Eine effektive Methode, dieses Tutorial zu nutzen, besteht darin, es von Anfang an zu starten und die Beispiele der Reihe nach durchzugehen.

Graph der grundlegenden Sinusfunktion: $ y = \sin(x) $

Beispiel 1

Finden Sie den Wertebereich und die Periode der Funktion $ y = \sin(x) $ und zeichnen Sie sie.

Lösung zu Beispiel 1

Ein Einheitskreis (mit Radius 1) mit dem Mittelpunkt im Ursprung des rechtwinkligen Achsensystems hat 4 spezielle Punkte, die 5 Quadrantenwinkeln entsprechen $ (0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi ) $, wie in Abbildung 1 unten gezeigt. Die $ x $- und $ y $-Koordinaten eines Punktes auf dem Einheitskreis sind der Kosinus bzw. der Sinus des entsprechenden Winkels.

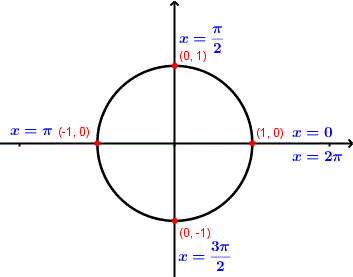
Abbildung 1. Einheitskreis in der Trigonometrie

$ x $ sei der Winkel in Normalposition . Aus dem Einheitskreis können wir Folgendes ableiten:

Der Wertebereich von $ \sin(x) $ (die y-Koordinaten) ist die Menge aller Werte im Intervall \[ [-1 , 1] \; \text{oder in Ungleichungsform} \; -1 \leq \sin(x) \leq 1 \]

Ein Zyklus von $ \sin(x) $ kann bei $ x = 0 $ beginnen und bei $ x = 2\pi $ enden, wonach sich die Werte von $ \sin(x) $ wie im Einheitskreis gezeigt wiederholen. Wir sagen daher, dass $ \sin(x) $ eine Periode von $ 2\pi $ hat.

Wir benötigen Werte von $ \sin(x) $ für verschiedene Werte von $ x $, um sie zu zeichnen. Wir verwenden die y-Koordinate (die $ \sin(x) $ ergibt) derselben 5 Quadrantenwinkel, die der Variablen $ x (0 ,\dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi) $ entsprechen. Von diesen sind 3 Werte $ (0 , \pi , 2 \pi) $ Nullstellen von $ \sin(x) $, ein Wert $ (\dfrac{\pi}{2}) $ ergibt einen Maximalwert für $ \sin(x) $ und ein Wert $ ( \dfrac{3\pi}{2} ) $ ergibt einen Minimalwert für $ \sin(x) $, wie in der Tabelle unten gezeigt. \[ \begin{array}{|c|c|c|} \hline x & y = \sin(x) \\ \hline 0 & 0 \\ \dfrac{\pi}{2} & 1\\ \pi & 0 \\ 3\dfrac{\pi}{2} & -1 \\ 2 \pi & 0 \\ \hline \end{array} \] Der Graph von $ y = \sin(x) $ ist unten über eine Periode von $ 0 $ bis $ 2\pi $ (durchgezogene Linie) und weitere Perioden (gestrichelte Linie) dargestellt.

Graph von y = sin(x) — Abbildung 2. Graph von $ y = \sin(x) $

Graph der grundlegenden Kosinusfunktion: $ f(x) = \cos(x) $

Beispiel 2

Finden Sie den Wertebereich und die Periode der Funktion $ y = \cos(x) $ und zeichnen Sie sie.

Lösung zu Beispiel 2

Wir werden dieselben 4 speziellen Punkte verwenden, die den 5 Quadrantenwinkeln $ 0 , \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2} \text{ und } 2\pi $ entsprechen, wie im Einheitskreis (Abbildung 1 oben) gezeigt. $ \cos(x) $ wird durch die x-Koordinate eines Punktes auf dem Einheitskreis angegeben, der dem Winkel $ x $ in Normalposition entspricht.

Aus dem Einheitskreis können wir Folgendes ableiten:

Der Wertebereich von $ \cos(x) $ ist die Menge aller Werte im Intervall $[-1 , 1]$ in Ungleichungsform: \[ -1 \leq \cos(x) \leq 1 \]

Ein Zyklus von $ \cos(x) $ kann bei $ x = 0 $ beginnen und bei $ x = 2\pi $ enden, wonach sich der Wert von $ \cos(x) $ wie im Einheitskreis gezeigt periodisch wiederholt. Wir schließen daraus, dass $ \cos(x) $ eine Periode von $ 2\pi $ hat.

Wir verwenden die Werte von $ \cos(x) $ für verschiedene Werte von $ x $ aus dem Einheitskreis (siehe Abbildung 1). Wir werden die x-Koordinate (die $ \cos(x) $ ergibt) derselben 5 Quadrantenwinkel verwenden, die der Variablen $ x $ entsprechen: $ 0 , \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, \text{ und } 2\pi $. Von diesen ergeben zwei Werte ($ 0 , 2\pi $) den Maximalwert $ 1 $ von $ \cos(x) $, zwei Werte $ \dfrac{\pi}{2} $ und $ \dfrac{3\pi}{2} $ ergeben Nullstellen von $ \cos(x) $, und ein Wert $ \pi $ ergibt einen Minimalwert für $ \cos(x) $, wie in der Tabelle unten gezeigt. \[ \begin{array}{|c|c|c|} \hline x & y = \cos(x) \\ \hline 0 & 1 \\ \dfrac{\pi}{2} & 0 \\ \pi & -1 \\ 3\dfrac{\pi}{2} & 0 \\ 2 \pi & 1 \\ \hline \end{array} \] Der Graph von $ \cos(x) $ ist unten über eine Periode von $ 0 $ bis $ 2\pi $ (durchgezogene Linie) und weiteren Perioden (gestrichelte Linie) dargestellt.

Graph von y = cos(x) — Abbildung 3. Graph von $ y =\cos(x) $

Graph der Funktion: $ y = 3\sin(x) $

Beispiel 3

Finden Sie den Wertebereich und die Periode der Funktion $ y = 3\sin(x) $ und zeichnen Sie sie.

Lösung zu Beispiel 3

Beim Vergleich der gegebenen Funktion $ y = 3 \sin(x) $ mit der grundlegenden Sinusfunktion $ y = \sin(x) $ gibt es einen Multiplikationsfaktor von 3. Es gibt keine horizontale Streckung oder Verschiebung, da die Variable $ x $ in beiden Funktionen auf dieselbe "Weise" vorkommt. \[ \text{Periode} = 2\pi \] Wir haben bereits oben eine Tabelle für $ \sin(x) $ erstellt; erweitern wir sie um die gegebene Funktion $ y = 3 \sin(x) $ zum Zeichnen. Hinweis: Um Werte für die Funktion $ 3 \sin(x) $ zu erhalten, multiplizieren Sie die Werte der Funktion $ \sin(x) $ mit 3, wie in der Tabelle unten gezeigt. Aus der Tabelle: \[ \text{Wertebereich: } -3 \leq 3 \sin(x) \leq 3 \] \[ \begin{array}{|c|c|c|} \hline x & \sin(x) & y = 3 \sin(x) \\ \hline 0 & 0 & 0 \\ \dfrac{\pi}{2} & 1 & 3 \\ \pi & 0 & 0 \\ 3\dfrac{\pi}{2} & -1 & -3 \\ 2 \pi & 0 & 0 \\ \hline \end{array} \] Der Graph von $ 3 \sin(x) $ ist unten über eine Periode von 0 bis 2π dargestellt, und wie erwartet gibt es eine vertikale Streckung um den Faktor 3 (im Vergleich zu $ y = \sin(x) $, rot). Die Periode hat sich wie erwartet nicht geändert, aber der Wertebereich ist jetzt: $ [-3 , 3] $ oder in Ungleichungsform: $ -3 \leq 3 \sin(x) \leq 3 $

Graph von y = 3sin(x) — Abbildung 4. Graph von $ y = 3 \sin(x) $

Graph der Funktion: $ y = - 2 \cos(x) $

Beispiel 4

Finden Sie den Wertebereich und die Periode der Funktion $ y = -2 \cos(x) $ und zeichnen Sie sie.

Lösung zu Beispiel 4

Beim Vergleich der gegebenen Funktion $ y = - 2 \cos(x) $ mit der grundlegenden Kosinusfunktion $ y = \cos(x) $ gibt es eine vertikale Streckung um den Faktor 2 und es gibt auch eine Spiegelung an der x-Achse aufgrund des Minuszeichens in -2. Es gibt keine horizontale Streckung oder Verschiebung, da die Variable x in beiden Funktionen auf dieselbe "Weise" vorkommt.

Periode = 2π

Eine Tabelle für $ \cos(x) $ wurde bereits oben erstellt, erweitern wir sie um die gegebene Funktion $ y = - 2 \cos(x) $ zum Zeichnen.

Aus der Tabelle; Wertebereich: $ -2 \leq -2 \cos(x) \leq 2 $

Im Allgemeinen ist der Wertebereich von Funktionen der Form $ y = a \sin(x) $ oder $ y = a \cos(x) $ durch das Intervall \[ [ - |a| , |a| ] \; \text{oder in Ungleichungsform} - |a| \le y \le |a| \] \[ \begin{array}{|c|c|c|} \hline x & \cos(x) & y = -2 \cos(x) \\ \hline 0 & 1&-2 \\ \dfrac{\pi}{2} & 0 & 0 \\ \pi & -1& 2 \\ 3\dfrac{\pi}{2} & 0 & 0 \\ 2 \pi & 1 &-2 \\ \hline \end{array} \]

Der Graph von $ -2 \cos(x) $ ist unten über eine Periode von $ 0 $ bis $ 2\pi $ (durchgezogene blaue Linie) im Vergleich zu $ y = \cos(x) $ (rot) dargestellt, und wir können erkennen, dass es eine Streckung um den Faktor 2 und eine Spiegelung gibt.

Graph von y = - 2 cos(x) — Abbildung 5. Graph von $ y = -2 \cos(x) $

Graph der Funktion: $ y = \sin(2 x) $

Beispiel 5

Finden Sie die Periode der Funktion $ y =\sin(2 x) $ und zeichnen Sie sie.

Lösung zu Beispiel 5

Beim Vergleich der gegebenen Funktion $ y = \sin(2 x) $ mit der grundlegenden Sinusfunktion $ y = \sin(x) $ gibt es eine horizontale Stauchung um den Faktor $ 2 $ wegen des $ 2x $ in $ \sin(2 x) $.

Erklärung Für die Funktion $ y =\sin(2 x) $, um einen Zyklus zu durchlaufen, muss $ 2 x $ wie folgt sein \[0 \leq 2x \leq 2\pi \] Teilen Sie alle Terme der obigen Ungleichung durch $ 2 $, wir erhalten \[ 0 \leq x \leq \pi \] Dies ist das Intervall über eine Periode, das verwendet wird, um $ y =\sin(2 x) $ zu zeichnen. Daher ist die Periode von $ \sin(2x) $ gegeben durch \[ \pi - 0 = \pi \]

Im Allgemeinen ist die Periode von Funktionen der Form $ y = \sin( b x) $ oder $ y = \cos( b x) $ gegeben durch \[ \dfrac{\ 2\pi}{|b|} \] Die Periode ist immer positiv. Eine Tabelle für $ \sin(2 x) $ wird auf ähnliche Weise erstellt wie für $ y = \sin(x) $, mit einem Unterschied in den Werten von $ x $ über eine Periode von $ 0 $ bis $ \pi $ (eine Periode).

Die Werte $ x = 0, \pi , \pi/4 , \pi/2 , 3\pi/4 $ unterteilen die Periode in 4 gleiche Intervalle. \[ \begin{array}{|c|c|c|} \hline x & y = \sin(2 x) \\ \hline 0 & 0\\ \dfrac{\pi}{4} & 1 \\ \dfrac{\pi}{2} & 0 \\ 3\dfrac{\pi}{4} & -1\\ \pi & 0\\ \hline \end{array} \] Der Graph von $ y = \sin(2 x) $ ist unten über eine Periode von $ 0 $ bis $ \pi $ (durchgezogene blaue Linie) im Vergleich zu $ y =\sin(x) $, das eine Periode von $ 2\pi $ hat (rot), dargestellt.

Graph von y =\sin(2x) — Abbildung 6. Graph von $ y = \sin(2x) $

Graph der Funktion: $ y = \cos(2 x - \dfrac{\pi}{4}) $

Beispiel 6

Finden Sie die Periode und die Phasenverschiebung der Funktion $ y = \cos\left(2x - \dfrac{\pi}{4}\right) $ und zeichnen Sie sie.

Lösung zu Beispiel 6

Schreiben Sie die gegebene Funktion um als \[ y = \cos\left(2(x - \dfrac{\pi}{8})\right) \] Wir beginnen zunächst damit, den Term $ -\dfrac{\pi}{8} $ zu ignorieren und eine Periode für $ y = \cos(2x) $ zu definieren \[ 0 \leq 2x \leq 2\pi \] Teilen Sie alle Terme durch 2, um zu erhalten \[ 0 \leq x \leq \pi \] Die Periode ist $ \pi $, wie bereits oben berechnet.

Für die Funktion $ y = \cos\left(2(x - \dfrac{\pi}{8})\right) $, um einen Zyklus zu durchlaufen, muss der Ausdruck $ 2(x - \dfrac{\pi}{8}) $ wie folgt sein: \[ 0 \leq 2(x - \dfrac{\pi}{8}) \leq 2\pi \] Teilen Sie alle Terme durch 2 \[ 0 \leq x - \dfrac{\pi}{8} \leq \pi \] Addieren Sie $ \dfrac{\pi}{8} $ zu allen Termen \[ \dfrac{\pi}{8} \leq x \leq \pi + \dfrac{\pi}{8} \] Dies ist das Intervall über eine Periode, das verwendet wird, um $ y = \cos\left(2x - \dfrac{\pi}{4}\right) $ zu zeichnen.

Wenn wir das Intervall einer Periode für $ \cos(2x) $, das ist \[ 0 \leq x \leq \pi \] und das Intervall für eine Periode von $ \cos\left(2(x - \dfrac{\pi}{8})\right) $, das ist \[ \dfrac{\pi}{8} \leq x \leq \pi + \dfrac{\pi}{8} \] vergleichen, ist der einzige Unterschied die Phasenverschiebung nach rechts um $ \dfrac{\pi}{8} $

Im Allgemeinen ist die Phasenverschiebung von Funktionen der Form $ y = \sin(bx + c) $ oder $ y = \cos(bx + c) $ gegeben durch \[ -\dfrac{c}{b} \] Wenn die Phasenverschiebung positiv ist, ist die Verschiebung nach rechts, und wenn sie negativ ist, ist die Verschiebung nach links.

Wir erstellen die Wertetabelle wie folgt:

Wir haben oben gesehen, dass in diesem Beispiel eine Periode bei $ x = \dfrac{\pi}{8} $ beginnt und bei $ x = \pi + \dfrac{\pi}{8} = \dfrac{9\pi}{8} $ endet. Daher beginnen wir die Tabelle mit diesen beiden Punkten.

Eine Periode

Wir finden als nächstes den Mittelwert zwischen $ x = \pi/8 $ und $ x = 9\pi/8 $, berechnet wie folgt: \[ \dfrac{1}{2} \left( \dfrac{\pi}{8} + \dfrac{9\pi}{8} \right) = \dfrac{5\pi}{8} \] und fügen ihn in die Tabelle ein.

Drei Punkte in einer Periode

Wir finden als nächstes den Mittelwert zwischen $ x = \pi/8 $ und $ 5\pi/8 $, berechnet wie folgt: $ \frac{1}{2}(\pi/8 + 5\pi/8) = 3\pi/8 $; und den Mittelwert zwischen $ 5\pi/8 $ und $ 9\pi/8 $, berechnet wie folgt: $ \frac{1}{2}(5\pi/8 + 9\pi/8) = 7\pi/8 $, und fügen alle diese in die Tabelle ein.

Wir finden den Mittelwert zwischen $ x = \dfrac{\pi}{8} $ und $ \dfrac{5\pi}{8} $, berechnet wie folgt: \[ \dfrac{1}{2} \left( \dfrac{\pi}{8} + \dfrac{5\pi}{8} \right) = \dfrac{3\pi}{8} \] und den Mittelwert zwischen $ \dfrac{5\pi}{8} $ und $ \dfrac{9\pi}{8} $, berechnet wie folgt: \[ \dfrac{1}{2} \left( \dfrac{5\pi}{8} + \dfrac{9\pi}{8} \right) = \dfrac{7\pi}{8} \] und fügen alle diese in die Tabelle ein.

Fünf Punkte in einer Periode

Wir haben das Ein-Perioden-Intervall in 4 gleiche Intervalle unterteilt, und diese erleichtern die Auswertung der gegebenen Funktion $ y =\sin(2x) $, die dieselben Maximal- und Minimalwerte an ähnlicher Stelle, aber innerhalb des Intervalls $ \dfrac{\pi}{8} , \dfrac{9\pi}{8} $ haben wird. Wir vervollständigen nun die Tabelle, indem wir die Werte der Funktion eintragen.

Werte von y = cos(2 x - pi/4)

Der Graph von $ y = \cos(2 x - \dfrac{\pi}{4}) $ (blau) wird mit dem Graphen von $\cos(2 x) $ (rot) verglichen. Sie sind ähnlich, bis auf die Verschiebung um $ \dfrac{\pi}{8} $ nach rechts.

Graph von y = cos(2x - pi/4) — Abbildung 7. Graph von $ y = \cos(2 x - \dfrac{\pi}{4}) $

Graph der Funktion: $ y =\sin(3 x + \dfrac{\pi}{3}) $

Beispiel 7

Finden Sie die Periode und die Phasenverschiebung der Funktion $ y =\sin(3 x + \dfrac{\pi}{3}) $ und zeichnen Sie sie.

Lösung zu Beispiel 7

Die Periode ist gegeben durch: \[ \dfrac{2\pi}{|b|} = \dfrac{2\pi}{3} \]

Die Phasenverschiebung wird wie folgt berechnet: \[ \dfrac{-c}{b} = \dfrac{-\pi/3}{3} = \dfrac{-\pi}{9} \]

Wir erwarten, dass der Graph von $ y = \sin(3x + \dfrac{\pi}{3}) $ der Graph von $ y = \sin(3x) $ ist, verschoben um $ \dfrac{\pi}{9} $ nach links wegen des Minuszeichens in der Phasenverschiebung.

Für die Funktion $ y = \sin(3x + \dfrac{\pi}{3}) $, um einen Zyklus zu durchlaufen, muss der Ausdruck $ 3x + \dfrac{\pi}{3} $ wie folgt sein: \[ 0 \leq 3x + \dfrac{\pi}{3} \leq 2\pi \] Lösen Sie die obige Ungleichung nach $ x $ auf, um das Intervall zu erhalten, das einer Periode entspricht. \[ -\dfrac{\pi}{9} \leq x \leq \dfrac{5\pi}{9} \] Finden Sie die Mittelwerte wie in Beispiel 6 und vervollständigen Sie die Wertetabelle.

$Werte von y =\sin(3 x + pi/3)$

Der Graph der gegebenen Funktion $ y =\sin(3 x + \dfrac{\pi}{3}) $ (blau) wird mit dem Graphen von $\sin(3 x) $ (rot) verglichen. Sie sind ähnlich, bis auf die Verschiebung um $ \dfrac{\pi}{9} $ nach links.

Graph von y = sin(3x + pi/3) — Abbildung 8. Graph von $ y = \sin(3x + \dfrac{\pi}{3}) $

Graph der Funktion: $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $

Beispiel 8

Finden Sie den Wertebereich, die Periode und die Phasenverschiebung der Funktion $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $ und zeichnen Sie sie.

Lösung zu Beispiel 8

Wir wissen, dass der Wertebereich von $ \sin(2x - \pi/5) $ durch das Intervall $[-1 , 1]$ gegeben ist, oder als Ungleichung schreiben wir: \[ -1 \leq \sin(2x - \pi/5) \leq 1 \] Multiplizieren Sie alle Terme der Ungleichung mit $-2$ und ändern Sie die Ungleichheitszeichen: \[ 2 \geq -2\sin(2x - \pi/5) \geq -2 \] Addieren Sie $+1$ zu allen Termen der Ungleichung und schreiben Sie um als: \[ -2 + 1 \leq -2\sin(2x - \pi/5) + 1 \leq 2 + 1 \] Was den Wertebereich der gegebenen Funktion ergibt als: \[ -1 \leq -2\sin(2x - \pi/5) + 1 \leq 3 \] Im Allgemeinen ist der Wertebereich der Funktion $ y = a\sin(bx + c) + d $ oder $ y = a\cos(bx + c) + d $ gegeben durch das Intervall: \[ [ -|a| + d , |a| + d ] \quad \text{oder in Ungleichungsform} \quad -|a| + d \leq y \leq |a| + d \] Die Periode ist gegeben durch: \[ \dfrac{2\pi}{|b|} = \dfrac{2\pi}{|2|} = \pi \] Die Phasenverschiebung ist gegeben durch: \[ -\dfrac{c}{b} = -\dfrac{-\pi/5}{2} = \dfrac{\pi}{10} \] Um $ y = -2\sin(2x - \pi/5) + 1 $ über eine Periode zu zeichnen, muss der Ausdruck $ 2x - \pi/5 $ einen Zyklus wie folgt durchlaufen: \[ 0 \leq 2x - \pi/5 \leq 2\pi \] Lösen Sie die obige Ungleichung, um zu erhalten: \[ \dfrac{\pi}{10} \leq x \leq \dfrac{11\pi}{10} \] Verwenden Sie den niedrigsten Wert $ \dfrac{\pi}{10} $ und den höchsten Wert $ \dfrac{11\pi}{10} $ in der obigen Ungleichung (die eine Periode ergibt), um eine Wertetabelle zu erstellen, indem Sie die Periode in 4 gleiche Intervalle unterteilen:

$Werte von y = - 2 sin(2 x - \dfrac{\pi}{5}) + 1$

Es ist wichtig zu beachten, dass der Graph über eine Periode in ein Rechteck eingeschrieben ist mit einer Länge von $ \dfrac{\pi}{10} $ bis $ \dfrac{11\pi}{10} $, dem Intervall über eine Periode, das oben durch Lösen der Ungleichung $ 0 \leq (2x - \pi/5) \leq 2\pi $ gefunden wurde, und einer Breite vom Minimum und Maximum (Wertebereich) der Werte von $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $, gleich $ -2 + 1 = -1 $ und $ 2 + 1 = 3 $, was dem bereits in der Tabelle gefundenen Wertebereich entspricht.

Graph von y = -2 sin(2x - π/5) + 1 — Abbildung 9. Graph von $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $

Übung

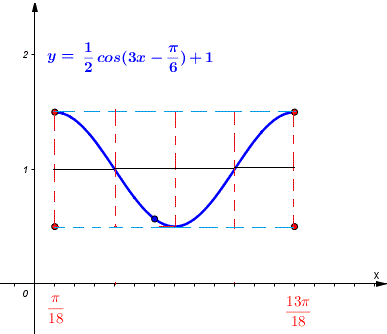
Finden Sie für die unten angegebene Funktion die Start- und End-x-Werte über eine Periode, den Wertebereich und zeichnen Sie sie über eine Periode. \[ y = \dfrac{1}{2} \cos\left(3x - \dfrac{\pi}{6}\right) + 1 \]

Lösungen zur obigen Übung

Eine Periode: $ \dfrac{\pi}{18} \leq x \leq \dfrac{13\pi}{18} $, Wertebereich: $ [1/2 , 3/2] $. Siehe Grafik unten.

Graph von y = (1/2) cos(3x - π/6) + 1 — Abbildung 10. Graph von $ y = \dfrac{1}{2} \cos\left(3x - \dfrac{\pi}{6}\right) + 1 $

Weitere Referenzen und Links

Sinusfunktion Kosinusfunktion
Einheitskreis
Winkel in Normalposition
Wertebereich von sin(x)
Periode trigonometrischer Funktionen
Phasenverschiebung einer Sinusfunktion
Eigenschaften der sechs trigonometrischen Funktionen

Startseite