Fragen zu Logarithmen und Exponentialfunktionen mit Antworten und detaillierten Lösungen für die 11. Klasse werden vorgestellt.
Seiteninhalt
1) Eine der wichtigsten Eigenschaften von Logarithmus- und Exponentialfunktionen ist, dass sie Umkehrfunktionen voneinander sind. Daher können wir exponentielle und logarithmische Ausdrücke mit den folgenden Äquivalenzen umwandeln:
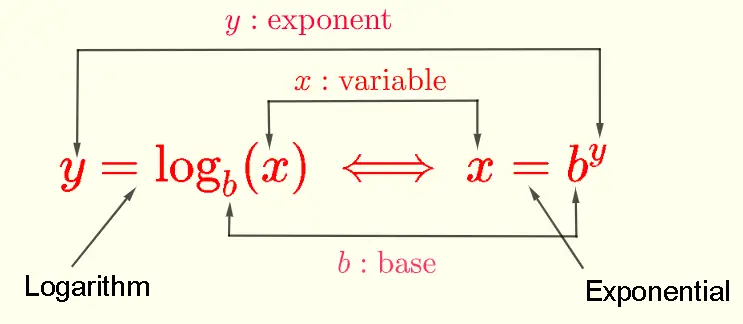
wobei das Symbol \( \iff \) "ist äquivalent zu" bedeutet, \( y \) der Exponent ist, \( b \) die Basis ist, so dass \( b \gt 0 , b \ne 1 \) und \( x \gt 0 \).
Numerisches Beispiel
\[ 2 = \log_3 (9) \iff 9 = 3^2 \]
2) Eineindeutige (injektive) Eigenschaften von Logarithmus- und Exponentialfunktionen
a) Wenn \( \quad b^x = b^y \quad \), dann ist \( \quad x = y \).
b) Wenn \( \quad \log_b (x) = \log_b (y) \quad \), dann ist \( \quad x = y \) , (HINWEIS: Die Logarithmen auf beiden Seiten haben die gleiche Basis).
Verwende die äquivalenten Ausdrücke : \( y = \log_b(x) \iff x = b^y \), um zu schreiben:
a) \( \log_x (a) = c \) als Exponentialausdruck \( a = x^c \)
b) \( \log_b (2x + 1) = 3 \) als Exponentialausdruck \( 2x + 1 = b^3 \)
Verwende die äquivalenten Ausdrücke : \( x = b^y \iff y = \log_b (x) \), um zu schreiben:
a) \( 3^x = m \) als Logarithmus \( x = \log_3 (m) \)
b) \( x^2 = a \) als Logarithmus \( 2 = \log_x (a) \)
Verwende die äquivalenten Ausdrücke : \( y = \log_b(x) \iff x = b^y \), um die folgenden Ausdrücke ohne Taschenrechner auszuwerten:
a)
setze \[ y = \log_2 16 \]
Wandle in die Exponentialform um: \[ 2^y = 16 \]
Nutze die Tatsache, dass \( 16 = 2^4\) ist, um zu schreiben: \[ 2^y = 2^4 \]
Daraus folgt mit der oben angegebenen Eineindeutigkeit der Exponentialfunktion, "Wenn \( 2^y = 2^4 \), dann ist y = 4":
\[ y = \log_2 16 = 4 \]
b)
setze \[ y = \log_3 27 \]
Wandle in die Exponentialform um: \[ 3^y = 27 \]
Nutze die Tatsache, dass \( 27 = 3^3 \) ist, um zu schreiben: \[ 3^y = 3^3 \]
Daraus folgt mit der Eineindeutigkeit: \[ y = 3 \]
Also : \[ y = \log_3 27 = 3 \]
c)
setze \[ y = \log_2 (1/32) \]
Wandle in die Exponentialform um: \[ 2^y = \dfrac{1}{32} \]
Nutze die Tatsache, dass \( \dfrac{1}{32} = \dfrac{1}{2^5} = 2^{-5} \) ist, um zu schreiben: \[ 2^y = 2^{-5} \]
und die Eineindeutigkeit der Exponentialfunktion ergibt: \[ y = -5 \]
Also \[ y = \log_2 (1/32) = -5 \]
d)
setze \[ y = \log_{25} 5 \]
Wandle in die Exponentialform um: \[ 25^y = 5 \]
Nutze die Tatsache, dass \( 5 = \sqrt{25} = 25^{1/2} \) ist, um zu schreiben: \[ 25^y = 25^{1/2} \]
Also \[ y = \log_{25} 5 = 1/2 \]
e)
Setze \( y = \log \sqrt{10} \) (Hinweis: Logarithmus zur Basis 10 ); Wandle in die Exponentialform um: \[ 10^y = \sqrt{10} = 10^{1/2} \]
Also \[ y = \log \sqrt{10} = 1/2 \]
f)
Setze \( y = \log_b 1 \) ; Wandle in die Exponentialform um: \[ b^y = 1 = b^0 \quad \text{daher} \quad y = \log_b 1 = 0 \]
g)
setze \( y = \log_{0.1} 10 \) ; Wandle in die Exponentialform um: \[ 0.1^y = 10 \]
Nutze \( 10 = 1 / 0.1 = 0.1^{-1} \) , also \[ 0.1^y = 0.1^{-1} \quad \text{ was ergibt} \quad y = \log_{0.1} 10 = - 1 \]
Verwende die äquivalenten Ausdrücke : \( y = \log_b(x) \iff x = b^y \), um die folgenden logarithmischen Gleichungen nach \( x \) aufzulösen:
a)
\( \log_2 x = 3 \) ; Wandle in die Exponentialform um: \[ x = 2^3 = 8 \]
b)
\( \log_x 8 = 3 \) ; Wandle in die Exponentialform um: \[ 8 = x^3 \] Schreibe 8 als \[ 8 = 2^3 = x^3\] also \[ x = 2 \]
c)
\( \log_3 x = 1 \) ; Wandle in die Exponentialform um: \[ x = 3^1 = 3 \]
d)
\( \log_{5.6} x = 0 \) ; Wandle in die Exponentialform um: \[ x = 5.6^0 = 1 \]
e)
\( \log_2 (3x + 1) = 4 \) ; Wandle in die Exponentialform um: \[ 3x + 1 = 2^4 = 16 \] Löse nach x auf: \[ 3x + 1 = 16 , 3x = 15 , x = 5 \]
f)
\( \log_3 \dfrac{1}{x+1} = 2 \) ; Wandle in die Exponentialform um: \[ \dfrac{1}{x+1} = 3^2 = 9 \] Löse nach x auf: \[ 1 = 9 (x + 1) , x = - 8 / 9 \]
g)
\( \log_4 \dfrac{x+1}{2x-1} = 0 \) ; Wandle in die Exponentialform um: \[ \dfrac{x+1}{2x-1} = 4^0 = 1 \] Löse nach x auf: \[ x + 1 = 2x - 1 , x = 2 \]
h)
\( \log ( 1/x + 1 ) = 2 \) ; Wandle in die Exponentialform um: \[ 1/x + 1 = 10^2 = 100 \] Löse nach x auf: \[ 1/x + 1 = 100 , 1/x = 99 , x = 1/99 \]
i)
\( \log_x 0.0001 = 4 \) ; Wandle in die Exponentialform um: \[ x^4 = 0.0001 = 1/10000 = 1/10^4 = (1/10)^4 \]
Daraus folgt \[ x^4 = (1/10)^4 \]
Also \[ x = 1/10 \].
Verwende die Eineindeutigkeit: wenn \( b^x = b^y \) dann ist \( x = y \), um die Exponentialgleichungen zu lösen:
Hinweis: In der obigen Gleichung sind die Basen der beiden Exponentialausdrücke beide gleich \( b \).
a)
\( 3^x = 9 = 3^2 \) also \[ x = 2 \]
b)
\( 4^{2x + 1} = 16 = 4^2 \), woraus folgt \[ 4^{2x + 1} = 4^2 \] also \[ 2x + 1 = 2 , x = 1 / 2 \]
c)
\( \left(\dfrac{1}{2} \right)^x = 2 \)
Schreibe \( 2 \) als \( 2 = \left(\dfrac{1}{2} \right)^{-1} \)
woraus folgt \[ \left(\dfrac{1}{2} \right)^x = \left(\dfrac{1}{2} \right)^{-1} \]
also \[ x = - 1 \]
d)
\( 10^x = 5 \) , wandle den Exponentialausdruck in einen Logarithmus zur Basis 10 um: \[ \quad x = \log_{10} 5 \]
e)
\( \left(\dfrac{1}{3} \right)^{x/2 - 2} = 9 = 3^2 \).
Schreibe \( 3^2 \) als \[ \left(\dfrac{1}{3} \right)^{-2} \]
woraus folgt \[ \left(\dfrac{1}{3} \right)^{x/2 - 2} = \left(\dfrac{1}{3} \right)^{-2} \].
Also \[ x/2 - 2 = - 2 \]
löse, um zu erhalten: \[ x = 0 \]
f)
\( 0.01^x = 100 \). Schreibe:
\[ 100 = \dfrac{1}{0.01} = 0.01^{-1} \quad \text{was ergibt} \quad 0.01^x = 0.01^{-1} \]
also \[ x = -1 \]
g)
Gegeben ist die Gleichung: \[ 2^{2x} - 6 \cdot 2^x = - 8 \]
Beachte, dass \[ 2^{2x} = (2^x)^2 \] ist.
Setze \( u = 2^x \) und schreibe \[ u^2 = (2^x)^2 = 2^{2x} \]
Wir ersetzen nun \( 2^x \) durch \( u \) und \( 2^{2x} \) durch \( u^2 \) in der gegebenen Gleichung und schreiben die Gleichung nur in Termen von \( u \) und in Standardform wie folgt um:
\[ u^2 - 6 u + 8 = 0 \]
Löse die obige quadratische Gleichung durch Faktorisieren:
\[ (u - 2)(u - 4) = 0 \]
Lösungen in u: \[ u = 2 \quad \text{und} \quad u = 4 \]
Wir lösen nun nach \( x \) auf, indem wir die oben vorgenommene Substitution verwenden:
\[ u = 2 = 2^x \quad \text{ergibt die Lösung:} \quad x = 1 \]
\[ u = 4 = 2^x = 2^2 \quad \text{ergibt die Lösung:} \quad x = 2 \]