Convert Logarithms and Exponentials
Relationship Between Exponential and Logarithm
The logarithmic functions
and the exponential functions 
are inverse of each other, hence
where \( b \) is the common base of the exponential and the logarithm.
The above equivalence helps in solving logarithmic and exponential functions and needs a deep understanding. Examples, of how the above relationship between the logarithm and exponential may be used to transform expressions and solve problems are presented below.
Example 1
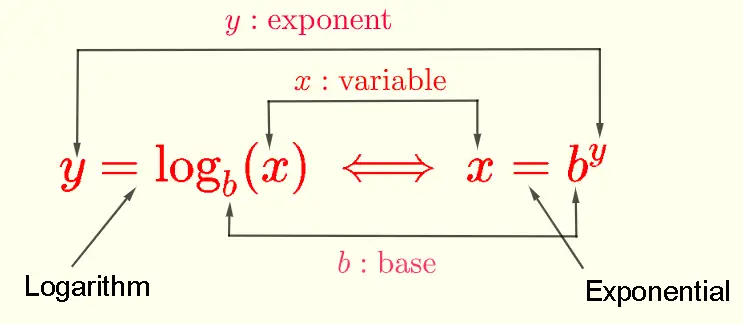
Change each logarithmic expression to an exponential expression.
1. \( \log_3 27 = 3 \)
2. \( \log_{36} 6 = 1 / 2 \)
3. \( \log_2 (1 / 8) = -3 \)
4. \( \log_8 2 = 1 / 3 \)
Solution to Example 1:
1. The logarithmic form \( \log_3 27 = 3 \) is equivalent to the exponential form
\[ 27 = 3^3 \]
2. The logarithmic expression \( \log_{36} 6 = 1 / 2 \) is equivalent to the exponential expression
\[ 6 = 36^{1/2} \]
3. The expression \( \log_2 (1 / 8) = - 3 \) in exponential form is given by
\[ 1 / 8 = 2^{-3} \]
4. \( \log_8 2 = 1 / 3 \) in exponential form is given by
\[ 2 = 8^{1/3} \]
Example 2
Change each exponential expression to a logarithmic expression.
1. \( 3^4 = 81 \)
2. \( 4^{1/2} = 2 \)
3. \( 3^{-1/3} = 1 / 27 \)
4. \( 10^3 = 1000 \)
Solution to Example 2:
1. The exponential form \( 3^4 = 81 \) is equivalent to the logarithmic form
\[ 4 = \log_3 (81) \]
2. The exponential form \( 4^{1/2} = 2 \) is equivalent to the logarithmic form
\[ 1 / 2 = \log_4 2 \]
3. \( 3^{-3} = 1 / 27 \) in logarithmic form is given by
\[ -3 = \log_3 (1/ 27) \]
4. \( 10^3 = 1000 \) in logarithmic form is given by
\[ 3 = \log_{10} 1000 \]
Example 3
Solve for \( x \) the following equations.1. \( \log_3 x = 5 \)
2. \( \log_2 (x - 3) = 2 \)
3. \( 2 \log_3 (- x + 1) = 6 \)
Solution to Example 3:
1. To solve the equation \( \log_3 x = 5 \), rewrite it into exponential form
\[ x = 3^5 \]
2. Rewrite the equation \( \log_2 (x - 3) = 2 \) into exponential form
\[ x - 3 = 2^2 = 4 \]
Solve for x
\[ x = 4 + 3 = 7 \]
3.Divide all terms of the equation \( 2 \log_3 (- x + 1) = 6 \) by 2
\[ \log_3 (- x + 1) = 3 \]
Rewrite the equation obtained in exponential form
\[ - x + 1 = 3^3 = 27 \]
Solve for x
\[ x = - 26 \]
More References and Links Related to the Logarithmic Functions
Logarithm and Exponential Questions with Answers and Solutions
Rules of Logarithms and Exponentials - Questions with Solutions.
