Parabel-Fragen und Probleme mit detaillierten Lösungen
Erkunden Sie eine Sammlung von Parabelproblemen. Detaillierte Lösungen mit Erklärungen werden ebenfalls bereitgestellt, um Ihr Verständnis zu vertiefen.
Aufgabe 1
Finden Sie die x- und y-Achsenabschnitte, den Scheitelpunkt und die Symmetrieachse der Parabel mit der Gleichung \( y = - x^2 + 2 x + 3 \)?
Die x-Achsenabschnitte sind die Schnittpunkte der Parabel mit der x-Achse, das sind Punkte auf der x-Achse, und daher sind ihre y-Koordinaten gleich 0. Daher müssen wir die Gleichung lösen: \[ 0 = - x^2 + 2x + 3 \] Faktorisieren Sie die rechte Seite der Gleichung: \[ -(x - 3)(x + 1) = 0\] Lösen Sie nach x auf, um zu finden: \[ x = 3 \quad \text{und} \quad x = -1\] , Der y-Achsenabschnitt ist der Schnittpunkt der Parabel mit der y-Achse, ein Punkt auf der y-Achse, und daher ist seine x-Koordinate gleich 0. Der y-Achsenabschnitt ist :\( y = - (0)^2 + 2 (0) + 3 = 3 \), Der Scheitelpunkt wird gefunden, indem die Gleichung der Parabel in Scheitelpunktform \(y = a(x - h)^2 + k \) geschrieben wird, indem man die quadratische Ergänzung durchführt und die Koordinaten des Scheitelpunkts \( h \) und \( k \) identifiziert. Quadratische Ergänzung: \[ y = - x^2 + 2 x + 3 = -( x^2 - 2 x - 3) = -( (x - 1)^2 - 1 - 3) = -(x - 1 )^2 + 4 \] Scheitelpunkt am Punkt \[ (1 , 4) \] Sie können alle oben gefundenen Punkte anhand des Graphen von \[ y = - x^2 + 2 x + 3 \] unten überprüfen.

Aufgabe 2
Wie lauten die Schnittpunkte der Geraden mit der Gleichung \( 2x + 3y = 7 \) und der Parabel mit der Gleichung \( y = - 2 x^2 + 2 x + 5\)?
Die Schnittpunkte sind Lösungen des simultanen Gleichungssystems \[ 2x + 3y = 7 \quad \text{und} \quad y = - 2 x^2 + 2 x + 5 \]. Ersetzen Sie \( y \) durch \( - 2 x^2 + 2 x + 5 \) in der Gleichung \( 2x + 3y = 7 \), um zu erhalten \[ 2x + 3(- 2x^2 + 2x + 5) = 7 \] Schreiben Sie die oben erhaltene quadratische Gleichung in Standardform \[ -6x^2 + 8x + 8 = 0 \] Teilen Sie alle Terme der Gleichung durch 2. \[ -3x^2 + 4x + 4 = 0 \] Lösung für x \[ x = 2 \quad , \quad x = -2/3 \] Setzen Sie x für die vorherigen Lösungen in \( 2x + 3y = 7 \) ein, um y zu finden. \[ x = 2 , y = 1 \quad \text{und} \quad x = -\frac{2}{3}, \quad y = \frac{25}{9} \] Die Schnittpunkte sind: \[ (2 , 1) \quad \text{und} \quad (-\frac{2}{3} , \frac{25}{9} ) \]. Überprüfen Sie die Antwort unten grafisch.

Aufgabe 3
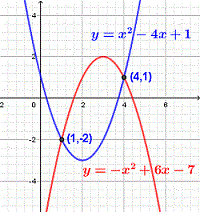
Finden Sie die Schnittpunkte der beiden Parabeln mit den Gleichungen \( y = -(x - 3)^2 + 2\) und \( y = x^2 - 4x + 1\).
Die Schnittpunkte der beiden Parabeln sind Lösungen des simultanen Gleichungssystems
\[ y = -(x - 3)^2 + 2 \quad und \quad y = x^2 - 4x + 1 \].
Ersetzen Sie \( y \) durch \( -(x - 3)^2 + 2 \) in der zweiten Gleichung:
\[ -(x - 3)^2 + 2 = x^2 - 4x + 1 \]
Expandieren, zusammenfassen und in Standardform schreiben
\[ -2x^2 + 10x - 8 = 0 \]
Teilen Sie alle Terme durch \( -2 \)
\[ x^2 - 5x + 4 = 0 \]
Die Lösungen der obigen quadratischen Gleichung sind:
\[ x = 1 \quad und \quad x = 4 \]
Verwenden Sie eine der Gleichungen, um y zu finden:
\( x = 1 \) in die Gleichung \(y = -(x - 3)^2 + 2 \) eingesetzt ergibt \( y = -(1 - 3)^2 + 2 = -2 \)
\( x = 4 \) in die Gleichung \( y = -(x - 3)^2 + 2 \) eingesetzt ergibt \( y = -(4 - 3)^2 + 2 = 1 \)
Schnittpunkte sind: \[ (1 , -2) \quad \text{und} \quad (4 , 1) \] Überprüfen Sie die Antwort unten grafisch.
Aufgabe 4
Finden Sie die Gleichung der Parabel \( y = 2 x^2 + b x + c\), die durch die Punkte \( (-1,-5)\) und \( (2,10)\) verläuft.
Die Punkte \((-1,-5)\) und \((2,10) \) liegen auf dem Graphen der Parabel \( y = 2 x^2 + b x + c\) und sind daher Lösungen der Parabelgleichung. Durch Einsetzen der Koordinaten der beiden Punkte erhalten wir die Gleichungen:
\[ -5 = 2 (-1)^2 + b (-1) + c\]
und
\[10 = 2 (2)^2 + b (2) + c\]
Schreiben Sie das obige System mit den Unbekannten \( b \) und \( c \) in Standardform.
\[ - b + c = - 7\]
\[ 2b + c = 2\]
Lösen Sie das obige Gleichungssystem, um zu erhalten: \( c = - 4 \) und \( b = 3\)
Die Gleichung der Parabel, die durch die Punkte \( (-1,-5)\) und \( (2,10)\) verläuft, ist gegeben durch: \[ y = 2 x^2 + b x + c = 2 x^2 + 3 x - 4\]
Verwenden Sie einen Funktionsplotter, um Ihre Antwort zu überprüfen, indem Sie \( y = 2 x^2 + 3 x - 4 \) grafisch darstellen und prüfen, ob der Graph durch die Punkte \( (-1,-5) \) und \((2,10)\) verläuft.
Aufgabe 5
Wie lautet die Gleichung der Parabel mit x-Achsenabschnitten bei \( x = 2\) und \( x = -3\), und einem y-Achsenabschnitt bei \( y = 5\)?
Die Gleichung einer Parabel mit x-Achsenabschnitten bei \( x = 2 \) und \( x = -3 \) kann als Produkt zweier Faktoren geschrieben werden, deren Nullstellen die x-Achsenabschnitte sind, wie folgt: \[ y = a(x - 2)(x + 3) \] Wir verwenden nun den y-Achsenabschnitt bei (0, 5), einen Punkt, durch den die Parabel verläuft, um zu schreiben: \[ 5 = a(0 - 2)(0 + 3) \] Lösen Sie nach \(a\) auf \[ a = - \dfrac{5}{6} \] Gleichung: \[ y = - \dfrac{5}{6} (x - 2)(x + 3)\] Zeichnen Sie \( y = - \dfrac{5}{6} (x - 2)(x + 3)\) und verifizieren Sie, dass der Graph x-Achsenabschnitte bei \( x = 2 , x = -3 \) und einen y-Achsenabschnitt bei \( y = 5\) hat.
Aufgabe 6
Finden Sie die Gleichung der Parabel \( y = a x^2 + b x + c \), die durch die Punkte \( (0,3) \) , \( (1,-4)\) und \( (-1 , 4)\) verläuft.
Die Punkte \( (0,3), (1,-4) \) und \( (-1,4) \) liegen auf dem Graphen der Parabel \( y = a x^2 + b x + c \) und sind daher Lösungen der Parabelgleichung. Daher schreiben wir das System der 3 Gleichungen wie folgt: \[ (0,3) \Rightarrow c = 3 \quad (I) \] \[ (1,-4) \Rightarrow a + b + 3 = -4 \Rightarrow a + b = -7 \quad (II) \] \[ (-1,4) \Rightarrow a - b + 3 = 4 \Rightarrow a - b = 1 \quad (III) \] Gleichung (I) ergibt: \[ c = 3 \] Setzen Sie 3 für c in die Gleichungen (II) und (III) ein \[ a + b = -7 \] \[ a - b = 1 \] Lösen Sie das System nach \( a \) und \( b \) auf, um zu erhalten \[a = - 3 \; , \; b = - 4 \] Die Gleichung der Parabel ist gegeben durch: \[ y = a x^2 + b x + c = -3 x^2 - 4x + 3 \] Zeichnen Sie die Graphen von \( y = -3 x^2 - 4x + 3 \) und verifizieren Sie, dass der Graph durch die Punkte \( (0,3), (1,-4) \) und \( (-1 ,4) \) verläuft.
Aufgabe 7
Finden Sie die Gleichung der Parabel mit vertikaler Symmetrieachse, die die Gerade \( y = 3 \) bei \( x = -2 \) tangiert und deren Graph durch den Punkt \((0,5) \) verläuft.
Die Gleichung der Parabel mit vertikaler Symmetrieachse hat die Form \( y = a x^2 + b x + c \) oder in Scheitelpunktform \( y = a(x - h)^2 + k \), wobei der Scheitelpunkt am Punkt \( (h , k)\) liegt.
In diesem Fall tangiert sie eine horizontale Gerade \( y = 3 \) bei \( x = -2 \), was bedeutet, dass ihr Scheitelpunkt am Punkt \( (h , k) = (-2 , 3) \) liegt. Daher kann die Gleichung dieser Parabel wie folgt geschrieben werden:
\[ y = a(x - h)^2 + k = a(x - (-2))^2 + 3 = a(x + 2)^2 + 3 \]
Ihr Graph verläuft durch den Punkt \( (0 , 5) \), der die Gleichung erfüllen muss:
\[ 5 = a(0 + 2)^2 + 3 = 4 a+ 3 \]
Lösen Sie das Obige nach \( a \) auf
\[ a = \dfrac{1}{2} \]
Die Gleichung der Parabel ist gegeben durch: \[ y = \dfrac{1}{2}(x + 2)^2 + 3 \]
Skizzieren Sie die Graphen von \( y = \dfrac{1}{2} (x + 2)^2 + 3 \) und verifizieren Sie, dass der Graph die horizontale Gerade \( y = 3 \) bei \( x = -2 \) tangiert und dass der Graph durch den Punkt \( (0 , 5) \) verläuft.
Aufgabe 8
Für welchen Wert der Steigung m ist die Gerade mit der Gleichung \( y = m x - 3 \) tangential zur Parabel mit der Gleichung \( y = 3 x^2 - x \)?
Eine Gerade und eine Parabel sind tangential, wenn sie nur einen Schnittpunkt haben, den Berührungspunkt. Die Schnittpunkte werden durch Lösen des Systems \( y = m x - 3 \quad und \quad y = 3 x^2 - x \) gefunden. Ersetzen Sie \( y \) durch \( m x - 3 \) in der zweiten Gleichung: \[ mx - 3 = 3 x^2 - x \] Schreiben Sie als standardmäßige quadratische Gleichung: \[ 3 x^2 - x(1 + m) + 3 = 0 \] Die Diskriminante der obigen quadratischen Gleichung ist gegeben durch: \[ \Delta = (1 + m)^2 - 4(3)(3) \] Die Gerade ist tangential zur Parabel, wenn sie nur einen Schnittpunkt haben, das heißt wenn: \[\Delta = 0 \] Daher die Gleichung: \[(1 + m)^2 - 4(3)(3) = 0 \] Lösen Sie nach \( m \) auf \[(1 + m)^2 = 36 \] Lösungen sind: \[ m = 5 \quad und \quad m = -7 \] Verwenden Sie einen Funktionsplotter, um Ihre Antwort zu überprüfen, indem Sie die Graphen der Geraden: \( y = 5 x - 3 \) ( \( m = 5 \) Lösung ), \( y = -7 x - 3 \) ( \( m = -7 \) Lösung) und der Parabel \( y = 3 x^2 - x\) zeichnen und prüfen, ob die beiden Geraden den Graphen der Parabel \( y = 3 x^2 - x\) tangieren.
Aufgabe 9
Für welche Werte des Parameters \( b \) schneidet die Gerade mit der Gleichung \( y = 2 x + b \) die Parabel mit der Gleichung \( y = - x^2 - 2 x + 1\) an zwei verschiedenen Punkten?
Die Schnittpunkte werden durch Lösen des Systems \[ y = 2 x + b \quad und \quad y = - x^2 - 2x + 1 \] gefunden. Ersetzen Sie \( y \) durch \( 2 x + b \) in der zweiten Gleichung \[ 2x + b = - x^2 - 2x + 1 \] Schreiben Sie als standardmäßige quadratische Gleichung: \[ - x^2 - 4x + 1 - b = 0 \] Die Diskriminante der obigen Gleichung ist gegeben durch: \[ \Delta = (-4)^2 - 4(-1)(1 - b) = 20 - 4b \] Die Graphen von \( y = 2 x + b \) und \( y = - x^2 - 2 x + 1 \) haben zwei Schnittpunkte, wenn \( \Delta \gt 0 \) (Fall von zwei reellen Lösungen einer quadratischen Gleichung), daher die Ungleichung \[ 20 - 4 b \gt 0 \] Lösen Sie nach \( b \) auf \[ b \lt 5 \] Verwenden Sie einen Funktionsplotter, um Ihre Antwort zu überprüfen, indem Sie Graphen von \( y = - x^2 - 2 x + 1 \) und Geraden durch Gleichungen \( y = 2 x + b \) für Werte von \( b \gt 5 \) , \( b \lt 5 \) und \( b = 5 \) zeichnen, um zu sehen, wie viele Schnittpunkte der Parabel und der Geraden es für jeden dieser Werte von \( b \) gibt.
Aufgabe 10
Finden Sie die Gleichung \( y = a x^2 + x \) der Parabel, die die Gerade mit der Gleichung \( y = 3 x + 1\) tangiert.
Die Schnittpunkte werden durch Lösen des Systems \[ y = a x^2 + x \quad und \quad y = 3 x + 1 \] gefunden. Ersetzen Sie \( y \) durch \( 3 x + 1 \) in der Gleichung \( y = a x^2 + x \) \[ 3 x + 1 = a x^2 + x \] Schreiben Sie als standardmäßige quadratische Gleichung: \[ a x^2 - 2 x - 1 = 0 \] Diskriminante der quadratischen Gleichung: \[ \Delta = (-2)^2 - 4(a)(-1) = 4 + 4 a \] Die Graphen sind tangential, wenn sie einen Schnittpunkt haben (Fall einer Lösung einer quadratischen Gleichung), wenn \( \Delta = 0 \). Daher \[ 4 + 4 a = 0 \] Lösen Sie nach \(a\) auf \[ a = -1 \] Parabelgleichung: \[ y = -x^2 + x \] Zeichnen Sie \( y = - x^2 + x \) und \( y = 3 x + 1 \), um die obige Antwort zu überprüfen.
Aufgabe 11
Verschieben Sie den Graphen der Parabel \( y = x^2 \) um 3 Einheiten nach links, spiegeln Sie dann den resultierenden Graphen an der x-Achse und verschieben Sie ihn dann um 4 Einheiten nach oben. Wie lautet die Gleichung der neuen Parabel nach diesen Transformationen?
Beginnen Sie mit: \[ y = x^2 \] Verschiebung um 3 Einheiten nach links: \[ y = (x + 3)^2 \] Spiegelung an der x-Achse: \[ y = -(x + 3)^2 \] Verschiebung um 4 Einheiten nach oben: \[ y = -(x + 3)^2 + 4 \]
Aufgabe 12
Welche Transformationen sind notwendig, um den Graphen der Parabel \( y = x^2 \) in den Graphen der Parabel \( y = - x^2 + 4 x + 6 \) zu überführen?
Gegeben: \[ y = - x^2 + 4 x + 6 \] Durch quadratische Ergänzung in Scheitelpunktform umschreiben: \[ y = - x^2 + 4 x + 6 = - (x - 2)^2 + 10\] Beginnend: \[ y = x^2\] Verschiebung um 2 Einheiten nach rechts: \[ y = (x - 2)^2\] Spiegelung an der x-Achse: \[ y = -(x - 2)^2 \] Verschiebung um 10 Einheiten nach oben: \[ y = -(x - 2)^2 + 10 \]
Aufgabe 13
Schreiben Sie die Gleichung der Parabel, die im Graphen unten dargestellt ist.

Jeder im gegebenen Graphen identifizierte Punkt kann verwendet werden, um die Gleichung der Parabel zu finden. Die Verwendung der \( x \)- und \( y \)-Achsenabschnitte und des Scheitelpunkts sind jedoch bessere Wege, um die Gleichung der Parabel zu finden, deren Graph unten gezeigt wird.
Zwei Methoden werden zur Lösung des Problems vorgestellt:
Methode 1:
Der Graph hat zwei x-Achsenabschnitte: (-5, 0) und (-1, 0)
Verwenden Sie die zwei x-Achsenabschnitte bei (-5, 0) und (-1, 0), um die Gleichung der Parabel als Produkt von zwei linearen Faktoren zu schreiben:
\[ y = a(x + 1)(x + 5)\]
Verwenden Sie den y-Achsenabschnitt bei (0, -5), um zu schreiben
\[ - 5 = a(0 + 1)(0 + 5) = 5 a\]
Lösen Sie nach \(a \) auf
\[ a = -1 \]
Schreiben Sie die Gleichung der Parabel:
\[ y = -(x + 1)(x + 5) = - x^2 - 6 x - 5 \]
Methode 2:
Verwenden Sie den Scheitelpunkt bei \( ( h , k) = (-3 , 4) \), um die Gleichung der Parabel in Scheitelpunktform wie folgt zu schreiben: \[ y = a(x - h)^2 + k = a(x + 3)^2 + 4 \] Verwenden Sie den y-Achsenabschnitt (0, -5), um \(a\) zu finden. \[ - 5 = a(0 + 3)^2 + 4 \] Lösen Sie das Obige nach \(a\) auf: \[ a = -1 \] Die Gleichung der Parabel ist gegeben durch \[ y = -(x + 3)^2 + 4 = - x^2 -6 x - 5 \]
Weitere Referenzen und Links
- Hochschulalgebra-Probleme mit Antworten - Beispiel 9: Gleichung von Parabeln.
- Parabelproblem mit Lösung.
- Scheitelpunkt-Achsenabschnitt Parabelprobleme.
- Finden Sie die Schnittpunkte einer Parabel mit einer Geraden.
- Mathematik der Oberstufe (Klassen 10, 11 und 12) - Kostenlose Fragen und Probleme mit Antworten
- Mathematik der Mittelstufe (Klassen 6, 7, 8, 9) - Kostenlose Fragen und Probleme mit Antworten
- Grundschulmathematik (Klassen 4 und 5) mit kostenlosen Fragen und Problemen mit Antworten
- Homepage