
Suchen Sie nach Möglichkeiten, Exponentialgleichungen zu meistern? Dieser Leitfaden bietet Schülern der 12. Klasse klare, detaillierte Lösungen unter Verwendung sowohl analytischer als auch grafischer Methoden. Sie lernen leistungsstarke Techniken wie Substitution und die Regeln von Exponential- und Logarithmusfunktionen kennen, um komplexe Gleichungen sicher zu lösen.
Wir zeigen auch, wie man Exponentialgleichungen grafisch löst. Dazu schreiben wir die Gleichung zunächst in der Form \( f(x) - g(x) = 0 \) um. Dann zeichnen wir den Graphen der Funktion \( f(x) - g(x) \), und die x-Achsen-Schnittpunkte des Graphen stellen die Lösungen der ursprünglichen Gleichung dar.
Egal, ob Sie sich auf Prüfungen vorbereiten oder einfach nur Ihre mathematischen Fähigkeiten stärken möchten, diese Ressource hilft Ihnen, Exponentialgleichungen Schritt für Schritt zu verstehen und zu lösen.
Beachten Sie, dass 27, 9 und 3 als Potenzen von 3 geschrieben werden können:
\[ 27 = 3^3, \quad 9 = 3^2, \quad \text{und} \quad 3 = 3^1 \]Unter Verwendung des Obigen und auch der Formel für negative Exponenten
\[ \dfrac{1}{x^n} = x^{-1} \]Wir schreiben die gegebene Gleichung wie folgt um:
\[ (3^3)^{2x} \cdot (3^{-2})^{x - 2} = (3^2)^{-x} \cdot (3^{-1})^{2 - x} \]Wir verwenden nun die Formel \((x^m)^n = x^{mn}\), um die obige Gleichung wie folgt umzuschreiben.
\[ 3^{6x} \cdot 3^{-2x + 4} = 3^{-2x} \cdot 3^{-2 + x} \]Verwenden Sie die Formel \(x^m \cdot x^n = x^{m + n}\), um die Gleichung wie folgt umzuschreiben
\[ 3^{6x - 2x + 4} = 3^{-2x - 2 + x} \]Vereinfachen Sie die Exponenten, um zu erhalten
\[ 3^{4x + 4} = 3^{-x - 2} \]Wir nutzen die Tatsache, dass eine Exponentialfunktion der Form \(a^x\) eine eineindeutige Funktion ist, was bedeutet, dass wenn \(3^m = 3^n\), dann \(m = n\), um eine algebraische Gleichung unter Verwendung der obigen Gleichung zu schreiben:
\[ 4x + 4 = -x - 2 \]Lösen Sie das Obige nach \(x\) auf, um die Lösung der gegebenen Gleichung zu erhalten.
\[ 5x = -6 \quad \text{ergibt die Lösung} \quad x = \dfrac{-6}{5} = -1.2 \] Nachfolgend ist der Graph der linken Seite der gegebenen Gleichung dargestellt, wenn sie mit der rechten Seite gleich Null wie folgt geschrieben wird: \[ 27^{2x} \left(\dfrac{1}{9}\right)^{x-2} - 9^{-x} \left(\dfrac{1}{x}\right)^{2-x} = 0 \] Der x-Achsen-Schnittpunkt ist eine Näherung für die oben gefundene analytische Lösung. Überprüfen Sie, ob sie wertmäßig nahe beieinander liegen.
Beachten Sie, dass \( \sqrt{16^x} = (16^x)^{1/2} = 16^{(1/2)x} \) ist, und verwenden Sie dies, um die gegebene Gleichung wie folgt umzuschreiben
\[ 16^{(1/2)x} = \left(\dfrac{1}{2}\right)^{x^2 - 1} \]Beachten Sie, dass \( \dfrac{1}{2} = 2^{-1} \) und \( 16 = 2^4 \) ist, und verwenden Sie dies, um die obige Gleichung wie folgt umzuschreiben
\[ (2^4)^{(1/2)x} = (2^{-1})^{x^2 - 1} \]Verwenden Sie die Formel \( (x^m)^n = x^{mn} \), um die obige Gleichung umzuschreiben als
\[ 2^{2x} = 2^{-x^2 + 1} \]Wir verwenden die Tatsache, dass eine Exponentialfunktion der Form \( a^x \) eine eineindeutige Funktion ist, um zu schreiben
\[ 2x = -x^2 + 1 \]Schreiben Sie in Standardform um und lösen Sie die obige quadratische Gleichung.
\[ x^2 + 2x - 1 = 0 \] \[ \Delta = 2^2 - 4(1)(-1) = 8 \]Zwei Lösungen: \( x_1 = -1 - \sqrt{2} \approx -2.41 \) und \( x_2 = -1 + \sqrt{2} \approx 0.41 \)
Der Graph der linken Seite der gegebenen Gleichung, wenn sie mit der rechten Seite gleich Null wie folgt geschrieben wird:
\[ \sqrt{16^x} - \left( \dfrac{1}{2} \right)^{x^2-1} = 0 \]ist unten dargestellt. Die x-Achsen-Schnittpunkte sind Näherungen für die oben gefundenen analytischen Lösungen. Überprüfen Sie, ob sie nahe Werte haben.

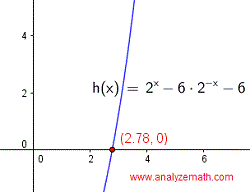
Was sind die Lösungen der Gleichung \[ 2^x - 6 \cdot 2^{-x} = 6 \;\; ? \]
Setze \( u = 2^x \), was auch \( \dfrac{1}{u} = 2^{-x} \) ergibt, und schreibe die Gleichung in Bezug auf \( u \) um.
\[ u - \dfrac{6}{u} = 6 \]\( u \) kann nicht Null sein (weil \( 2^x \) nicht kleiner oder gleich Null sein kann ), daher multiplizieren wir alle Terme der obigen Gleichung mit \( u \) und vereinfachen.
\[ u \left( u - \dfrac{6}{u} \right) = 6u \] \[ u^2 - 6 = 6u \] \[ u^2 - 6u - 6 = 0 \]Lösen Sie die obige quadratische Gleichung nach \( u \), um zwei Lösungen zu erhalten:
\[ u_1 = 3 + \sqrt{15} \quad \text{und} \quad u_2 = 3 - \sqrt{15} \]Wir lösen nun nach \( x \) unter Verwendung der obigen Substitution \( u = 2^x \).
Erste Gleichung: \( 2^x = 3 + \sqrt{15} \)
\[ \ln(2^x) = \ln(3 + \sqrt{15}) \] \[ x \ln(2) = \ln(3 + \sqrt{15}) \] \[ x = \dfrac{\ln(3 + \sqrt{15})}{\ln 2} \approx 2.78 \]Zweite Gleichung: \( 2^x = 3 - \sqrt{15} \) hat keine Lösung, da \( 3 - \sqrt{15} \) kleiner als Null ist.
Nachfolgend ist der Graph der linken Seite der gegebenen Gleichung dargestellt, wenn sie mit der rechten Seite gleich Null wie folgt geschrieben wird: \( 2^x - 6 \cdot 2^{-x} - 6 = 0 \). Der \( x \)-Achsen-Schnittpunkt ist eine Näherung für die Lösung der oben gefundenen analytischen Lösung.
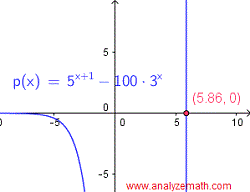
Finden Sie die Lösungen der Gleichung \[ 5^{x+1} = 100 \cdot 3^x \]
Nehmen Sie den natürlichen Logarithmus (\ln) beider Seiten der gegebenen Gleichung:
\[ \ln(5^{x + 1}) = \ln(100 \cdot 3^x) \]Verwenden Sie Logarithmusregeln zur Vereinfachung.
\[ (x + 1) \ln 5 = \ln 100 + x \ln 3 \]Multiplizieren Sie die linke Seite aus und gruppieren Sie Terme mit x
\[ x \ln 5 + \ln 5 = \ln 100 + x \ln 3 \] \[ x (\ln 5 - \ln 3) = \ln 100 - \ln 5 \]Lösen Sie nach \(x \) auf.
\[ x = \dfrac{\ln 100 - \ln 5}{\ln 5 - \ln 3} \approx 5.86 \]Nachfolgend ist der Graph der linken Seite der gegebenen Gleichung dargestellt, wenn sie mit der rechten Seite gleich Null wie folgt geschrieben wird:
\[ 5^{x+1} - 100 \cdot 3^x = 0 \]Der x-Achsen-Schnittpunkt ist eine Näherung für die Lösung der oben gefundenen analytischen Lösung.
Lösen Sie die Gleichung \[ \dfrac{e^x - e^{-x}}{2} = 3 \]
Setze \( u = e^x \), was auch \( \dfrac{1}{u} = e^{-x} \) ergibt, und schreibe die Gleichung in \( u \) um. \( u = e^x \) kann nicht kleiner oder gleich Null sein.
\[ \dfrac{u - \dfrac{1}{u}}{2} = 3 \]Multiplizieren Sie beide Seiten mit 2 und vereinfachen Sie:
\[ u - \dfrac{1}{u} = 6 \]Multiplizieren Sie beide Seiten mit \( u \) und vereinfachen Sie:
\[ u^2 - 1 = 6u \] \[ u^2 - 6u - 1 = 0 \]Lösen Sie nach \( u \) auf, um zwei Lösungen zu erhalten:
\[ u_1 = 3 + \sqrt{10} \quad \text{und} \quad u_2 = 3 - \sqrt{10} \]Wir lösen nun nach \( x \) unter Verwendung der obigen Substitution \( u = e^x \).
Erste Gleichung: \[ e^x = 3 + \sqrt{10} \] Nehmen Sie den \( \ln \) beider Seiten: \[ \ln(e^x) = \ln(3 + \sqrt{10}) \]Vereinfachen Sie, um zu lösen:
\[ x = \ln(3 + \sqrt{10}) \approx 1.82 \]Zweite Gleichung: \( e^x = 3 - \sqrt{10} \) hat keine Lösung, da \( 3 - \sqrt{10} \) kleiner als Null ist.
Nachfolgend ist der Graph der linken Seite der gegebenen Gleichung dargestellt, wenn sie mit der rechten Seite gleich Null wie folgt geschrieben wird:
\[ \dfrac{e^x - e^{-x}}{2} - 3 = 0 \] Der x-Achsen-Schnittpunkt ist eine Näherung für die Lösung der oben gefundenen analytischen Lösung.
Was sind die Lösungen der Gleichung \[ 3^{2-3x} = 4^{2x+1} \; \; ?\]
Nehmen Sie den natürlichen Logarithmus (ln) beider Seiten
\[ \ln(3^{2 - 3x}) = \ln(4^{2x + 1}) \]Verwenden Sie Logarithmusregeln zur Vereinfachung.
\[ (2 - 3x)\ln 3 = (2x + 1)\ln 4 \]Multiplizieren Sie beide Seiten der Gleichung aus und gruppieren Sie Terme mit \( x \).
\[ 2\ln 3 - 3x\ln 3 = 2x\ln 4 + \ln 4 \] \[ x(-3\ln 3 - 2\ln 4) = \ln 4 - 2\ln 3 \] \[ x = \dfrac{2\ln 3 - \ln 4}{3\ln 3 + 2\ln 4} \approx 0.13 \]Nehmen Sie den natürlichen Logarithmus (ln) beider Seiten
\[ \ln(3^{2 - 3x}) = \ln(4^{2x + 1}) \]Verwenden Sie Logarithmusregeln zur Vereinfachung.
\[ (2 - 3x)\ln 3 = (2x + 1)\ln 4 \]Multiplizieren Sie beide Seiten der Gleichung aus und gruppieren Sie Terme mit \( x \).
\[ 2\ln 3 - 3x\ln 3 = 2x\ln 4 + \ln 4 \] \[ x(-3\ln 3 - 2\ln 4) = \ln 4 - 2\ln 3 \] \[ x = \dfrac{2\ln 3 - \ln 4}{3\ln 3 + 2\ln 4} \approx 0.13 \]
Beachten Sie, dass
\[ 9^x = (3^2)^x = 3^{2x} = (3^x)^2 \]Schreiben Sie die gegebene Gleichung um unter Verwendung von \( 9^x = (3^x)^2 \) und auch \( 3^{x + 1} = 3 \cdot 3^x \)
\[ (3^x)^2 - 3 \cdot 3^x + 2 = 0 \]Setze \( u = 3^x \) und schreibe die Gleichung in \( u \) um.
\[ u^2 - 3u + 2 = 0 \]Lösen Sie nach \( u \) durch Faktorisieren
\[ (u - 2)(u - 1) = 0 \]Zwei Lösungen: \( u_1 = 2 \) und \( u_2 = 1 \)
Wir lösen nun nach \( x \) unter Verwendung der obigen Substitution \( u = 3^x \).
Erste Gleichung: \( 3^x = 2 \)
\[ \ln(3^x) = \ln 2 \] \[ x \ln 3 = \ln 2 \] \[ x = \dfrac{\ln 2}{\ln 3} \approx 0.63 \]Zweite Gleichung: \( 3^x = 1 \), Lösung \( x = 0 \).
