Die Standardabweichung ist ein Maß dafür, wie nahe die Datenwerte in einem Datensatz am Mittelwert liegen. Es handelt sich um eine kleine Menge, wenn die Daten nahe am Mittelwert verteilt sind, und groß, wenn die Daten weit vom mittlere.
sei x1, x2, x3 ... xN ein Datensatz mit einem Mittelwert μ sein. Um zu messen, wie weit ein Datenwert xi vom Mittelwert entfernt ist, können wir die Differenz d verwenden i gegeben von di = xi - μ
Das Problem mit der obigen Definition besteht darin, dass di negativ oder positiv sein kann und wenn Sie alle d< hinzufügen sub>i für alle Datenwerte, um einen Durchschnitt zu erhalten, können sie sich gegenseitig aufheben. Daher quadrieren wir di, mitteln sie und ziehen dann die Quadratwurzel.
Die Standardabweichung σ einer Population mit N Elementen ist definiert durch
In einer statistischen Studie haben wir möglicherweise große Populationen und daher kann die Berechnung der Standardabweichung für die gesamte Population kostspielig und zeitaufwändig sein. Daher besteht die Idee, Stichproben aus der Population zu verwenden, um die Standardabweichung zu schätzen.
Die Standardabweichung s eines Datensatzes einer Stichprobe mit N Elementen ist definiert durch
Der Hauptunterschied zwischen den beiden Formeln besteht in der Division durch N und N – 1. Wir verwenden N – 1 in der Formel der Standardabweichung für Stichproben, um die Tatsache auszugleichen, dass die Anzahl der Datenwerte in einer Grundgesamtheit groß ist größer als die Anzahl der Datenwerte in einer Stichprobe. Beachten Sie auch, dass die beiden Formeln für sehr großes N sehr nahe beieinander liegende Werte liefern würden.
Ein Online-Rechner zur Berechnung der Standardabweichung ist im Lieferumfang enthalten.
Beispiele zur Standardabweichung
Beispiel 1
Nachfolgend sind drei Datensätze aufgeführt, die drei Populationen repräsentieren.
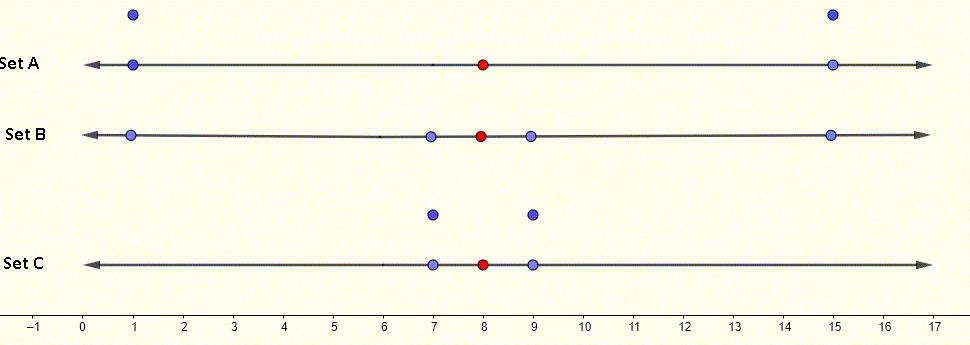
A:{1,1,15,15} B:{1,7,9,15} C:{7,7,9,9}
Berechnen Sie den Mittelwert und die Standardabweichung für jeden Datensatz. Vergleichen Sie die Mittelwerte und die Standardabweichung der drei Sätze. Lösung zu Beispiel 1
Für Satz A
\[\mu_A = \dfrac{1 + 1 + 15 + 15 + 11}{4} = 8\]
\[\sigma_A=\sqrt {\dfrac{(1 - 8)^2 + (1 - 8)^2 + (15 - 8)^2 + (15 - 8)^2}{4}} = 7\]
Für Set B
\[\mu_B = \dfrac{1 + 7 + 9 + 15}{5} = 8\]
\[\sigma_B =\sqrt {\dfrac{(1 - 8)^2 + (7 - 8)^2 + (9 - 8)^2 + (15 - 8)^2}{4}} = 5\]
Für Menge C
\[\mu_C = \dfrac{7 + 7 + 9 + 9}{4} = 8\]
\[\sigma_C =\sqrt {\dfrac{(7 - 8)^2 + (7 - 8)^2 + (9 - 8)^2 + (9 - 8)^2}{4}} = 1\]
Die Mittelwerte der drei Sätze sind gleich 8 (roter Punkt im Diagramm) und die Standardabweichungen sind unterschiedlich. Wir können auf den Diagrammen auf den Zahlenlinien unten die drei Sätze sehen. Es ist grafisch deutlich zu erkennen, dass die Datenwerte in Satz C nahe am Mittelwert liegen und dieser Satz daher die kleinste Standardabweichung aufweist. Die Diagramme auf der Zahlenlinie von Satz A und B zeigen, dass die Daten in Satz A stärker gestreut sind als die Daten in Satz B, daher ist die Standardabweichung für Satz A größer als für Satz B.
Beispiel 2
Unten sind zwei Datensätze aufgeführt, die zwei Populationen repräsentieren.
A:{2, 3, 5, 8, 10} B:{3 , 4 , 6 , 9 , 11}
Berechnen Sie den Mittelwert und die Standardabweichung für jeden Datensatz. Vergleichen Sie die Mittelwerte und die Standardabweichung der beiden Sätze. Lösung für Beispiel 2
Für Satz A
\[\mu_A = \dfrac{2 + 3 + 5 + 8 + 10}{5} = 5,6\]
\[\sigma_A=\sqrt{\dfrac{(2 - 5.6)^2 + (3 - 5.6)^2 + (5 - 5.6)^2 + (8 - 5.6)^2 + (10 - 5.6)^2}{5}}\]
\[=3.0\]
Für Set B
\[\mu_B = \dfrac{3 + 4 + 6 + 9 + 11}{5} = 6,6\]
\[\sigma_B =\sqrt {\dfrac{(2 - 5,6)^2 + (3 - 5,6)^2 + (5 - 5,6)^2 + (8 - 5,6)^2 + (10 - 5,6)^2 }{5}} \]
=3.0
Die Mittelwerte sind unterschiedlich und die Standardabweichung ist gleich. Dies bedeutet, dass die Datenwerte in den beiden Sätzen auf die gleiche Weise um den Mittelwert verteilt sind. Die beiden Mengen A und B werden unten auf Zahlenlinien dargestellt. Obwohl die beiden Sätze unterschiedlich sind, sind die Abstände zwischen den Datenwerten und dem Mittelwert entsprechend gleich und das erklärt, warum die beiden Sätze gleiche Standardabweichungen aufweisen.
Beispiel 3
Die Ergebnisse einer Physikprüfung von Schülern der beiden Klassen A und B weisen die folgenden Mittelwerte und Standardabweichungen auf.
Klasse A: Mittelwert = 78 und Standardabweichung = 5
Klasse A: Mittelwert = 78 und Standardabweichung = 15
Welche Schlussfolgerungen können wir über die Leistungen der Schüler in den beiden Klassen ziehen? Lösung zu Beispiel 3
Die Ergebnisse der beiden Klassen weisen gleiche Mittelwerte auf, aber die Standardabweichung von Klasse B ist höher als die Standardabweichung von Klasse A. Dies bedeutet, dass die Ergebnisse in Klasse B stärker gestreut sind und daher in Klasse B und daher einige Schüler möglicherweise mehr Punkte erzielt haben niedriger als der Durchschnitt, während andere Schüler möglicherweise viel mehr als der Durchschnitt erzielt haben. Im Allgemeinen schnitten die Schüler der Klasse A näher am Mittelwert ab.
Beispiel 4
Der Mittelwert einer Reihe von Datenwerten ist gleich μ und seine Standardabweichung ist gleich σ. Wenn alle Datenwerte im Satz um denselben Wert k erhöht werden, wie hoch sind dann der Mittelwert und die Standardabweichung nach der Erhöhung? Lösung zu Beispiel 4
Wenn Sie alle Datenwerte auf einer Zahlengeraden darstellen und k zu diesen Werten addieren und sie erneut auf derselben Zahlengeraden grafisch darstellen, würden alle Punkte auf der Zahlengeraden um den gleichen Abstand k verschoben und daher erhöht sich auch der Mittelwert um k. Die Standardabweichung ändert sich jedoch nicht, da sie ein Maß für den Abstand zwischen den Datenwerten und dem Mittelwert ist und alle um den gleichen Wert k verschoben sind.
Der Mittelwert und die Standardabweichung der Menge { x_1, x_2 ,... x_N sind gegeben durch
\[\mu = \dfrac{\sum_{i=1}^{N} x_i}{N}\]
Und
\[\sigma =\sqrt {\dfrac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}}\]
Wir addieren nun k zu jedem Datenwert x_i und berechnen den Mittelwert und die Standardabweichung
\[\mu_k = \dfrac{\sum_{i=1}^{N} (x_i + k)}{N} = \dfrac{\sum_{i=1}^{N} x_i}{N} + \dfrac{\sum_{i=1}^{N} k}{N} = \mu + k\]
\[\sigma_k =\sqrt {\dfrac{\sum_{i=1}^{N} ((x_i + k) - \mu_A)^2}{N}} = \sqrt {\dfrac{\sum_{i =1}^{N} (x_i + k - (\mu + k))^2}{N}}\]
Vereinfachen Sie den Zähler, um ihn zu erhalten
\[\sigma_k = \sqrt {\dfrac{\sum_{i=1}^{N} (x_i - \mu )^2}{N}}\]
Wenn wir also alle Datenwerte in einer Menge um den gleichen Betrag k erhöhen, erhöht sich der Mittelwert um k, aber die Standardabweichung ändert sich nicht.
