Graph Sine and Cosine Functions

Graphs of the sine and the cosine functions of the form \[ \Large \mathbf { \color{red}{ y = a \sin(b x + c) + d}} \] and \[ \Large \mathbf { \color{red}{ y = a \cos(b x + c) + d}} \] are discussed with several examples including detailed solutions.

We start with the graph of the basic sine function $ y = \sin(x) $ and the basic cosine function $ g(x) = \cos(x) $, we then present examples of how to graph transformed versions of these same functions. An effective way of using this tutorial is to start it from the beginning and go through the examples in order.

Graph of the basic sine function: $ y = \sin(x) $

Example 1

Find the range and the period of the function $ y = \sin(x) $ and graph it.

Solution to Example 1

A unit circle (with radius 1) centered at the origin of the system of rectangular axes has 4 special points corresponding to 5 quadrantal angles $ (0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi ) $ as shown in figure 1 below. The $ x $ and $ y $ coordinates of a point on the unit circle are the cosine and the sine respectively of the corresponding angle.

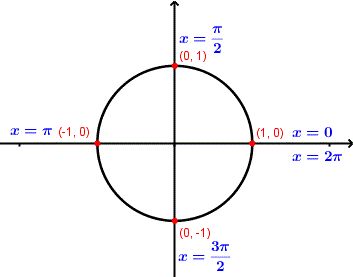
unit circle in trigonometry — Figure 1.Unit Circle in Trigonometry

$ x $ being the angle in standard position , from the unit circle we can conclude the following:

The range of $ \sin(x) $ (the y coordinates) is the set of all values in the interval \[ [-1 , 1] \; \text{or in inequality form} \; -1 \leq \sin(x) \leq 1 \]

One cycle of $ \sin(x) $ may start at $ x = 0 $ and finish at $ x = 2\pi $ after which rotation the value of $ \sin(x) $ are repeated as shown in the unit circle, we therefore say that $ \sin(x) $ has a period equal to $ 2\pi $. We need values of $ \sin(x) $ for different values of $ x $ in order to graph it. We shall use the y coordinate ( which gives $ \sin(x) $ ) of the same 5 quadrantal angles corresponding to the variable $ x (0 ,\dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, 2\pi) $ of which 3 values $ (0 , \pi , 2 \pi) $ are zeros of $ \sin(x) $, one value $ (\dfrac{\pi}{2}) $ gives a maximum value to $ \sin(x) $ and one value $ ( \dfrac{3\pi}{2} ) $ gives a minimum value to $ \sin(x) $ as shown in the table below. \[ \begin{array}{|c|c|c|} \hline x & y = \sin(x) \\ \hline 0 & 0 \\ \dfrac{\pi}{2} & 1\\ \pi & 0 \\ 3\dfrac{\pi}{2} & -1 \\ 2 \pi & 0 \\ \hline \end{array} \] The graph of $ y = \sin(x) $ is shown below over one period from $ 0 $ to $ 2\pi $ (solid line) and other periods (broken line).

graph of y = sin(x) — Figure 2. Graph of $ y = \sin(x) $

Graph of the basic sine function: $ f(x) = \cos(x) $

Example 2

Find the range and the period of the function $ y = cos(x) $ and graph it.

Solution to Example 2

We will use the same 4 special points corresponding to 5 quadrantal angles $ 0 , \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2} \text{ and } 2\pi $ as shown in the unit circle (figure 1 above). $ \cos(x) $ is given by the x coordinate of a point on the unit circle corresponding to angle $ x $ in standard position.

From the unit circle we can conclude the following:

The range of $ \cos(x) $ is the set of all values in the interval $[-1 , 1]$ in inequality form: \[ -1 \leq \cos(x) \leq 1 \]

One cycle of $ \cos(x) $ may start at $ x = 0 $ and finish at $ x = 2\pi $, after which rotation the value of $ \cos(x) $ is repeated periodically as shown in the unit circle. We therefore conclude that $ \cos(x) $ has a period equal to $ 2\pi $.

We use the values of $ \cos(x) $ for different values of $ x $ from the unit circle (see figure 1). We shall use the x coordinate (which gives $ \cos(x) $) of the same 5 quadrantal angles corresponding to the variable $ x $: $ 0 , \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}, \text{ and } 2\pi $. Of these, two values ($ 0 , 2\pi $) give the maximum value $ 1 $ of $ \cos(x) $, two values $ \dfrac{\pi}{2} $ and $ \dfrac{3\pi}{2} $ give zeros of $ \cos(x) $, and one value $ \pi $ gives a minimum value to $ \cos(x) $, as shown in the table below.

\[ \begin{array}{|c|c|c|} \hline x & y = \cos(x) \\ \hline 0 & 1 \\ \dfrac{\pi}{2} & 0 \\ \pi & -1 \\ 3\dfrac{\pi}{2} & 0 \\ 2 \pi & 1 \\ \hline \end{array} \] The graph of $ \cos(x) $ is shown below over one period from $ 0 $ to $ 2\pi $ (solid line) and more periods (broken line).

graph of y = cos(x) — Figure 3. Graph of $ y =\cos(x) $

Graph of the function: $ y = 3\sin(x) $

Example 3

Find the range and the period of the function $ y = 3\sin(x) $ and graph it.

Solution to Example 3

Comparing the given function $ y = 3 \sin(x) $ and the basic sine function $ y = \sin(x) $, there is a multiplication factor of 3. There is no horizontal stretching or shifting since the variable $ x $ appears in the same "way" in both functions. \[ \text{Period} = 2\pi \] We have already made a table for $ \sin(x) $ above; let us extend it and include the given function $ y = 3 \sin(x) $ to graph. Note: To obtain values for the function $ 3 \sin(x) $, you multiply the values of the function $ \sin(x) $ by 3 as shown in the table below. From the table: \[ \text{Range: } -3 \leq 3 \sin(x) \leq 3 \] \[ \begin{array}{|c|c|c|} \hline x & \sin(x) & y = 3 \sin(x) \\ \hline 0 & 0 & 0 \\ \dfrac{\pi}{2} & 1 & 3 \\ \pi & 0 & 0 \\ 3\dfrac{\pi}{2} & -1 & -3 \\ 2 \pi & 0 & 0 \\ \hline \end{array} \] The graph of $ 3 \sin(x) $ is shown below over one period from 0 to 2π and as expected there is a vertical stretching of a factor of 3 (compare to $ y = \sin(x) , red) $. The period did not change as expected but the range is now: $ [-3 , 3] $ or in inequality form : $ -3 \leq 3 \sin(x) \leq 3 $

graph of y = 3sin(x) — Figure 4. Graph of $ y = 3 \sin(x) $

Graph of the function: $ y = - 2 \cos(x) $

Example 4

Find the range and the period of the function $ y = -2 \cos(x) $ and graph it.

Solution to Example 4

Comparing the given function $ y = - 2 cos(x) $ and the basic cosine function $ y = cos(x) $, there is a vertical stretching of a factor of 2 and there is also a reflection on the x axis because of the minus in - 2. There is no horizontal stretching or shifting since the variable x appear in the same "way" in both functions.

Period = 2π

A table for $ \cos(x) $ was already made above, let us extend it to include the given function $ y = - 2 \cos(x) $ to graph.

From table; range: $ -2 \leq -2 \cos(x) \leq 2 $

In general the range of functions of the form $ y = a \sin(x) $ or $ y = a \cos(x) $ is given by the interval \[ [ - |a| , |a| ] \; \text{or in inequality form} - |a| \le y \le |a| \] \[ \begin{array}{|c|c|c|} \hline x & \cos(x) & y = -2 \cos(x) \\ \hline 0 & 1&-2 \\ \dfrac{\pi}{2} & 0 & 0 \\ \pi & -1& 2 \\ 3\dfrac{\pi}{2} & 0 & 0 \\ 2 \pi & 1 &-2 \\ \hline \end{array} \]

The graph of $ -2 \cos(x) $ is shown below over one period from $ 0 $ to $ 2\pi $ (blue solid line) compared to $ y = \cos(x) $ (red) and we can see that there is a stretching of factor 2 and reflection.

graph of y = - 2 cos(x) — Figure 5. Graph of $ y = -2 \cos(x) $

Graph of the function: $ y = \sin(2 x) $

Example 5

Find the period of the function $ y =\sin(2 x) $ and graph it.

Solution to Example 5

Comparing the given function $ y = \sin(2 x) $ and the basic sine function $ y = \sin(x) $, there is a horizontal shrinking of a factor of $ 2 $ because of the $ 2x $ in $ \sin(2 x) $.

Explanation For the function $ y =\sin(2 x) $ to go through one period, $ 2 x $ will have to be as follows \[0 \leq 2x \leq 2\pi \] divide by $ 2 $ all terms of the above inequality, we obtain \[ 0 \leq x \leq \pi \] this is the interval over one period to be used to graph $ y =\sin(2 x) $ Hence the period of $ \sin(2x) $ is gibven by \[ \pi - 0 = \pi \]

In general the period of functions of the form $ y = \sin( b x) $ or $ y = \cos( b x) $ is given by \[ \dfrac{\ 2\pi}{|b|} \] the period is always positive. A table for $ \sin(2 x) $ is made in a similar way as a $ y = \sin(x) $ with one difference in the values of $ x $ over one period from $ 0 to \pi $ (one period).

The values of $ x = 0, \pi , \pi/4 , \pi/2 , 3\pi/4 $ split the period into 4 equal intervals. \[ \begin{array}{|c|c|c|} \hline x & y = \sin(2 x) \\ \hline 0 & 1\\ \dfrac{\pi}{4} & 1 \\ \dfrac{\pi}{2} & 0 \\ 3\dfrac{\pi}{4} & -1\\ \pi & 0\\ \hline \end{array} \] The graph of $ y = \sin(2 x) $ is shown below over one period from $ 0 $ to $ \pi $ (blue solid line) compared to $ y =\sin(x) $ which has a period of $ 2\pi $ (red).

graph of y =\sin(2x) — Figure 6. Graph of $ y = \sin(2x) $

Graph of the function: $ y = \cos(2 x - \dfrac{\pi}{4}) $

Example 6

Find the period, phase shift of the function $ y = \cos\left(2x - \dfrac{\pi}{4}\right) $ and graph it.

Solution to Example 6

Rewrite the given function as \[ y = \cos\left(2(x - \dfrac{\pi}{8})\right) \] We first start by ignoring the term $ -\dfrac{\pi}{8} $ and define a period for $ y = \cos(2x) $ \[ 0 \leq 2x \leq 2\pi \] Divide all terms by 2 to obtain \[ 0 \leq x \leq \pi \] period is $ \pi $ as already calculated above.

For the function $ y = \cos\left(2(x - \dfrac{\pi}{8})\right) $ to go through one period the expression $ 2(x - \dfrac{\pi}{8}) $ will have to be as follows: \[ 0 \leq 2(x - \dfrac{\pi}{8}) \leq 2\pi \] Divide all terms by 2 \[ 0 \leq x - \dfrac{\pi}{8} \leq \pi \] Add $ \dfrac{\pi}{8} $ to all terms \[ \dfrac{\pi}{8} \leq x \leq \pi + \dfrac{\pi}{8} \] This is the interval over one period to be used to graph $ y = \cos\left(2x - \dfrac{\pi}{4}\right) $

When we compare the interval of one period for $ \cos(2x) $ which is \[ 0 \leq x \leq \pi \] and the interval for one period of $ \cos\left(2(x - \dfrac{\pi}{8})\right) $ which is \[ \dfrac{\pi}{8} \leq x \leq \pi + \dfrac{\pi}{8} \] the only difference is the phase shift to the right by $ \dfrac{\pi}{8} $

In general the phase shift of functions of the form $ y = \sin(bx + c) $ or $ y = \cos(bx + c) $ is given by \[ -\dfrac{c}{b} \] If the phase shift is positive the shift is to the right, and if it is negative, the shift is to the left.

We construct the table of values as follows:

We have seen above that in this example one period starts from x = π/8 and finishes at x = π + π/8 = 9π/8. Hence we start the table using these two points.

We have seen above that in this example one period starts from $ x = \dfrac{\pi}{8} $ and finishes at $ x = \pi + \dfrac{\pi}{8} = \dfrac{9\pi}{8}$ Hence we start the table using these two points.

One Period

We next find the mid value between $ x = \pi/8 $ and $ x = 9\pi/8 $, calculated as follows: \[ \dfrac{1}{2} \left( \dfrac{\pi}{8} + \dfrac{9\pi}{8} \right) = \dfrac{5\pi}{8} \] and put it in the table.

Three Points in One Period

We next find the mid value between x = π/8 and 5 π/8 calculated as follows: (1/2)(π/8 + 5π/8) = 3 π/8 ; and the mid value between 5 π/8 and 9π/8 calculated as follows (1/2)(5π/8 + 9π/8) = 7 π/8 and put all these in the table as follows We next find the mid value between $ x = \dfrac{\pi}{8} $ and $ \dfrac{5\pi}{8} $ calculated as follows: \[ \dfrac{1}{2} \left( \dfrac{\pi}{8} + \dfrac{5\pi}{8} \right) = \dfrac{3\pi}{8} \] and the mid value between $\dfrac{5\pi}{8}$ and $\dfrac{9\pi}{8}$ calculated as follows \[ \dfrac{1}{2} \left( \dfrac{5\pi}{8} + \dfrac{9\pi}{8} \right) = \dfrac{7\pi}{8} \] and put all these in the table as follows

Five Points in One Period We have split the one period interval into 4 equal intervals and these make it easy to evaluate the given function $ y =\sin(2x) $ which will have the same maximum, minimum values at similar position but within the interval $ \dfrac{\pi}{8} , \dfrac{9\pi}{8} $. We now complete the table by putting the values of the function.

Values of y = cos(2 x - pi/4) The graph of $ y = \cos(2 x - \dfrac{\pi}{4}) $ (blue) is compared to the graph of $\cos(2 x) $ (red). They are similar except for the shift of $ \dfrac{\pi}{8} $ the right.

graph of y = cos(2x - pi/4) — Figure 7. Graph of $ y = \cos(2 x - \dfrac{\pi}{4}) $

Graph of the function: $ y =\sin(3 x + \dfrac{\pi}{3}) $

Example 7

Find the period and phase shift of the function $ y =\sin(3 x + \dfrac{\pi}{3}) $ and graph it.

Solution to Example 7

The period is given by: \[ \dfrac{2\pi}{|b|} = \dfrac{2\pi}{3} \]

The phase shift is calculated as follows \[ \dfrac{-c}{b} = \dfrac{-\pi/3}{3} = \dfrac{-\pi}{9} \] We expect the graph of $ y = \sin(3x + \dfrac{\pi}{3}) $ to be the graph of $ y = \sin(3x) $ shifted by $ \dfrac{\pi}{9} $ to the left because of the minus sign in the phase shift.

For the function $ y = \sin(3x + \dfrac{\pi}{3}) $ to go through one period the expression $ 3x + \dfrac{\pi}{3} $ will have to be as follows \[ 0 \leq 3x + \dfrac{\pi}{3} \leq 2\pi \] Solve the above inequality for $ x $ to obtain the interval corresponding to one period. \[ -\dfrac{\pi}{9} \leq x \leq \dfrac{5\pi}{9} \] Find the mid values as was done in example 6 and complete the table of values.

$Values of y =\sin(3 x + pi/3)$ The graph of the given function $ y =\sin(3 x + \dfrac{\pi}{3}) $ (blue) is compared to the graph of $\sin(3 x) $ (red). They are similar except for the shift of $ \dfrac{\pi}{9} $ to the left.

graph of y = sin(3x + pi/3) — Figure 8. Graph of $ y = \sin(3x + \dfrac{\pi}{3} $

Graph of the function: $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $

Example 8

Find the range, period and phase shift of the function $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $ and graph it.

Solution to Example 8

We know that the range of $ \sin(2x - \pi/5) $ is given by the interval $[-1 , 1]$ or as an inequality we write \[ -1 \leq \sin(2x - \pi/5) \leq 1 \] Multiply all terms of the inequality by $-2$ and change the symbols of inequality \[ 2 \geq -2\sin(2x - \pi/5) \geq -2 \] Add $+1$ to all terms of the inequality and rewrite as \[ -2 + 1 \leq -2\sin(2x - \pi/5) + 1 \leq 2 + 1 \] Which gives the range of the given function as \[ -1 \leq -2\sin(2x - \pi/5) + 3 \leq 3 \] In general the range of the function $ y = a\sin(bx + c) + d $ or $ y = a\cos(bx + c) + d $ is given by the interval \[ [ -|a| + d , |a| + d ] \quad \text{or in inequality form} \quad -|a| + d \leq y \leq |a| + d \] The period is given by \[ \dfrac{2\pi}{|b|} = \dfrac{2\pi}{|2|} = \pi \] The phase shift is given by \[ -\dfrac{c}{b} = -\dfrac{-\pi/5}{2} = \dfrac{\pi}{10} \] To graph $ y = -2\sin(2x - \pi/5) + 1 $ over one period the expression $ 2x - \pi/5 $ has to go through one period as follows \[ 0 \leq 2x - \pi/5 \leq 2\pi \] Solve the above inequality to obtain \[ \dfrac{\pi}{10} \leq x \leq \dfrac{11\pi}{10} \] Use the lowest value $ \dfrac{\pi}{10} $ and the highest value $ \dfrac{11\pi}{10} $ in the above inequality (which gives a period) to construct a table of values by splitting the period into 4 equal intervals as follows

$Values of y = - 2 sin(2 x - \dfrac{\pi}{5}) + 1$ It is important to note that the graph over one period is inscribed inside a rectangle of length from $ \dfrac{\pi}{10} $ to $ 11\dfrac{\pi}{10} $ which the interval over one period found above by solving the inequality $ 0 \leq (2x - \pi/5) \leq 2\pi $ and a width from the minimum and the maximum (range) values of $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $ equal to $ -2 + 1 = - 1 $ and $ 2 + 1 = 3 $ which is the range already found in the table.

graph of y = -2 sin(2x - π/5) + 1 — Figure 9. Graph of $ y = - 2\sin(2 x - \dfrac{\pi}{5}) + 1 $

Exercise

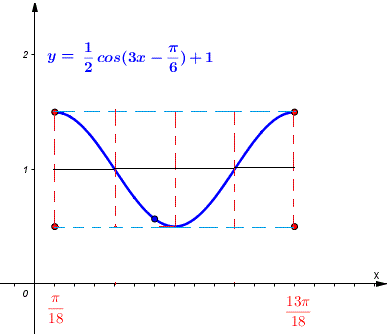
For the function given below, find the starting and finishing x values over one period, the range and Graph it over one period. \[ y = \dfrac{1}{2} \cos\left(3x - \dfrac{\pi}{6}\right) + 1 \]

Solutions to Above Exerciss

one period : $ \dfrac{\pi}{18} \leq x \leq \dfrac{13\pi}{18} $ , range : $ [1/2 , 3/2] $ . See graph below

graph of y = (1/2) cos(3x - π6) + 1 — Figure 11. graph of $ y = \dfrac{1}{2} \cos\left(3x - \dfrac{\pi}{6}\right) + 1 $

Graph Sine and Cosine Functions

Graph of the basic sine function: \( y = \sin(x) \)

Example 1

Solution to Example 1

Graph of the basic sine function: \( f(x) = \cos(x) \)

Example 2

Solution to Example 2

Graph of the function: \( y = 3\sin(x) \)