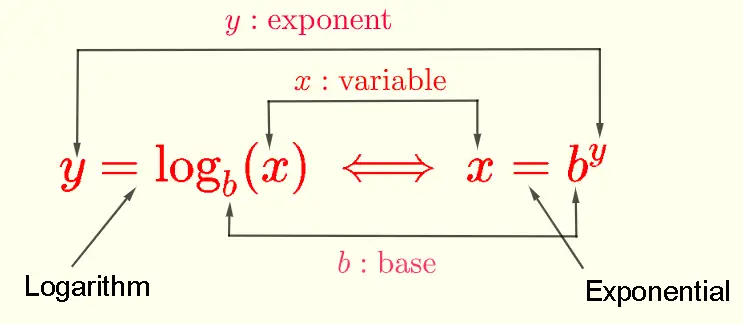
 where the symbol \( \iff \) means "is equivalent to", \( y \) is the exponent, \( b \) is the base such that \( b \gt 0 , b \ne 1 \) and \( x \gt 0 \)
where the symbol \( \iff \) means "is equivalent to", \( y \) is the exponent, \( b \) is the base such that \( b \gt 0 , b \ne 1 \) and \( x \gt 0 \)
Questions on Logarithm and exponential with answers and detailed solutions, for grade 11, are presented.
Page Content
1) One of the most important property of logarithmic and exponential functions is that they are inverse of each other and therefore we can convert exponential and logarithmic expressions using the following:
 where the symbol \( \iff \) means "is equivalent to", \( y \) is the exponent, \( b \) is the base such that \( b \gt 0 , b \ne 1 \) and \( x \gt 0 \)
where the symbol \( \iff \) means "is equivalent to", \( y \) is the exponent, \( b \) is the base such that \( b \gt 0 , b \ne 1 \) and \( x \gt 0 \)
Numerical example \[ 2 = \log_3 (9) \iff 9 = 3^2 \] 2) One-to-one properties of logarithmic and exponential functions
a) If \( \quad b^x = b^y \quad \), then \( \quad x = y \)
b) If \( \quad \log_b (x) = \log_b (y) \quad \), then \( \quad x = y \) , (NOTE: the logs on both sides have the same base)
a) \( \log_x (a) = c \) as an exponential \( a = x^c \)
b) \( \log_b (2x + 1) = 3 \) as an exponential \( 2x + 1 = b^3 \)
a) \( 3^x = m \) as a logarithm \( x = \log_3 (m) \)
b) \( x^2 = a \) as a logarithm \( 2 = \log_x (a) \)
a)
let \[ y = \log_2 16 \]
convert to exponential form: \[ 2^y = 16 \]
Use the fact that \( 16 = 2^4\) to write \[ 2^y = 2^4 \]
hence using the one to one property of the exponential given above, " If \( 2^y = 2^4 \), then y = 4" , we write:
\[ y = \log_2 16 = 4 \]
b)
let \[ y = \log_3 27 \]
convert to exponential form: \[ 3^y = 27 \]
Use the fact that \( 27 = 3^3 \) to write \[ 3^y = 3^3 \]
hence using the one to one property 2 b) gives then \[ y = 3 \]
hence : \[ y = \log_3 27 = 3 \]
c)
let \[ y = \log_2 (1/32) \]
convert to exponential form: \[ 2^y = \dfrac{1}{32} \]
Use the fact that \( \dfrac{1}{32} = \dfrac{1}{2^5} = 2^{-5} \) to write \[ 2^y = 2^{-5} \]
and the one to one property of the exponential function gives: \[ y = -5 \]
hence \[ y = \log_2 (1/32) = -5 \]
d)
let \[ y = \log_{25} 5 \]
convert to exponential form: \[ 25^y = 5 \]
Use the fact that \( 5 = \sqrt{25} = 25^{1/2} \) to write \[ 25^y = 25^{1/2} \]
hence \[ y = \log_{25} 5 = 1/2 \]
e)
Let \( y = \log \sqrt{10} \) ( note log base 10 ); convert to exponential form: \[ 10^y = \sqrt{10} = 10^{1/2} \]
hence \[ y = \log \sqrt{10} = 1/2 \]
f)
Let \( y = \log_b 1 \) ; convert to exponential form: \[ b^y = 1 = b^0 \quad \text{hence} \quad y = \log_b 1 = 0 \]
g)
let \( y = \log_{0.1} 10 \) convert to exponential form \[ 0.1^y = 10 \]
Use \( 10 = 1 / 0.1 = 0.1^{-1} \) , hence \[ 0.1^y = 0.1^{-1} \quad \text{ which gives} \quad y = \log_{0.1} 10 = - 1 \]
a)
\( \log_2 x = 3 \) ; convert to exponential form: \[ x = 2^3 = 8 \]
b)
\( \log_x 8 = 3 \) ; convert to exponential form: \[ 8 = x^3 \] write 8 as \[ 8 = 2^3 = x^3\] hence \[ x = 2 \]
c)
\( \log_3 x = 1 \) ; convert to exponential form: \[ x = 3^1 = 3 \]
d)
\( \log_{5.6} x = 0 \) ; convert to exponential form: \[ x = 5.6^0 = 1 \]
e)
\( \log_2 (3x + 1) = 4 \) ; convert to exponential form: \[ 3x + 1 = 2^4 = 16 \] solve for x: \[ 3x + 1 = 16 , 3x = 15 , x = 5 \]
f)
\( \log_3 \dfrac{1}{x+1} = 2 \) ; convert to exponential form: \[ \dfrac{1}{x+1} = 3^2 = 9 \] solve for x: \[ 1 = 9 (x + 1) , x = - 8 / 9 \]
g)
\( \log_4 \dfrac{x+1}{2x-1} = 0 \) ; convert to exponential form: \[ \dfrac{x+1}{2x-1} = 4^0 = 1 \] solve for x: \[ x + 1 = 2x - 1 , x = 2 \]
h)
\( \log ( 1/x + 1 ) = 2 \) ; convert to exponential form: \[ 1/x + 1 = 10^2 = 100 \] solve for x: \[ 1/x + 1 = 100 , 1/x = 99 , x = 1/99 \]
i)
\( \log_x 0.0001 = 4 \) ; convert to exponential form: \[ x^4 = 0.0001 = 1/10000 = 1/10^4 = (1/10)^4 \]
which gives \[ x^4 = (1/10)^4 \]
hence \[ x = 1/10 \].
Note that in the above equation, the bases of the two exponential are both equal to \( b \).
a)
\( 3^x = 9 = 3^2 \) hence \[ x = 2 \]
b)
\( 4^{2x + 1} = 16 = 4^2 \), which gives \[ 4^{2x + 1} = 4^2 \] hence \[ 2x + 1 = 2 , x = 1 / 2 \]
c)
\( \left(\dfrac{1}{2} \right)^x = 2 \)
write \( 2 \) as \ 2 = \left(\dfrac{1}{2} \right)^{-1} \]
which gives \[ \left(\dfrac{1}{2} \right)^x = \left(\dfrac{1}{2} \right)^{-1} \]
hence \[ x = - 1 \]
d)
\( 10^x = 5 \) , convert the exponential to logarithm base 10: \[ \quad x = \log_{10} 5 \]
e)
\( \left(\dfrac{1}{3} \right)^{x/2 - 2} = 9 = 3^2 \).
Write \( 3^2 \) as \[ \left(\dfrac{1}{3} \right)^{-2} \]
which gives \[ \left(\dfrac{1}{3} \right)^{x/2 - 2} = \left(\dfrac{1}{3} \right)^{-2} \].
Hence \[ x/2 - 2 = - 2 \]
solve to obtain \[ x = 0 \]
f)
\( 0.01^x = 100 \). Write :
\[ 100 = \dfrac{1}{0.01} = 0.01^{-1} \quad \text{which gives} \quad 0.01^x = 0.01^{-1} \]
hence \[ x = -1 \]
g)
Given the equation: \[ 2^{2x} - 6 \cdot 2^x = - 8 \]
Note that \[ 2^{2x} = (2^x)^2 \]
Let \( u = 2^x \) and write \[ u^2 = (2^x)^2 = 2^{2x} \]
We now substitute \( 2^x \) by \( u \) and \( 2^{2x} \) by \( u^2 \) in the given equation and rewrite the equation in terms of \( u \) only and in standard form as follows
\[ u^2 - 6 u + 8 = 0 \]
Solve the above quadratic equation by factoring:
\[ (u - 2)(u - 4) = 0 \]
solutions in u: \[ u = 2 \quad \text{and} \quad u = 4 \]
We now solve for \( x \) using the substitution made above:
\[ u = 2 = 2^x \quad \text{gives the solution:} \quad x = 1 \]
\[ u = 4 = 2^x = 2^2 \quad \text{gives the solution:} \quad x = 2 \]