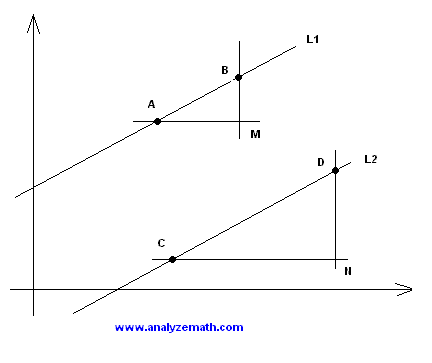
Hence, \[ \frac{BM}{DN} = \frac{MA}{NC} \]
\[ \frac{BM}{MA} = \frac{DN}{NC} \]
This page presents a clear geometric proof showing that the slopes of two parallel lines are equal. It also includes several worked examples and practice questions with detailed solutions.

Hence, \[ \frac{BM}{DN} = \frac{MA}{NC} \]
\[ \frac{BM}{MA} = \frac{DN}{NC} \]
Which of the following lines are parallel?
\[ \begin{aligned} \text{a)}\ & y = 2x - 3 \\ \text{b)}\ & 2x - y = 2 \\ \text{c)}\ & -4y + 2x = 0 \\ \text{d)}\ & -4y + 8x = 9 \end{aligned} \]
Solution
Write each equation in slope–intercept form \(y = mx + b\).
\[ \begin{aligned} \text{a)}\ & y = 2x - 3 \Rightarrow m = 2 \\ \text{b)}\ & y = 2x - 2 \Rightarrow m = 2 \\ \text{c)}\ & y = \tfrac{1}{2}x \Rightarrow m = \tfrac{1}{2} \\ \text{d)}\ & y = 2x - \tfrac{9}{4} \Rightarrow m = 2 \end{aligned} \]
The lines in parts (a), (b), and (d) have equal slopes and are therefore parallel.
Find \(k\) so that the lines \[ 6kx - 3y = 9 \quad \text{and} \quad -4x + 5y = 7 \] are parallel.
Solution
\[ \begin{aligned} 6kx - 3y &= 9 \Rightarrow y = 2kx - 3 \Rightarrow m_1 = 2k \\ -4x + 5y &= 7 \Rightarrow y = \tfrac{4}{5}x + \tfrac{7}{5} \Rightarrow m_2 = \tfrac{4}{5} \end{aligned} \]
Parallel lines have equal slopes: \[ 2k = \tfrac{4}{5} \]
\[ k = \tfrac{2}{5} \]
Find \(a\) so that the line through \((1,2)\) and \((0,3)\) is parallel to the line through \((a,2)\) and \((-2,7)\).
Solution
\[ m_1 = \frac{3 - 2}{0 - 1} = -1 \]
\[ m_2 = \frac{7 - 2}{-2 - a} = \frac{5}{-2 - a} \]
Set the slopes equal: \[ \frac{5}{-2 - a} = -1 \]
\[ a = 3 \]
Find the coordinates of point \(D (a,b) \) so that \(A(0,2)\), \(B(2,6)\), \(C(8,8)\), and \(D\) form a parallelogram.

Solution
\[ m_{AB} = \frac{6 - 2}{2 - 0} = 2 \]
\[ m_{DC} = \frac{8 - b}{8 - a} \Rightarrow 2 = \frac{8 - b}{8 - a} \Rightarrow 8 - b = 16 - 2a \]
\[ m_{BC} = \frac{8 - 6}{8 - 2} = \tfrac{1}{3}, \quad m_{AD} = \frac{b - 2}{a} \Rightarrow \tfrac{1}{3} = \frac{b - 2}{a} \Rightarrow a = 3b - 6 \]
Solving the system gives: \[ b = 4, \quad a = 6 \]
\[ D(6,4) \]
Find the equation of a line through \((2,1)\) parallel to the line through \((-1,2)\) and \((3,4)\).
Solution
\[ m = \frac{4 - 2}{3 - (-1)} = \tfrac{1}{2} \]
\[ y - 1 = \tfrac{1}{2}(x - 2) \Rightarrow y = \tfrac{1}{2}x \]
Find the equation of a line through \((-1,1)\) parallel to \[ 2y + 4x = 2 \]
Solution
\[ y = -2x + 1 \Rightarrow m = -2 \]
\[ y - 1 = -2(x + 1) \Rightarrow y = -2x - 1 \]
Equations of Lines in Different Forms
Tutorial on Equation of a Line
Line Geometry Problems
Lines Through Two Points (Parallel & Perpendicular)