Grade 8 Problems on Circles and Solutions

The diameter of circle \( C_1 \) is equal to 20 units, so its radius is 10 units. The area \( A \) of the largest circle \( C_1 \) is: \[ A = \pi (10)^2 \] The diameter of circle \( C_2 \) is equal to the radius of circle \( C_1 \), which is 10 units. The diameter of circle \( C_3 \) is equal to the radius of circle \( C_2 \), which is 5 units. Therefore, the radius of circle \( C_3 \) is 2.5 units. We now calculate the area \( B \) of the smallest circle \( C_3 \): \[ B = \pi (2.5)^2 \] The ratio of \( A \) to \( B \) is given by: \[ \dfrac{A}{B} = \dfrac{\pi (10)^2}{\pi (2.5)^2} \] Simplifying: \[ = \dfrac{(10)^2}{(2.5)^2} = \left(\dfrac{10}{2.5}\right)^2 = 4^2 = 16 \]

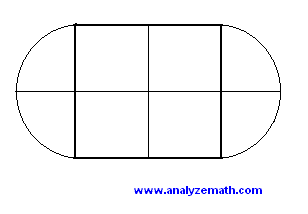
The garden is made up of 4 squares and 2 semicircles. The total area of the 4 squares is: \[ 4 \times 4 = 16 \text{ square meters} \] Since the area of one small square is 4 square meters, the side length \( s \) of each square is related to its area by: \[ s^2 = 4 \] Hence \[ s = \sqrt{4} = 2 \text{ meters} \] The radius of each semicircle is equal to the side of the square, so the radius is \( 2 \) meters. The two semicircles together form a complete circle. The area of the circle is: \[ \pi \times 2^2 = 4\pi \] So, the total area of the garden is: \[ 16 + 4\pi \approx 16 + 12.56 = 28.56 \text{ square meters} \quad (\text{using } \pi \approx 3.14) \]

One full rotation of the sprinkler would irrigate an area enclosed by a circle of radius 12 m. Hence, the area of the garden that the sprinkler can irrigate is given by the formula: \[ A = \pi r^2 = \pi (12)^2 = 144\pi \approx 452 \text{ square meters} \]

The walkway is enclosed between a smaller circle of radius \( 10 \) meters and a larger circle of radius \( 10+1 = 11 \) meters. Therefore, the area of the walkway is equal to the area enclosed by the larger circle minus the area enclosed by the smaller circle. \[ \text{Area of walkway} = \pi \times 11^2 - \pi \times 10^2 = 121\pi - 100\pi = 21\pi \text{ square meters.} \]

The \$19.99 is the total cost of the whole pizza, whose area is: \[ \pi \times \left(\dfrac{36}{2}\right)^2 = 1017.87 \, \text{square cm} \] The cost of 1 square cm is equal to: \[ \dfrac{19.99}{1017.87} \approx 0.02 \, \text{dollars} = 2 \, \text{cents per square cm} \]

The fencing will be put around the circular garden, and therefore the length of the fencing is equal to its circumference of the garden. The radius \( r \) of the garden is found using the area formula: \[ \pi \times r^2 = 5 \] Solving for \( r^2 \): \[ r^2 = \dfrac{5}{\pi} \] Taking the square root of both sides: \[ r = \sqrt{\dfrac{5}{\pi}} \approx 1.26 \text{ meters} \] The circumference of the garden is: \[ 2r \times \pi = 2 \times 1.26 \times \pi \approx 8 \text{ meters} \quad (\text{rounded to the nearest meter}) \] The length of the fencing needed is 8 meters.

If \( r \) is the radius of the disk, its area (before the increase) is given by: \[ A_{\text{before}} = \pi r^2 \] If the radius is increased by 20%, the new radius becomes: \[ r_{\text{new}} = r + 20\% \, r = r + \dfrac{20}{100} r = 1.2 r \] The area (after the increase) of the disk becomes: \[ A_{\text{after}} = \pi (1.2r)^2 = 1.44 \pi r^2 \] The change in area is: \[ \text{Change in area} = A_{\text{after}} - A_{\text{before}} = 1.44 \pi r^2 - \pi r^2 \] \[ = \pi r^2 (1.44 - 1) = 0.44 \pi r^2 \] The percent change in area is: \[ \text{Percent change in area} = \left( \dfrac{\text{Change}}{A_{\text{before}}} \right) \times 100\% = \left( \dfrac{0.44 \pi r^2}{\pi r^2} \right) \times 100\% \] \[ = 0.44 \times 100\% = 44\% \]

If the table has a diameter of 100 inches and the tablecloth hangs 15 inches around the table, then the diameter of the tablecloth is equal to: \[ 100 + 15 + 15 = 130 \text{ inches} \] and its radius \( r \) is: \[ r = \dfrac{130}{2} = 65\] The area of the tablecloth is equal to: \[ A = \pi r^2 = \pi \left( 65 \right)^2 \] \[ = 4225 \pi \approx 13,267 \text{ square inches} \]

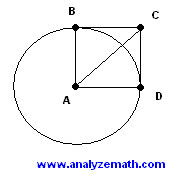\[ \text{Area of the circle} = \pi r^2 = 100 \] Solving for \( r^2 \): \[ r^2 = \dfrac{100}{\pi} \] Next, we use the Pythagorean theorem in triangle \( ABC \) to find the length of \( AC \): \[ AC^2 = AB^2 + BC^2 \] Since both \( AB \) and \( BC \) are equal to \( r \), we have: \[ AC^2 = r^2 + r^2 = 2r^2 \] Substituting the value of \( r^2 \): \[ AC^2 = 2 r^2 = 2 \left( \dfrac{100}{\pi} \right) = \dfrac{200}{\pi} \] Finally, taking the square root: \[ AC = \sqrt{\dfrac{200}{\pi}} = 10 \sqrt{\dfrac{2}{\pi}} \approx 8 \text{ cm} \]

Let \(R_A\) be the radius of circle \(A\) and \(R_B\) be the radius of circle \(B\). The perimeters \(P_A \) and \( P_B \) of circles \( A \) and \( B\) are given by: \[ P_A = 2 \pi R_A \quad \text{and} \quad P_B = 2 \pi R_B \] The ratio of the perimeters of circle \(A\) to the perimeter of circle \(B\) gives: \[ \dfrac{P_A}{P_B} = \dfrac{2 \pi R_A}{ 2 \pi R_B} = \dfrac{3}{1} = \dfrac{R_A}{R_B} \] which simplifies to: \[ R_A = 3 R_B \] Now, we express the areas \(A_A\) and \(A_B\) of the two circles: \[ A_A = \pi R_A^2 = \pi (3 R_B)^2 \] \[ A_B = \pi R_B^2 \] The ratio of the areas is given by: \[ \dfrac{A_A}{A_B} = \dfrac{\pi (3 R_B)^2}{\pi R_B^2} \] \[ = \dfrac{\pi 9 R_B^2}{\pi R_B^2} \] \[ = 9 \] Thus, the ratio of the areas is \(9:1\).

Let \( O \) be the center of the circle.

Let \( P \) be the point where the perpendicular from the center \( O \) meets the chord \( AB \), and let \( AB \) be the chord we need to find.

\( OP = 6 \) units (distance from center to chord).

By the Intersecting Chord Theorem, the perpendicular bisects the chord, so we have two right triangles: \( \triangle OAP \) and \( \triangle OBP \), both of which are congruent.

\( OA = OB = 10 \) units (radius of the circle).

Here is the diagarm for the problem.

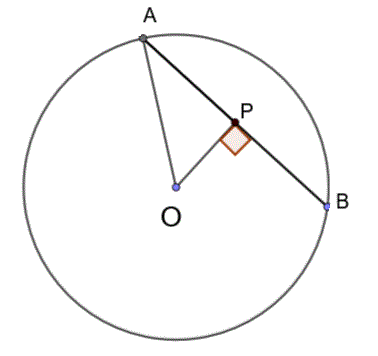
Using the Pythagorean Theorem in \( \triangle OAP \): \[ OA^2 = OP^2 + AP^2 \] Substituting the known values: \[ 10^2 = 6^2 + AP^2 \] \[ 100 = 36 + AP^2 \] \[ AP^2 = 100 - 36 = 64 \] \[ AP = \sqrt{64} = 8 \] Since \( P \) is the midpoint of \( AB \), the length of the entire chord \( AB \) is twice the length of \( AP \): \[ AB = 2 \times AP = 2 \times 8 = 16 \] The length of the chord \( AB \) is 16 units.