The lengths of two sides of a triangle are 20 mm and 13 mm. Which of these lengths cannot represent the length of the third side?
- 35 mm
- 10 cm
- 20 mm
- 45 mm
Solution
In any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Given two sides with lengths \(20\, \text{mm}\) and \(13\, \text{mm}\), their sum is
\[ 20 + 13 = 33 \text{ mm}. \]Therefore, the third side length \(x\) must satisfy
\[ x \lt 33 \text{ mm}. \]Now check the given options:
- \(35 \text{ mm} > 33 \text{ mm}\) — not possible,
- \(10 \text{ cm} = 100 \text{ mm} > 33 \text{ mm}\) — not possible,
- \(20 \text{ mm} \lt 33 \text{ mm}\) — possible,
- \(45 \text{ mm} > 33 \text{ mm}\) — not possible.
Hence, the third side cannot be \(35\, \text{mm}\), \(10\, \text{cm}\), or \(45\, \text{mm}\).
ABC is an isosceles triangle. Find the size of angle \( \angle ABC \).
Solution
The sum of the angles in triangle \(ABC\) is
\[ 72^\circ + \angle ACB + \angle ABC = 180^\circ. \]Since \(ABC\) is isosceles, angles \(ACB\) and \(ABC\) are equal:
\[ \angle ACB = \angle ABC. \]Let \(\angle ABC = x\). Then,
\[ 72^\circ + 2x = 180^\circ \implies 2x = 180^\circ - 72^\circ = 108^\circ \implies x = 54^\circ. \]Therefore,
\[ \angle ABC = 54^\circ. \]The perimeter of an equilateral triangle is 210 cm. What is the length of one side of this triangle?
Solution
In an equilateral triangle, all sides are equal. If the length of one side is \(x\), then the perimeter is
\[ 3x = 210. \]Solving for \(x\),
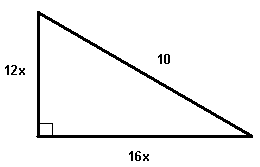
\[ x = \frac{210}{3} = 70 \text{ cm}. \]Find \(x\) so that the triangle shown below is a right triangle.
Solution
Use Pythagoras' theorem:
\[ (12x)^2 + (16x)^2 = 10^2. \]Calculate each term:
\[ 144 x^2 + 256 x^2 = 100. \]Combine like terms:
\[ 400 x^2 = 100. \]Solve for \(x^2\):
\[ x^2 = \frac{100}{400} = \frac{1}{4}. \]Taking the positive root (since length is positive):
\[ x = \frac{1}{2}. \]What will be the vertices of the triangle obtained by reflection on the x-axis of the triangle defined by the vertices \((1, 2), (2, -3)\), and \((4, -1)\)?
Solution
When a point \((x, y)\) is reflected about the x-axis, the y-coordinate changes sign, so the reflected point is \((x, -y)\).
Thus, the reflected vertices are:
\[ (1, -2), \quad (2, 3), \quad (4, 1). \]The two triangles shown below are similar. Find the length of the hypotenuse of the larger triangle.
Solution
In similar triangles, corresponding sides are proportional. Let \(h\) be the hypotenuse of the smaller triangle and \(H\) the hypotenuse of the larger triangle. Then,
\[ \frac{8}{15} = \frac{h}{H}. \]Use Pythagoras' theorem to find \(h\):
\[ h^2 = 8^2 + 6^2 = 64 + 36 = 100, \] \[ h = 10. \]Substitute \(h = 10\) in the proportion:
\[ \frac{8}{15} = \frac{10}{H}. \]Cross-multiply:
\[ 8H = 150, \] \[ H = \frac{150}{8} = 18.75. \]A 13-foot ladder is leaning against a vertical wall. The foot of the ladder is 4 feet from the wall. What is the height of the point where the ladder touches the wall? (Round your answer to the nearest tenth of a foot.)
Solution
The ladder, the wall, and the ground form a right triangle where the ladder is the hypotenuse of length 13 feet and one side is 4 feet. Let the height be \(x\). Use Pythagoras' theorem:
\[ x^2 + 4^2 = 13^2. \]Solve for \(x^2\):
\[ x^2 = 169 - 16 = 153. \]Calculate \(x\):
\[ x = \sqrt{153} \approx 12.4 \text{ feet (rounded to the nearest tenth)}. \]This height \(x\) is the point where the ladder touches the wall.
The length of the hypotenuse of a right triangle is 40 cm. One of its angles is \(45^\circ\). What are the exact lengths of the other two sides of the triangle?
Solution
In a right triangle with one angle \(45^\circ\), the other non-right angle is also \(45^\circ\). Thus, the triangle is isosceles with the two legs equal. Let each leg length be \(x\).
Using Pythagoras' theorem:
\[ x^2 + x^2 = 40^2, \] \[ 2x^2 = 1600, \] \[ x^2 = 800 = 2 \times 400, \] \[ x = \sqrt{2 \times 400} = 20 \sqrt{2}. \]Hence, the lengths of the other two sides are each \(20 \sqrt{2} \, \text{cm}\).
Triangle ABC is an isosceles triangle. The length of the base is 20 meters and the corresponding height is 24 meters. Find the perimeter of ABC. (Round your answer to the nearest tenth of a meter).
Solution
The isosceles triangle ABC is shown below. Height AM is drawn. Triangles AMB and AMC are congruent since they have two congruent sides AB and AC and AM is common. Also, angles B and C are equal in measure and the right angles at M are equal. Hence, the lengths of AM and CM are equal, and therefore the length of MC is equal to 10 meters.
We now use Pythagoras' theorem to find length \(x\) of side AB:
\[ x^2 = 24^2 + 10^2 = 576 + 100 = 676 \] \[ x = \sqrt{676} = 26 \text{ meters}. \]The perimeter of the triangle is:
\[ \text{Perimeter} = AB + AC + BC = 26 + 26 + 20 = 72 \text{ meters}. \]A triangle has an area of 90 square cm. Find the length of the base if the base is 3 cm more than the height.
Solution
Let \(b\) be the length of the base and \(h\) the height. The area \(A\) of the triangle is:
\[ A = \frac{1}{2} \times b \times h = 90. \]Given:
\[ b = h + 3. \]Substitute \(b = h + 3\) into the area formula:
\[ \frac{1}{2} (h + 3) h = 90. \]Multiply both sides by 2:
\[ (h + 3) h = 180. \]Expand:
\[ h^2 + 3h = 180. \]Rewrite as a quadratic equation:
\[ h^2 + 3h - 180 = 0. \]Factor:
\[ (h - 12)(h + 15) = 0. \]So:
\[ h = 12 \quad \text{(since height must be positive)}. \]Calculate base:
\[ b = 12 + 3 = 15 \text{ cm}. \]The perimeter of a triangle is 74 inches. The length of the first side is twice the length of the second side. The third side is 4 inches more than the first side. Find the length of each side.
Solution
Let \(x\) be the length of the second side. Then:
\[ \text{First side} = 2x, \] \[ \text{Third side} = 2x + 4. \]The perimeter is:
\[ 2x + x + (2x + 4) = 5x + 4 = 74. \]Solve for \(x\):
\[ 5x = 70, \] \[ x = 14. \]Lengths of sides are:
\[ \text{Side 1} = 2x = 28 \text{ inches}, \] \[ \text{Side 2} = x = 14 \text{ inches}, \] \[ \text{Side 3} = 2x + 4 = 28 + 4 = 32 \text{ inches}. \]Determine the area of the triangle enclosed by the lines \(y = -4\), \(x = 1\), and \(y = -2x + 8\).
Solution
The triangle has vertices at the intersections of the lines. To find its area, find the base and height lengths by locating points A, B, and C.
Find point \(A\) by intersecting \(x=1\) and \(y=-2x + 8\):
\[ x=1 \implies y = -2(1) + 8 = 6. \] \[ A = (1, 6). \]Find point \(B\) by intersecting \(y = -4\) and \(y = -2x + 8\):
\[ -4 = -2x + 8 \implies -2x = -12 \implies x = 6. \] \[ B = (6, -4). \]The height \(AB\) is vertical distance:
\[ AB = |6 - (-4)| = 10. \]The base \(BC\) is horizontal distance between \(B\) and \(C\), where \(C\) lies on \(x=1\) and \(y=-4\):
\[ C = (1, -4), \] \[ BC = |6 - 1| = 5. \]The area \(A\) is:
\[ A = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times 10 \times 5 = 25 \text{ square units}. \]Show that the triangle with vertices \(A(-1,6)\), \(B(2,6)\), and \(C(2,2)\) is a right triangle and find its area.
Solution
Calculate squared lengths of sides:
\[ AB^2 = (2 - (-1))^2 + (6 - 6)^2 = 3^2 + 0^2 = 9, \] \[ BC^2 = (2 - 2)^2 + (2 - 6)^2 = 0^2 + (-4)^2 = 16, \] \[ CA^2 = (-1 - 2)^2 + (6 - 2)^2 = (-3)^2 + 4^2 = 9 + 16 = 25. \]Check Pythagoras' theorem:
\[ CA^2 = AB^2 + BC^2 \implies 25 = 9 + 16. \]Since the equality holds, triangle ABC is right-angled with hypotenuse \(CA\).
The area \(A\) is:
\[ A = \frac{1}{2} \times AB \times BC = \frac{1}{2} \times 3 \times 4 = 6 \text{ square units}. \]