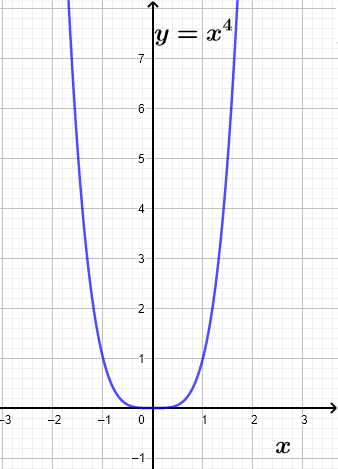
About: Polynomial of the fourth degree: touches the x axis at one point.
Question: Why does the graph touches (but not cut) the x-axis at one point only?
Several fourth degree polynomials are presented along with questions with detailed solutions.
Question 1
About: Polynomial of the fourth degree: touches the x axis at one point.
Question: Why does the graph touches (but not cut) the x-axis at one point only?

Question 2
About: Polynomial of the Fourth degree: 2 x-intercepts.
Question: If the graph cuts the x axis at x = 1, what are the coordinates of the other x-intercpet?

Question 3
About: Polynomial of the Fourth degree: 3 x-intercepts and parameter \( a \) to determine.
Question: The graph below touches (but does not cut) the x-axis at x = 2. What are the coordinates of the other two x-intercpets?

Question 4
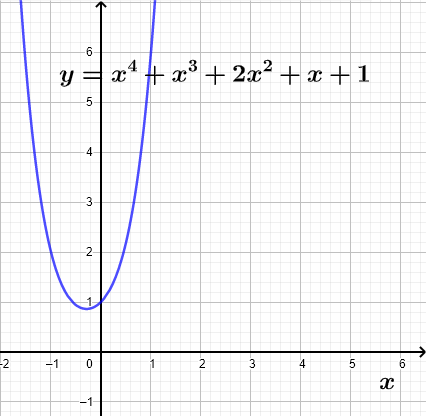
About: Polynomial of a fourth degree: no x-intercepts.
Question: Why does the graph of the fourth degree polynomial \( y = x^4+x^3+2x^2+x+1 \) have no x-intercept knowing that \( x^2 + 1 \) is a factor of this polynomial?
Answer Question 1
Examine the equation of the polynomial given: \( y = x^4 \). Solve \( x^4 = 0 \) to obtain a zero of multiplicity
4, hence the the graph touches the x-axis at one point but the graph is flat at \( x = 0 \) indicating the mutliplicity \( 4 \) .
Answer Question 2
An x intercept at \( x = 1\) means that \( x - 1 \) is a factor of the given polynomial and we can write: \( y = x^4+0.5x-x^3-0.5\) = (x-1) Q(x) \).
Using polynomial division to find: \( Q(x) = \dfrac{x^4+0.5x-x^3-0.5}{x-1} = x^3+0.5 \) and therefore the given polynomial can be written as: \( y = (x - 1)(x^3+0.5) \).
Find the other zero(s) by solving \( x^3+0.5 = 0 \) which has one real solution given by \( x = - \sqrt[3]{0.5} \approx - 0.8 \) as shown in the graph above.
Answer Question 3
The graph of the polynomial touches the x-axis at \( x = 2 \) and therefore \( y = 0 \) for \( x = 2 \). Hence the equation
\( (2)^4-2(2)^3-5(2)^2+ a(2) - 4 = 0 \)
Simplify and solve for \( a \) to obtain \( a = 12 \)
Substitute \( a \) by \(12 \) to write the given polynomial as \( y = x^4-2x^3-5x^2+ 12 x-4 \)
Since the graph touches the x-axis at \( x = 2 \), \( x = 2 \) is a zero of an even multiplicity (2, 4, 6,...). The multipliciy cannot be more than \( 2 \) since the maximum number of zeros is no more than the degree of the polynomial which \( 4 \) and the graph has two other x-intercepts.
Therefore the polynomial \( y = x^4-2x^3-5x^2+ 12 x-4 \) may be written as \( y = (x-2)^2 Q(x) \) where \( Q(x) = \dfrac{x^4-2x^3-5x^2+ 12 x-4}{(x-2)^2}\) and using polynomial division, we obtain
\( Q(x) = x^2+2x-1 \)
The two remaining zeros are found by solving
\( x^2+2x-1 = 0 \)
which gives the solution \( x = -1+\sqrt{2} \approx 0.41 \) and \( x= - 1 - \sqrt{2} \approx -2.41 \) that are shown in the given graph of the polynomial.
Answer Question 4
Since \( x^2 + 1 \) is a factor of the given polynomial, this polynomial may be written in factored form as
\( x^4+x^3+2x^2+x+1 = (x^2+1) Q(x) \)
\( Q(x) \) is obtained by dividing numerator and denominator to obtain
\( Q(x) = \dfrac{x^4+x^3+2x^2+x+1}{x^2+1} = x^2+x+1 \)
The given polynomial may be written as
\( y = (x^2+1) (x^2+x+1 ) \)
The x-intercepts corresond to real zeros the polynomial that are obtained by solving
\( (x^2+1) (x^2+x+1 ) = 0 \)
\( x^2+1 = 0 \) has no real solutions.
\( x^2+x+1 = 0 \) has no real solution since it is a quadratic equation wih discriminant \( \Delta = (1)^2 - 4 \cdot 1 \cdot 1 = - 3 \) negative.
The given polynomial has no real zeros and therefore no x-intercepts.