Os quartis dividem um determinado conjunto de dados de números reais x1, x2, x3 ... xN em quatro grupos, classificados em ordem crescente, e cada grupo inclui aproximadamente 25% (ou um quarto) de todos os valores de dados incluídos no conjunto de dados.
Seja Q1 o quartil inferior, Q2 a mediana e Q3 o quartil superior. Os quatro grupos de valores de dados são definidos pelos intervalos:
Grupo 1: Do valor mínimo dos dados até Q1, Q1 também é chamado de 25º percentil porque 25% dos valores de dados no conjunto de dados estão abaixo de Q1
Grupo 2: De Q1 a Q2, Q2 também é chamado de percentil 50 porque 50% dos valores de dados no conjunto de dados estão abaixo de Q2
Grupo 3: Do 2º ao 3º trimestre, o 3º trimestre também é chamado de percentil 75 porque 75% dos valores de dados no conjunto de dados estão abaixo do 3º trimestre
Grupo 4: Do terceiro trimestre ao valor máximo dos dados.
Métodos de cálculo de quartis
Existem diferentes métodos para calcular os quartis. Dois métodos, que diferem apenas se o número de valores de dados for ímpar, serão descritos e usados.
Para ambos os métodos, você começa encontrando a mediana que é Q2.
Em seguida, você divide o conjunto de dados ordenado em duas metades: uma metade inferior e uma metade superior. Se o número de valores de dados N for par, a divisão será direta. No entanto, se H for ímpar, existem dois métodos para criar as duas metades Primeiro método
Divida o conjunto de dados em duas metades sem incluir a mediana. O quartil inferior Q1 é a mediana da metade inferior e o quartil superior é a mediana da metade superior. Segundo método
Divida o conjunto de dados em duas metades, incluindo a mediana em ambas as metades
O quartil inferior Q1 é a mediana da metade inferior e o quartil superior é a mediana da metade superior.
Exemplos de cálculo de quartis e desenho de box plot
Exemplo 1
Calcule os quartis do conjunto de dados: 20 , 2 , 1 , 12 , 4 , 8 , 9 , 6 e desenhe o box plot. Solução para o Exemplo 1
Primeiro ordenamos o conjunto de dados em ordem crescente
1 , 2 , 4 , 6 , 8 , 9 , 12 , 20
Encontre a mediana Q2 do conjunto de dados fornecido: Q2 = (6 + 8) / 2 = 7
O número N de valores de dados é igual a 8 e, portanto, par; dividimos o conjunto de dados em duas metades
metade inferior: 1 , 2 , 4 , 6
Metade superior: 8 , 9 , 12 , 20
O quartil inferior Q1 é igual à mediana da metade inferior; portanto
Q1 = (2 + 4) / 2 = 3
O quartil superior Q3 é igual à mediana da metade superior; portanto
Q3 = (9 + 12) / 2 = 10,5
Os quartis, os valores mínimo e máximo dos dados são plotados juntos junto com os valores dos dados (em azul) para criar o que é chamado de box plot conforme mostrado abaixo. O conjunto de dados é dividido em quatro grupos conforme descrito acima, com os dois grupos no meio de Q1 a Q3 formando a caixa e os grupos externos do mínimo a Q1 e de Q3 ao máximo formando os bigodes.
Grupo 1: Do valor mínimo dos dados até o primeiro trimestre
Grupo 2: Do 1º ao 2º trimestre
Grupo 3: Do 2º ao 3º trimestre
Grupo 4: Do terceiro trimestre ao valor máximo dos dados.
Podemos facilmente verificar se cada grupo contém 2 valores de dados de um total de 8, o que representa um quarto ou 25% dos valores dos dados.
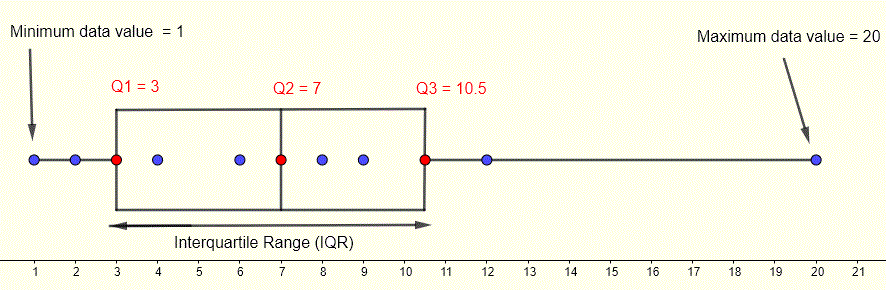
Os gráficos de caixa são um resumo de cinco números que inclui os valores mínimo e máximo dos dados, a mediana e os quartis inferior e superior. Eles podem ser úteis para entender como os dados são distribuídos em um determinado conjunto e fornecer informações qualitativas sobre a distribuição dos dados.
Exemplo 2
As notas de uma turma em um exame de matemática são: 55, 35, 60, 86, 65, 75, 83, 88, 88, 90, 95, 96, 98. Calcule os quartis das notas e desenhe um box plot.< br>
Solução para o Exemplo 2
Primeiro ordenamos o conjunto de dados em ordem crescente
35, 55, 60, 65, 75, 83, 86, 88, 88, 90, 95, 96, 98
Encontre a mediana Q2 do conjunto de dados fornecido: Q2 = 86
O número N de valores de dados é igual a 13 e, portanto, ímpar; usaremos os dois métodos descritos acima. Método 1: Divida as pontuações em duas metades, incluindo a mediana 86
metade inferior: 35, 55, 60, 65, 75, 83, 86
Metade superior: 86, 88, 88, 90, 95, 96, 98
O quartil inferior Q1 é igual à mediana da metade inferior; portanto
Q1 = 65
O quartil superior Q3 é igual à mediana da metade superior; portanto
3º trimestre = 90
Os quartis e os valores mínimo e máximo dos dados são plotados juntos para criar o que é chamado de box plot conforme mostrado abaixo. O conjunto de dados é dividido em quatro grupos conforme descrito acima
Método 2: Divida as pontuações em duas metades, sem incluir a mediana 86
metade inferior: 35, 55, 60, 65, 75, 83
Metade superior: 88, 88, 90, 95, 96, 98
O quartil inferior Q1 é igual à mediana da metade inferior;
Q1 = (60 + 65) / 2 = 62,5
O quartil superior Q3 é igual à mediana da metade superior; portanto
Q3 = (90 + 95) / 2 = 92,5
Os box plots com quartis, os valores mínimo e máximo dos dados são plotados abaixo para os dois métodos.
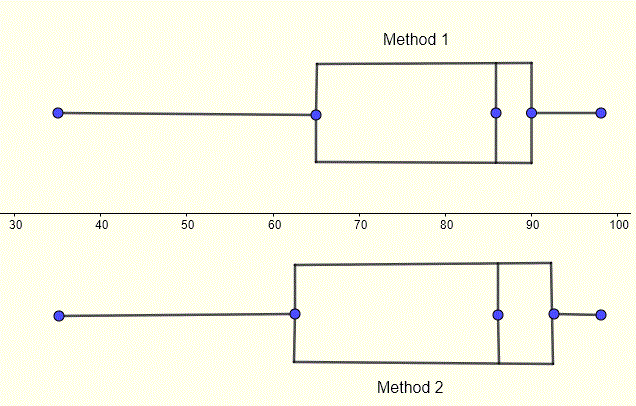
Exemplos de leitura de quartis em gráficos de caixa
Exemplo 3
Os box plots das notas em um exame das classes A, B, C e D são mostrados abaixo. O número de alunos em cada uma das classes A, B, C e D é 12, 19, 22 e 28 respectivamente.
Use os gráficos de caixa para responder às seguintes perguntas
a) Determinar as pontuações mínimas e máximas, os quartis inferior e superior, a mediana, o intervalo e o intervalo interquartil (IQR) de cada classe.
b) Qual turma tem a pontuação mais alta?
c) Qual turma tem a pontuação mais baixa?
d) Quantos alunos pontuaram acima da mediana em cada turma?
e) Quantos alunos pontuaram abaixo do quartil inferior em cada turma?
f) Quantos alunos pontuaram o quartil inferior e o máximo em cada turma?
g) Utilizando o intervalo e os intervalos interquartis, qual classe tem a maior dispersão e qual classe tem a menor dispersão de pontuações? Solução do Exemplo 3
a)
Intervalo = valor máximo dos dados - valor mínimo dos dados
Intervalo interquartil (IQR) = Q3 - Q1
minimum
maximum
Q1
Q3
Q2
Range
IQR
Class A
50
94
64
90
85
44
26
Class B
20
100
60
94
76
80
34
Class C
41
98
65
90
85
57
25
Class D
30
98
60
90
82
68
30
b)
A classe B tem a pontuação mais alta de 100
c)
A classe B tem a pontuação mais baixa, 20
d)
A mediana divide as pontuações ordenadas em duas metades e, portanto, metade das pontuações da turma acima da mediana
turma A: (1/2) total = (1/2) 12 = 6 alunos
turma B: (1/2) total = (1/2) 19 = 9,5, arredondado para 10 alunos (o número de alunos deve ser um número inteiro)
turma C: (1/2) total = (1/2) 22 = 11 alunos
turma D: (1/2) total = (1/2) 28 = 14 alunos
e)
Quartis divide o conjunto de dados (pontuações neste exemplo) em 4 grupos com 1/4 cada. Assim, para cada turma, um quarto das pontuações estão abaixo do quartil inferior
turma A: (1/4) total = (1/4) 12 = 3 alunos
turma B: (1/4) total = (1/4) 19 = 4,75, arredondado para 5 alunos (o número de alunos deve ser um número inteiro)
turma C: (1/4) total = (1/4) 22 = 5,5, arredondado para 6 alunos (o número de alunos deve ser um número inteiro)
turma D: (1/4) total = (1/4) 28 = 7 alunos
f)
Quartis divide o conjunto de dados (pontuações neste exemplo) em 4 grupos com 1/4 cada. Assim, para cada turma, 3/4 quartos das pontuações estão entre o quartil inferior e o máximo (ou acima do quartil inferior)
turma A: (3/4) total = (3/4) 12 = 9 alunos
turma B: (3/4) total = (3/4) 19 = 14,25, arredondado para 14 alunos (o número de alunos deve ser um número inteiro)
turma C: (3/4) total = (3/4) 22 = 16,5, arredondado para 17 alunos (o número de alunos deve ser um número inteiro|)
g)
A classe A possui o menor intervalo e intervalo interquartil; 44 e 26 respectivamente.
A classe B possui o maior alcance e intervalo interquartil; 80 e 34 respectivamente.
Utilizando os box plots e a amplitude e intervalo interquartil, podemos concluir que as pontuações da classe A apresentam a menor dispersão e as pontuações da classe B apresentam a maior dispersão.
