O desvio padrão é uma medida de quão próximos os valores dos dados em um conjunto de dados estão da média. É uma quantidade pequena quando os dados são distribuídos perto da média e grande quando os dados estão longe da média.
seja x1, x2, x3 ... xN seja um conjunto de dados com média μ. Para medir a que distância um valor de dados xi está da média, podemos usar a diferença d eu dado por di = xi - μ
O problema com a definição acima é que di pode ser negativo ou positivo e quando você adiciona todos os d< sub>i para todos os valores de dados para obter uma média, eles podem se cancelar. Portanto, elevamos ao quadrado di, calculamos a média e calculamos a raiz quadrada.
O desvio padrão σ de uma população com N elementos é definida por
Num estudo estatístico, podemos ter grandes populações e, portanto, calcular o desvio padrão para toda a população pode ser dispendioso e demorado, daí a ideia de usar amostras da população para estimar o desvio padrão.
O desvio padrão s de um conjunto de dados de uma amostra com N elementos é definido por
A principal diferença entre as duas fórmulas é a divisão por N e N - 1. Usamos N - 1 na fórmula do desvio padrão para amostras para compensar o fato de que o número de valores de dados em uma população é muito maior que o número de valores de dados em uma amostra. Observe também que para N muito grande, as duas fórmulas dariam valores muito próximos.
Uma calculadora on-line para calcular o desvio padrão está incluída.
Exemplos de desvio padrão
Exemplo 1
Três conjuntos de dados representando três populações são fornecidos abaixo.
R:{1,1,15,15} B:{1,7,9,15} C:{7,7,9,9}
Calcule a média e o desvio padrão para cada conjunto de dados. Compare as médias e o desvio padrão dos três conjuntos. Solução do Exemplo 1
Para o conjunto A
\[\mu_A = \dfrac{1 + 1 + 15 + 15 + 11}{4} = 8\]
\[\sigma_A=\sqrt {\dfrac{(1 - 8)^2 + (1 - 8)^2 + (15 - 8)^2 + (15 - 8)^2}{4}} = 7\]
Para o conjunto B
\[\mu_B = \dfrac{1 + 7 + 9 + 15}{5} = 8\]
\[\sigma_B =\sqrt {\dfrac{(1 - 8)^2 + (7 - 8)^2 + (9 - 8)^2 + (15 - 8)^2}{4}} = 5\]
Para o conjunto C
\[\mu_C = \dfrac{7 + 7 + 9 + 9}{4} = 8\]
\[\sigma_C =\sqrt {\dfrac{(7 - 8)^2 + (7 - 8)^2 + (9 - 8)^2 + (9 - 8)^2}{4}} = 1\]
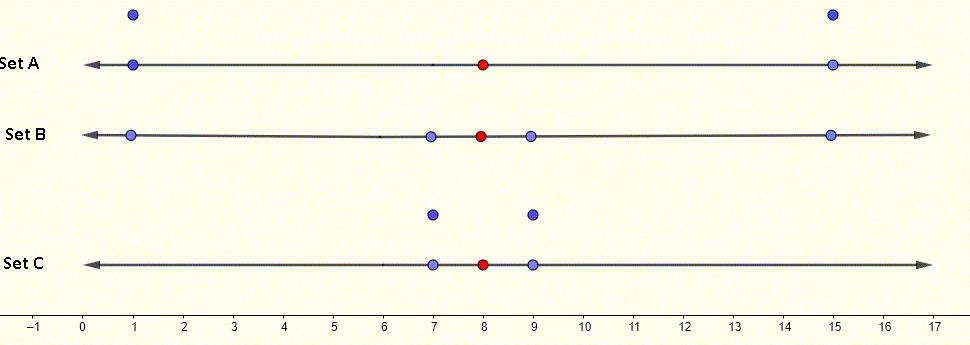
As médias dos três conjuntos são iguais a 8 (ponto vermelho no gráfico) e os desvios padrão são diferentes. Podemos ver nos gráficos das retas numéricas abaixo dos três conjuntos. É graficamente claro que os valores dos dados no Conjunto C estão próximos da média e é por isso que este conjunto apresenta o menor desvio padrão. Os gráficos na reta numérica do conjunto A e B mostram que os dados do conjunto A são mais dispersos do que os dados do conjunto B, portanto, o desvio padrão do conjunto A é maior que o do conjunto B.
Exemplo 2
Dois conjuntos de dados representando duas populações são fornecidos abaixo.
R:{2 , 3 , 5 , 8 , 10} B:{3, 4, 6, 9, 11}
Calcule a média e o desvio padrão para cada conjunto de dados. Compare as médias e o desvio padrão dos dois conjuntos. Solução para o Exemplo 2
Para o conjunto A
\[\mu_A = \dfrac{2 + 3 + 5 + 8 + 10}{5} = 5,6\]
\[\sigma_A=\sqrt {\dfrac{(2 - 5,6)^2 + (3 - 5,6)^2 + (5 - 5,6)^2 + (8 - 5,6)^2 + (10 - 5,6)^2 }{5}}\]
\[=3,0\]
Para o conjunto B
\[\mu_B = \dfrac{3 + 4 + 6 + 9 + 11}{5} = 6,6\]
\[\sigma_B =\sqrt {\dfrac{(2 - 5,6)^2 + (3 - 5,6)^2 + (5 - 5,6)^2 + (8 - 5,6)^2 + (10 - 5,6)^2 }{5}}\]
=3.0
As médias são diferentes e os desvios padrão são iguais. Isso significa que os valores dos dados nos dois conjuntos são distribuídos da mesma maneira em torno da média. Os dois conjuntos A e B são mostrados abaixo nas retas numéricas. Embora os dois conjuntos sejam diferentes, as distâncias entre os valores dos dados e a média são correspondentemente iguais e isso explica porque os dois conjuntos têm desvios padrão iguais.
Exemplo 3
As notas em uma prova de Física dos alunos das duas turmas A e B têm as seguintes médias e desvios padrão.
Classe A: média = 78 e desvio padrão = 5
Classe A: média = 78 e desvio padrão = 15
O que podemos concluir sobre o desempenho dos alunos nas duas turmas? Solução do Exemplo 3
As notas das duas turmas têm médias iguais, mas o desvio padrão da turma B é maior que o desvio padrão da turma A. Isso significa que as pontuações na turma B são mais dispersas e, portanto, na turma B e, portanto, alguns alunos podem ter pontuado muito inferior à média, enquanto outros alunos podem ter pontuado muito mais alto do que a média. Em geral, os alunos da classe A obtiveram pontuações mais próximas da média.
Exemplo 4
A média de um conjunto de valores de dados é igual a μ e seu desvio padrão é igual a σ. Se todos os valores de dados no conjunto forem aumentados pelo mesmo valor k, qual é a média e o desvio padrão após o aumento? Solução para o Exemplo 4
Se você plotar todos os valores de dados em uma reta numérica e adicionar k a esses valores e representá-los novamente na mesma reta numérica, todos os pontos na reta numérica seriam deslocados na mesma distância k e, portanto, a média também aumentaria em k. No entanto, o desvio padrão não mudará porque é uma medida da distância entre os valores dos dados e a média e todos eles foram deslocados pelo mesmo valor k.
A média e o desvio padrão do conjunto { x_1, x_2 ,... x_N } são dados por
\[\mu = \dfrac{\sum_{i=1}^{N} x_i}{N}\]
e
\[\sigma =\sqrt {\dfrac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}}\]
Agora adicionamos k a cada valor de dados x_i e calculamos a média e o desvio padrão
\[\mu_k = \dfrac{\sum_{i=1}^{N} (x_i + k)}{N} = \dfrac{\sum_{i=1}^{N} x_i}{N} + \dfrac{\sum_{i=1}^{N} k}{N} = \mu + k\]
\[\sigma_k =\sqrt {\dfrac{\sum_{i=1}^{N} ((x_i + k) - \mu_A)^2}{N}} = \sqrt {\dfrac{\sum_{i =1}^{N} (x_i + k - (\mu + k))^2}{N}}\]
Simplifique o numerador para obter
\[\sigma_k = \sqrt {\dfrac{\sum_{i=1}^{N} (x_i - \mu )^2}{N}}\]
Portanto, se aumentarmos todos os valores de dados em um conjunto na mesma quantidade k, a média aumenta em k, mas o desvio padrão não muda.
