Dominio de una Función de Raíz Cuadrada
Cómo encontrar el dominio de funciones de raíz cuadrada? Se presentan varios ejemplos junto con soluciones y explicaciones detalladas, con interpretaciones gráficas del dominio.
Encontrar el Dominio de una Función de Raíz Cuadrada
Primero debemos entender que \( \sqrt x \) es real solo si el argumento \( x \) (la cantidad bajo el radical \( \sqrt{} \)) satisface la condición: \( x \ge 0 \). Esto se puede verificar fácilmente examinando la gráfica de \( y = \sqrt x \) que se muestra a continuación: La gráfica existe solo para \( x \ge 0 \).

Ejemplos con sus Soluciones
Ejemplo 1
Encuentra el dominio de la función \[ f(x) = \sqrt{x - 2} \]
Solución
\( f(x) = \sqrt{x - 2} \) toma valores reales si el argumento \( x - 2 \) (la cantidad bajo el radical \( \sqrt{} \)) satisface la condición: \( x - 2 \ge 0 \). La solución de la desigualdad es
\[ x \ge 2 \]
que es el dominio de la función. Esto se puede verificar gráficamente como se muestra a continuación, donde la gráfica de \( f \) "existe" para \( x \ge 2 \).

Ejemplo 2
Encuentra el dominio de la función \[ f(x) = \sqrt{|x - 1|} \]
Solución
\( f(x) = \sqrt{|x - 1|} \) toma valores reales si el argumento \( |x - 1| \) (la cantidad bajo el radical \( \sqrt{} \)) satisface la condición: \( |x - 1| \ge 0 \). La solución de la desigualdad son todos los números reales, porque la expresión de valor absoluto \( |x - 1| \) siempre es positiva o cero (para \( x = 1 \)).
El dominio de la función es el conjunto de los números reales \( \mathbb{R} \), y esto se puede verificar gráficamente como se muestra a continuación, donde la gráfica de \( f \) "existe" para todos los valores de \( x \).

Ejemplo 3
Encuentra el dominio de la función \[ f(x) = \dfrac{1}{ \sqrt{x + 3}} \].
Solución
Teniendo en cuenta que la función es el cociente de dos funciones y que la división por cero no está permitida, la función dada toma valores reales si el argumento \( x + 3 \) (la cantidad bajo el radical \( \sqrt{} \)) satisface la condición: \( x + 3 \gt 0 \). Nota: el símbolo de desigualdad utilizado es \( \gt \) y no \( \ge \) porque no queremos tener cero en el denominador. La solución de la desigualdad es
\[ x \gt - 3 \]
El dominio de la función es el conjunto de números reales mayores que -3, y esto se puede verificar gráficamente como se muestra a continuación, donde la gráfica de \( f \) "existe" para todos los valores \( x > - 3 \).

Ejemplo 4
Encuentra el dominio de la función \[ f(x) = \dfrac{\sqrt{x + 4}}{ \sqrt{x - 2}} \]
Solución
La función dada toma valores reales si se satisfacen dos condiciones.
1) \( x + 4 \ge 0 \) (se permite cero en el numerador, de ahí el uso del símbolo de desigualdad \( \ge \)).
y
2) \( x - 2 \gt 0 \) (NO se permite cero en el denominador, de ahí el uso del símbolo de desigualdad \( \gt \)).
El dominio de la función es la intersección de los dos conjuntos solución de las dos desigualdades anteriores.
\[ x \ge - 4 \quad \text{y} \quad x \gt 2 \]
La intersección de los dos conjuntos solución anteriores es:
\[ x \gt 2 \]
Que es el dominio de la función dada, como se muestra en la gráfica de \( f \) a continuación.

Ejemplo 5
Encuentra el dominio de la función \( f(x) = \sqrt{\dfrac{x + 4}{ {x - 2}}} \).
Solución
La función dada toma valores reales si
\[ \dfrac{x + 4}{ {x - 2}} \ge 0 \]
Necesitamos resolver la desigualdad anterior. Los ceros del numerador y del denominador son
\[ x = - 4 \quad \text{y} \quad x = 2 \]
Los ceros dividen la recta numérica en 3 intervalos sobre los cuales el signo de la desigualdad es el mismo. Los intervalos son:
\[ (-\infty , -4) \; , \; (-4 , 2 ) \; , \; (2 , \infty) \]
Seleccionamos un valor dentro de cada intervalo y lo usamos para encontrar el signo de la expresión \[ \dfrac{x + 4}{ {x - 2}} \].
1) En el intervalo \( (-\infty , -4) \), seleccionamos \( x = -6 \) y sustituimos \( x \) por \( -6 \) en \( \dfrac{x + 4}{ {x - 2}} \) para determinar su signo:
\[ \dfrac{ -6 + 4}{ {-6 - 2}} \gt 0 \]
2) En el intervalo \( (-4 , 2) \), seleccionamos \( x = 0 \) y sustituimos \( x \) por \( 0 \) en \( \dfrac{x + 4}{ {x - 2}} \) para determinar su signo:
\[ \dfrac{ 0 + 4}{ {0 - 2}} \lt 0 \]
3) En el intervalo \( (2 , \infty) \), seleccionamos \( x = 3 \) y sustituimos \( x \) por \( 3 \) en \( \dfrac{x + 4}{ {x - 2}} \) para determinar su signo:
\[ \dfrac{ 3 + 4}{ {3 - 2}} \gt 0 \]
Por lo tanto, el dominio es la unión de todos los intervalos sobre los cuales \( \dfrac{x + 4}{ {x - 2}} \gt 0 \), y está dado por:
\[ (-\infty , -4] \cup (2 , \infty) \]
La gráfica de \( f \) se muestra a continuación y podemos verificar fácilmente el dominio encontrado. Nota: \( x = 2 \) no está en el dominio porque no se permite la división por cero.

Ejemplo 6
Encuentra el dominio de la función \[ f(x) = \sqrt{-x^2-4} \]
Solución
La función dada toma valores reales si
\[ -x^2 - 4 \ge 0 \]
La expresión \( x^2 + 4 \) es la suma de un cuadrado y un número positivo. Por lo tanto,
\[ x^2 + 4 \ge 0 \]
Multiplicamos todos los términos de la desigualdad anterior por -1 y cambiamos el símbolo de desigualdad para obtener:
\[ - x^2 - 4 \le 0 \]
Por lo tanto, el dominio de la función dada es un conjunto vacío y la función dada no tiene gráfica. Intenta graficarla usando una calculadora gráfica.
Ejemplo 7
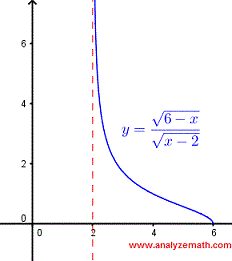
Encuentra el dominio de la función \[ f(x) = \dfrac{\sqrt{6 - x}}{ \sqrt{x - 2}} \]
Solución
La función dada toma valores reales si se satisfacen dos condiciones.
1) \( 6 - x \ge 0 \) (se permite cero en el numerador, de ahí el uso de \( \ge \)).
y
2) \( x - 2 \gt 0 \) (no se permite cero en el denominador, de ahí el uso de \( \gt \)).
El dominio de la función es la intersección de los dos conjuntos solución de las dos desigualdades anteriores:
\[ x \le 6 \quad \text{y} \quad x \gt 2 \]
La intersección de los dos conjuntos solución anteriores está dada por el intervalo:
\[ (2 , 6] \]
La gráfica de \( f \) se muestra a continuación y podemos verificar fácilmente el dominio encontrado. Nota: \( x = 2 \) no está en el dominio porque no se permite la división por cero.
Ejemplo 8
Encuentra el dominio de la función \[ f(x) = \sqrt{x^2 - 4} \]
Solución
La función dada toma valores reales si
\[ x^2 - 4 \ge 0 \] que también se puede escribir como \[ (x - 2)(x + 2) \ge 0 \]
El conjunto solución de la desigualdad cuadrática anterior está dado por el intervalo:
\[ (-\infty , -2] \cup [2 , \infty) \]
La gráfica de \( f \) se muestra a continuación y podemos verificar fácilmente el dominio encontrado.

Ejemplo 9
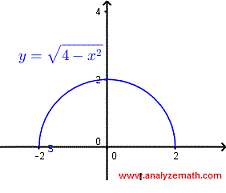
Encuentra el dominio de la función \( f(x) = \sqrt{4 - x^2} \).
Solución
La función dada toma valores reales si
\[ 4 - x^2 \ge 0 \] que también se puede escribir como \[ (2 - x)(2 + x) \ge 0 \]
El conjunto solución de la desigualdad cuadrática anterior está dado por el intervalo:
\[ [-2 , 2] \]
La gráfica de \( f \) se muestra a continuación y podemos verificar fácilmente el dominio encontrado.
Más Referencias y Enlaces









