Preguntas y Problemas de Parábolas con Soluciones Detalladas
Explora una colección de problemas de parábolas. Se incluyen soluciones detalladas con explicaciones para ayudar a profundizar tu comprensión.
Problema 1
Encuentra las intersecciones con los ejes x e y, el vértice y el eje de simetría de la parábola con ecuación \( y = - x^2 + 2 x + 3 \).
Las intersecciones con el eje x son los puntos donde la parábola corta el eje x, por lo que sus coordenadas y son iguales a 0. Resolvemos:
\[ 0 = - x^2 + 2x + 3 \]
Factorizando: \[ -(x - 3)(x + 1) = 0 \]
Soluciones: \[ x = 3 \quad \text{y} \quad x = -1 \].
La intersección con el eje y es el punto donde x=0:
\[ y = - (0)^2 + 2 (0) + 3 = 3 \].
Para el vértice, completamos el cuadrado:
\[ y = - x^2 + 2 x + 3 = -(x^2 - 2x - 3) = -( (x - 1)^2 - 4) = -(x - 1)^2 + 4 \]
Vértice en \[ (1 , 4) \].
Eje de simetría: \[ x = 1 \].
Verifica estos puntos en la gráfica:

Problema 2
¿Cuáles son los puntos de intersección de la recta \( 2x + 3y = 7 \) con la parábola \( y = - 2 x^2 + 2 x + 5 \)?
Sustituimos \( y \) en la ecuación de la recta:
\[ 2x + 3(- 2x^2 + 2x + 5) = 7 \]
Simplificando: \[ -6x^2 + 8x + 8 = 0 \], dividimos entre 2: \[ -3x^2 + 4x + 4 = 0 \].
Soluciones: \[ x = 2, \quad x = -\frac{2}{3} \].
Sustituyendo en la recta:
Para \( x=2 \): \( y=1 \). Para \( x=-\frac{2}{3} \): \( y=\frac{25}{9} \).
Puntos de intersección: \[ (2,1) \quad \text{y} \quad (-\frac{2}{3}, \frac{25}{9}) \].
Verificación gráfica:

Problema 3
Encuentra los puntos de intersección de las parábolas \( y = -(x - 3)^2 + 2 \) y \( y = x^2 - 4x + 1 \).
Igualamos las ecuaciones:
\[ -(x - 3)^2 + 2 = x^2 - 4x + 1 \]
Expandiendo: \[ -x^2 + 6x - 9 + 2 = x^2 - 4x + 1 \rightarrow -2x^2 + 10x - 8 = 0 \].
Dividimos entre -2: \[ x^2 - 5x + 4 = 0 \].
Soluciones: \[ x = 1, \quad x = 4 \].
Sustituyendo: Para \( x=1 \), \( y=-2 \); para \( x=4 \), \( y=1 \).
Puntos de intersección: \[ (1,-2) \quad \text{y} \quad (4,1) \].
Verificación gráfica:
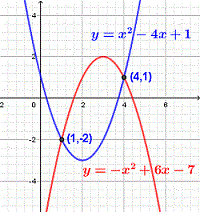
Problema 4
Encuentra la ecuación de la parábola \( y = 2 x^2 + b x + c \) que pasa por los puntos \( (-1,-5) \) y \( (2,10) \).
Sustituimos los puntos:
Para \( (-1,-5) \): \[ -5 = 2(1) + b(-1) + c \rightarrow -b + c = -7 \].
Para \( (2,10) \): \[ 10 = 8 + 2b + c \rightarrow 2b + c = 2 \].
Resolviendo el sistema: \( b=3, c=-4 \).
Ecuación: \[ y = 2 x^2 + 3 x - 4 \].
Problema 5
¿Cuál es la ecuación de la parábola con intersecciones en \( x = 2 \) y \( x = -3 \), y una intersección en \( y = 5 \)?
Usamos la forma factorizada: \[ y = a(x - 2)(x + 3) \].
Con la intersección en y (0,5): \[ 5 = a(0-2)(0+3) = -6a \rightarrow a = -\frac{5}{6} \].
Ecuación: \[ y = -\frac{5}{6}(x - 2)(x + 3) \].
Problema 6
Encuentra la ecuación de la parábola \( y = a x^2 + b x + c \) que pasa por \( (0,3) \), \( (1,-4) \) y \( (-1,4) \).
Sustituyendo:
De \( (0,3) \): \( c=3 \).
De \( (1,-4) \): \( a + b + 3 = -4 \rightarrow a + b = -7 \).
De \( (-1,4) \): \( a - b + 3 = 4 \rightarrow a - b = 1 \).
Resolviendo: \( a = -3, b = -4 \).
Ecuación: \[ y = -3x^2 - 4x + 3 \].
Problema 7
Encuentra la ecuación de la parábola, con eje de simetría vertical, tangente a la recta \( y = 3 \) en \( x = -2 \), y que pasa por \( (0,5) \).
El vértice es \( (-2,3) \) por la tangencia. Usamos la forma vértice: \[ y = a(x + 2)^2 + 3 \].
Sustituyendo \( (0,5) \): \[ 5 = a(0+2)^2 + 3 \rightarrow 4a = 2 \rightarrow a = \frac{1}{2} \].
Ecuación: \[ y = \frac{1}{2}(x + 2)^2 + 3 \].
Problema 8
¿Para qué valor de la pendiente \( m \) la recta \( y = m x - 3 \) es tangente a la parábola \( y = 3 x^2 - x \)?
Igualamos: \[ m x - 3 = 3 x^2 - x \rightarrow 3x^2 - (1+m)x + 3 = 0 \].
Para tangencia, el discriminante es cero: \[ \Delta = (1+m)^2 - 36 = 0 \].
Resolviendo: \[ (1+m)^2 = 36 \rightarrow m = 5 \quad \text{o} \quad m = -7 \].
Problema 9
¿Para qué valores del parámetro \( b \) la recta \( y = 2 x + b \) interseca a la parábola \( y = - x^2 - 2 x + 1 \) en dos puntos diferentes?
Igualamos: \[ 2x + b = - x^2 - 2x + 1 \rightarrow -x^2 - 4x + 1 - b = 0 \].
Para dos intersecciones, discriminante positivo: \[ \Delta = 20 - 4b > 0 \rightarrow b < 5 \].
Problema 10
Encuentra la ecuación \( y = a x^2 + x \) de la parábola tangente a la recta \( y = 3 x + 1 \).
Igualamos: \[ 3x + 1 = a x^2 + x \rightarrow a x^2 - 2x - 1 = 0 \].
Para tangencia: \[ \Delta = 4 + 4a = 0 \rightarrow a = -1 \].
Ecuación: \[ y = -x^2 + x \].
Problema 11
Desplaza la gráfica de \( y = x^2 \) 3 unidades a la izquierda, luego refleja el resultado en el eje x, y finalmente desplázala 4 unidades hacia arriba. ¿Cuál es la ecuación después de estas transformaciones?
Inicio: \( y = x^2 \).
Desplazar izquierda: \( y = (x+3)^2 \).
Reflejar en eje x: \( y = -(x+3)^2 \).
Desplazar arriba: \( y = -(x+3)^2 + 4 \).
Problema 12
¿Qué transformaciones convierten la gráfica de \( y = x^2 \) en la gráfica de \( y = - x^2 + 4 x + 6 \)?
Completamos el cuadrado: \( y = - (x-2)^2 + 10 \).
Pasos: Desplazar 2 unidades a la derecha: \( y = (x-2)^2 \).
Reflejar en eje x: \( y = -(x-2)^2 \).
Desplazar 10 unidades arriba: \( y = -(x-2)^2 + 10 \).
Problema 13
Escribe la ecuación de la parábola mostrada en la gráfica.

Método 1: Usando intersecciones en x (-5,0) y (-1,0):
\( y = a(x+1)(x+5) \).
Con intersección en y (0,-5): \( -5 = 5a \rightarrow a = -1 \).
Ecuación: \( y = - (x+1)(x+5) = -x^2 - 6x - 5 \).
Método 2: Usando el vértice (-3,4):
\( y = a(x+3)^2 + 4 \).
Con (0,-5): \( -5 = 9a + 4 \rightarrow a = -1 \).
Ecuación: \( y = -(x+3)^2 + 4 = -x^2 - 6x - 5 \).
Más Referencias y Enlaces
- Problemas de álgebra universitaria - ejemplo 9: Ecuación de parábolas.
- Problema de parábola con solución.
- Problemas de vértice e intersección de parábolas.
- Encuentra los puntos de intersección de una parábola con una recta.
- Matemáticas de Secundaria Básica (Grados 6, 7, 8, 9) - Preguntas y Problemas Gratuitos con Respuestas
- Matemáticas de Secundaria (Grados 10, 11 y 12) - Preguntas y Problemas Gratuitos con Respuestas
- Matemáticas Primarias (Grados 4 y 5) con Preguntas y Problemas Gratis con Respuestas
- Página de Inicio