Encuentra el Período de Funciones Trigonométricas - Matemáticas 12º Grado
Explora problemas de trigonometría de 12º grado sobre el cálculo del período de funciones trigonométricas a partir de una gráfica o fórmula. Cada pregunta incluye soluciones detalladas paso a paso y explicaciones para ayudarte a comprender los conceptos con claridad.
Pregunta 1 - Período de una Función Seno
La siguiente gráfica corresponde a una función trigonométrica de la forma \( y = a \sin(b x) \), con \( b \gt 0 \). Encuentra su período y el parámetro \( b\).

Localiza dos ceros que delimiten un ciclo completo o un número entero de ciclos. En este ejemplo, podemos ver que desde el cero en \( x = 0 \) hasta el cero en \( x = 1 \), hay dos ciclos. Por lo tanto, el período \( P \) es igual a: \[ P = \dfrac{1 - 0}{2} = \dfrac{1}{2} \] Ahora usamos la fórmula del período en términos de \( b \) y la igualamos al valor del período encontrado en la gráfica. \[ \dfrac{2\pi}{b} = \dfrac{1}{2} \] Despejamos \( b \): \[ b = 4\pi \]
Pregunta 2 - Otra Función Seno
Se muestra a continuación la gráfica de una función trigonométrica de la forma \( y = a \sin(b x) \), con \( b >0 \). Encuentra su período y el parámetro \( b \).

Hay un ciclo desde el cero en \( x = -\dfrac{\pi}{4} \) hasta el cero en \( x = \dfrac{\pi}{4} \). Por lo tanto, el período \( P \) está dado por: \[ P = \dfrac{\pi}{4} - \left(-\dfrac{\pi}{4}\right) = \dfrac{\pi}{2} \] Igualamos el valor del período encontrado en la gráfica a la fórmula anterior y despejamos \( b \). \[ \dfrac{\pi}{2} = \dfrac{2\pi}{b}, \quad b = 4 \]
Pregunta 3 - Función Coseno con Desplazamiento de Fase
La siguiente gráfica corresponde a una función trigonométrica de la forma \( y = a \cos(b x + c) \) con \( b \gt 0 \). Encuentra el período de esta función y el valor de \( b \).

Hay dos ceros que delimitan medio ciclo. Primero encontramos estos ceros.
Cero a la izquierda: \[ \dfrac{-\pi/4 - \pi/8}{2} = -\dfrac{3\pi}{16} \] Cero a la derecha: \[ \dfrac{0 + \pi/8}{2} = \dfrac{\pi}{16} \] Por lo tanto, medio período es igual a: \[ \dfrac{\pi}{16} - \left(-\dfrac{3\pi}{16}\right) = \dfrac{\pi}{4} \] Y un período completo \( P \) es igual a: \[ P = 2 \times \dfrac{\pi}{4} = \dfrac{\pi}{2} \] Igualamos el valor del período encontrado en la gráfica a la fórmula anterior y despejamos \( b \). \[ \dfrac{\pi}{2} = \dfrac{2\pi}{b}, \quad b = 4 \]
Pregunta 4 - Función Seno con Desplazamiento Vertical
La siguiente gráfica corresponde a una función trigonométrica de la forma \( y = a \sin(b x + c) + d \), y los puntos A y B son puntos máximo y mínimo respectivamente. Encuentra el período de esta función y el valor de \( b \), suponiendo \( b \gt 0 \).
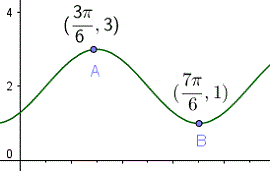
La distancia a lo largo del eje x entre los puntos A y B es igual a medio período y está dada por: \[ \dfrac{7\pi}{6} - \dfrac{3\pi}{6} = \dfrac{2\pi}{3} \] El período \( P \) de la función está dado por \[ P = 2 \times \dfrac{2\pi}{3} = \dfrac{4\pi}{3} \] \( b \) se encuentra resolviendo \[ \dfrac{2\pi}{b} = \dfrac{4\pi}{3}, \quad b = \dfrac{3}{2} \]
Pregunta 5 - Función Coseno con Mínimos Dados
Se muestra a continuación la gráfica de una función trigonométrica de la forma \( y = a \cos(b x + c) + d \), donde los puntos A y B son puntos mínimos con coordenadas x \( -0.3 \) y \( 0.1 \) respectivamente. Encuentra el valor de \( b \).

Hay un ciclo completo entre los puntos A y B. Por lo tanto, el período \( P \) está dado por \[ P = 0.1 - (-0.3) = 0.4 \] \( b \) se encuentra resolviendo \[ \dfrac{2\pi}{b} = 0.4, \quad b = 5\pi \]
Pregunta 6 - Período de Funciones Dadas
Encuentra el Período de Cada Una de las Siguientes Funciones
- \( y = \sin(x)\cos(x) - 3 \)
- \( y = 2 + 5\cos^2(x) \)
- \( y = \cos(x) + \sin(x) \)
- Usa la identidad \( \sin(2x) = 2 \sin(x) \cos(x) \): \[ y = \sin(x)\cos(x) - 3 = \dfrac{1}{2} \sin(2x) - 3 \] Período: \[ P = \dfrac{2\pi}{2} = \pi \]
- Usa la identidad \( \cos^2(x) = \dfrac{1}{2} (\cos(2x) + 1) \): \[ y = 2 + 5\cos^2(x) = 2 + 5\left(\dfrac{1}{2}(\cos(2x)+1)\right) = \dfrac{5}{2}\cos(2x) + \dfrac{9}{2} \] Período: \[ P = \dfrac{2\pi}{2} = \pi \]
- Reescribimos: \[ y = \cos(x) + \sin(x) = \dfrac{2}{\sqrt{2}}\left(\dfrac{\sqrt{2}}{2}\cos(x) + \dfrac{\sqrt{2}}{2}\sin(x)\right) \] Usando la identidad: \[ \sin\left(x+\dfrac{\pi}{4}\right) = \dfrac{\sqrt{2}}{2}\cos(x) + \dfrac{\sqrt{2}}{2}\sin(x) \] Entonces: \[ y = \sqrt{2}\,\sin\left(x + \dfrac{\pi}{4}\right) \] Período: \[ P = \dfrac{2\pi}{1} = 2\pi \]
Pregunta 7 - Regla General para el Período de \( f(kx) \)
Supón que \( f(x) \) es una función periódica con período \( p \). ¿Cuál es el período de la función \( h(x) = f(kx) \), donde \( k \) es una constante positiva?
Si \( p \) es el período de la función \( f \), entonces \[ f(x+p) = f(x) \quad \text{para todo } x \] Sea \( x = kX \), donde \( k \) es una constante: \[ f(kX+p) = f(kX) \] Reescribimos como: \[ f\left(k\left(X+\dfrac{p}{k}\right)\right) = f(kX) \] Sea \( h(x) = f(kx) \). Entonces: \[ h\left(X+\dfrac{p}{k}\right) = h(X) \] Esto indica que \( h(x) = f(kx) \) es periódica con período \[ \dfrac{p}{k} \]