¿Buscas entender cómo resolver ecuaciones logarítmicas? Esta guía completa proporciona soluciones claras y paso a paso a tipos comunes de problemas logarítmicos. Aprenderás a aplicar reglas y propiedades logarítmicas clave para resolver ecuaciones eficazmente.
\[ \log_b A + \log_b B = \log_b (AB) \] \[ \log_b A - \log_b B = \log_b \left( \dfrac{A}{B} \right) \] \[ \log_b \left( A^n \right) = n \log_b A \] \[ \text{Si } \log_b A = \log_b B, \text{ entonces } A = B \]
Además, la aproximación gráfica a las soluciones de ecuaciones de la forma \[ f(x) = g(x) \] se muestra como las intersecciones en x de la gráfica de la función \[ h(x) = f(x) - g(x) \].
Resuelve la ecuación: \[ \log(2x - 3) = \log(3 - x) - 2 \]
Reescribe la ecuación con los términos logarítmicos en un lado: \[ \log(2x - 3) - \log(3 - x) = -2 \] Sustituye \(-2\) por \(\log 10^{-2}\): \[ \log(2x - 3) - \log(3 - x) = \log 10^{-2} \] Usa la regla logarítmica \(\log A - \log B = \log \left(\dfrac{A}{B}\right)\): \[ \log\left( \dfrac{2x - 3}{3 - x}\right) = \log 10^{-2} \] Como la función \(\log(x)\) es uno a uno, deducimos: \[ \dfrac{2x - 3}{3 - x} = 10^{-2} \] Resolviendo: \[ 2x - 3 = \dfrac{3 - x}{100} \] \[ 200x - 300 = 3 - x \] \[ 201x = 303 \] \[ x = \dfrac{303}{201} = \dfrac{101}{67} \approx 1.51 \] Verificación: La ecuación tiene una solución \(x = \dfrac{101}{67} \approx 1.51\).
La intersección en x de la gráfica de \( q(x) = \log(2x - 3) - \log(3 - x) + 2 \) se muestra a continuación. Nota que la intersección en x se aproxima a la solución obtenida analíticamente.

Resuelve la ecuación: \[ \log x - \log(x^2 - 1) = -2 \log(x - 1) \]
Usa las reglas logarítmicas: \[ \log \left( \dfrac{x}{x^2 - 1}\right) = \log \left((x - 1)^{-2}\right) \] Dado que \(\log(x)\) es uno a uno: \[ \dfrac{x}{x^2 - 1} = (x - 1)^{-2} \] Multiplica por \((x - 1)^2\) y simplifica: \[ \dfrac{x(x - 1)}{x + 1} = 1 \] \[ x(x - 1) = x + 1 \] \[ x^2 - 2x - 1 = 0 \] Soluciones: \(x_1 = 1 + \sqrt{2} \approx 2.41\) y \(x_2 = 1 - \sqrt{2} \approx -0.41\). Verificación: Solo \(x_1\) es válida (el logaritmo de un número negativo no está definido). La solución es \(x_1 = 1 + \sqrt{2} \approx 2.41\).
La intersección en x de \(r(x) = \log x - \log(x^2 - 1) + 2 \log(x - 1)\) se muestra a continuación.

Resuelve la ecuación: \[ \log_2(2x - 9) = 2 - \log_2(x - 1) \]
Reescribe: \[ \log_2(2x - 9) + \log_2(x - 1) = \log_2 4 \] Usa la regla de la suma: \[ \log_2\left( (2x - 9)(x - 1) \right) = \log_2 4 \] \[ (2x - 9)(x - 1) = 4 \] \[ 2x^2 - 11x + 5 = 0 \] Soluciones: \(x_1 = \frac{1}{2}\) y \(x_2 = 5\). Verificación: Solo \(x_2 = 5\) es válida. La solución es \(x = 5\).
La solución gráfica se muestra como la intersección en x de \(s(x) = \log_2(2x - 9) - 2 + \log_2(x - 1)\).

Resuelve la ecuación: \[ 2 \ln(x + 3) - \ln(x + 1) = 3 \ln 2 \]
Usa las reglas logarítmicas: \[ \ln \left( \dfrac{(x + 3)^2}{x + 1} \right) = \ln 8 \] Dado que \(\ln x\) es uno a uno: \[ \dfrac{(x + 3)^2}{x + 1} = 8 \] \[ x^2 - 2x + 1 = 0 \] Solución: \(x = 1\). Verificación: La solución es válida.
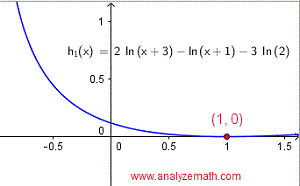
La solución gráfica se muestra como la intersección en x de \(h_1(x) = 2 \ln(x + 3) - \ln(x + 1) - 3 \ln 2\).
Resuelve la ecuación: \[ \left( \log_2(x) \right)^2 - \log_2(x^2) = 8 \]
Simplifica: \[ (\log_{2}(x))^{2} - 2 \log_{2}(x) = 8 \] Sea \(u = \log_{2}(x)\): \[ u^{2} - 2u - 8 = 0 \] Soluciones: \(u = -2\) y \(u = 4\). Luego, \(x = 2^{-2} = \frac{1}{4}\) y \(x = 2^{4} = 16\). Ambas soluciones son válidas.
Las soluciones gráficas se muestran como las intersecciones en x de \(p_{1}(x) = (\log_{2}(x))^{2} - \log_{2}(x^{2}) - 8\).

Resuelve la ecuación: \[ 10 \log(\log(x)) = 1 \]
Divide entre 10: \[ \log(\log(x)) = 0.1 \] \[ \log(x) = 10^{0.1} \] \[ x = 10^{10^{0.1}} \approx 18.15 \]
La solución gráfica se muestra como la intersección en x de \(f(x) = 10 \log(\log(x)) - 1\).
