Indeterminate forms of Limits

Examples with detailed solutions and exercises that solves limits questions related to indeterminate forms such as :
indeterminate forms of limits

Theorem

A second version of L'Hopital's rule allows us to replace the limit problem
indeterminate form infinity over infinity
with another simpler problem to solve.
Second Version of l'Hopital theorem

Example 1

Find the limit \( \lim_{x\to \infty} \dfrac{\ln x}{x} \)
Solution to Example 1:
Since
\( \lim_{x\to \infty} \ln x = \infty\)
and
\( \lim_{x\to \infty} x = \infty\)
we have the indeterminate form
\( \lim_{x\to \infty} \dfrac{\ln x}{x} = \dfrac{\infty}{\infty} \)
The above L'Hopital's rule can be used to evaluate the given limit question as follows
\( \lim_{x\to \infty} \dfrac{\ln x}{x} = \lim_{x\to \infty} \dfrac{ (\ln x)' }{(x)'} \)
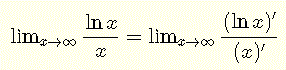
Evaluate the derivatives in the numerator and the denominator
\(= \lim_{x\to \infty} \dfrac{ 1/x }{1}\)
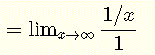
Evaluate the limits in the numerator and denominator
\( \lim_{x\to \infty} (1/x) = 0 \) and \( \lim_{x\to \infty} 1 = 1 \)
We now evaluate the given limit
\( \lim_{x\to \infty} \dfrac{\ln x}{x} = \lim_{x\to \infty} \dfrac{ 0 }{1} = 0 \)

Example 2

Find \( \lim_{x\to \infty} x e^{-x} \)
Solution to Example 2:
Note that
\( \lim_{x\to \infty} x = \infty \)
and
\( \lim_{x\to \infty} e^{-x} = 0 \)
This is the indeterminate form \( \infty \cdot 0 \). The idea is to convert it into to the indeterminate form \( \dfrac{\infty}{\infty} \) and use L'Hopital's theorem. Note that
\( \lim_{x\to \infty} x e^{-x} = \lim_{x\to \infty} \dfrac{ x}{ e^x} = \dfrac{ \infty }{ \infty }\)
We apply the above L'Hopital's theorem
\( = \lim_{x\to \infty} \dfrac{ (x)'}{ (e^x)'} = \lim_{x\to \infty} \dfrac{ 1 }{ e^x} = 0\)

Example 3

Find \( \lim_{x\to \infty} ( 1 + 1/x)^x \)

Solution to Example 3:
Note that \( \lim_{x\to \infty} (1 + 1/x) = 1 \) and the above limit is given by
\( \lim_{x\to \infty} ( 1 + 1/x)^x = 1^{\infty}\)
which is of the Indeterminate form \( 1^{\infty}\). If we let \( t = 1 / x \) the above limit may written as
\( \lim_{x\to \infty} ( 1 + 1/x)^x = \lim_{t\to 0} ( 1 + t)^{1/t} \) , note that as \( x\to \infty \) , \( t\to 0 \)
Let \( y = ( 1 + t)^{1/t} \) and find the limit of \( \ln y \) as t approaches 0
\( \ln y = \ln ( 1 + t)^{1/t} =(1 / t) \ln (1 + t) \)
The advantage of using \( \ln y \) is that
\( \lim_{t\to 0} \ln y = \lim_{t\to 0} \dfrac {\ln (1 + t)}{t} = \dfrac{0}{0} \)
and the limit has the indeterminate form 0 / 0 and the first L'Hopital's rule can be applied
\( \lim_{t\to 0} \ln y = \lim_{t\to 0} \dfrac {ln (1 + t)}{t} \)
\( = \lim_{t\to 0} \dfrac{(ln (1 + t))'}{(t)'} = \lim_{t\to 0} \dfrac{1/(1+t)}{1} = 1\)
Since the limit of ln y = 1 the limit of y is e 1 = e, hence
\( \lim_{x\to \infty} ( 1 + 1/x)^x = e \)

Example 4

Find the limit \( \lim_{x\to 0^+} ( 1 / x - 1 / \sin x )\)
Solution to Example 4:
Note that
\( \lim_{x\to 0^+} ( 1 / x ) = + \infty \)
and
\( \lim_{x\to 0^+} ( 1 / \sin x ) = + \infty \)
This limit has the indeterminate form \( \infty - \infty \) and has to be converted to another form by combining \( 1 / x - 1 / sin x \)
\( \lim_{x\to 0^+} ( 1 / x - 1 / \sin x ) = \lim_{x\to 0^+} \dfrac{\sin x - x}{x \sin x} = \dfrac{0}{0} \)
We now have the indeterminate form 0 / 0 and we can use the L'Hopital's theorem.
\( \lim_{x\to 0^+} \dfrac{\sin x - x}{x \sin x} = \lim_{x\to 0^+} \dfrac{(\sin x - x)'}{(x \sin x)'} = \lim_{x\to 0^+} \dfrac{\cos x - 1}{ \sin x + x \cos x} = \dfrac{0}{0} \)
We have again the indeterminate form 0 / 0 and use the L'Hopital's theorem one more time.
\( = \lim_{x\to 0^+} \dfrac{(\cos x - 1)'}{ (\sin x + x \cos x)'} \)
\( = \lim_{x\to 0^+} \dfrac{-\sin x}{ \cos x + \cos x - x \sin x } = \dfrac{0}{2} = 0\)

Example 5

Find the limit \( \lim_{x\to 0^+} x^x \)
Solution to Example 5:
We have the indeterminate form 00. Let y = x x and ln y = ln (x x) = x ln x. Let us now find the limit of ln y
\( \lim_{x\to 0^+} \ln y = \lim_{x\to 0^+} x \ln x = 0 \cdot \infty\)
The above limit has the indeterminate form \( 0 \cdot \infty\). We have convert it as follows
\( \lim_{x\to 0^+} x \ln x = \lim_{x\to 0^+} \dfrac{\ln x}{1/x} = \dfrac{\infty}{\infty} \)
It now has the indeterminate form \( \dfrac{\infty}{\infty} \) and we can use the L'Hopital's theorem
\( \lim_{x\to 0^+} \dfrac{\ln x}{1/x} = \lim_{x\to 0^+} \dfrac{(\ln x)'}{(1/x)'} \)
\( = \lim_{x\to 0^+} \dfrac{1/x}{-1/x^2} \)
\( = \lim_{x\to 0^+} - x = 0\)
The limit of ln y = 0 and the limit of y = xx is equal to
\( e^0 = 1 \)

Exercises

Find the limits
1. \( \lim_{x\to \infty} (\ln x)^{1/x} \)
2. \( \lim_{x\to \infty} (\ln x - \ln (1 + x)) \)
3. \( \lim_{x\to \infty} \dfrac{x}{e^x} \)
4. \( \lim_{x\to 0^+} x^{\sin x} \)

Solutions to Above Exercises

1. 1
2. 0
3. 0
4. 1

More Links on Limits

Calculus Tutorials and Problems
Limits of Absolute Value Functions Questions