Trouver les interceptions x et y, le sommet et l'axe de symétrie de la parabole avec l'équation \( y = - x^2 + 2 x + 3 \) ?
Quels sont les points d'intersection de la droite d'équation \( 2x + 3y = 7 \) et de la parabole d'équation \( y = - 2 x^2 + 2 x + 5\) ?
Trouvez les points d'intersection des deux paraboles avec l'équation \( y = -(x - 3)^2 + 2\) et \( y = x^2 - 4x + 1\).
Trouvez l'équation de la parabole \( y = 2 x^2 + b x + c\) qui passe par les points \( (-1,-5)\) et \( (2,10)\).
Quelle est l'équation de la parabole avec x interceptions a \( x = 2\) et \( x = -3\), et une y interceptions à \( y = 5\) ?
Trouver l'équation de la parabole \( y = a x^2 + b x + c \) qui passe par les points \( (0,3) \) , \( (1,-4)\) et \( (-1 , 4)\).
Trouver l'équation de la parabole, d'axe de symétrie vertical, qui est tangente à la droite \( y = 3 \) en \( x = -2 \) et dont la courbe passe par le point \( (0,5) \).
Pour quelle valeur de la pente \( m \) la droite d'équation \( y = m x - 3 \) est-elle tangente à la parabole d'équation \( y = 3 x^2 - x \) ?
Pour quelles valeurs du paramètre \( b \) la droite de l'équation \( y = 2 x + b \) coupe-t-elle la parabole de l'équation \( y = - x^2 - 2 x + 1\) en deux points ?
Trouvez l'équation \( y = a x^2 + x\) de la parabole tangente à la droite d'équation \( y = 3 x + 1\).
Déplacez le graphique de la parabole \( y = x^2 \) vers la gauche de 3 unités, puis reflètez le graphique résultant sur l'axe des x, puis déplacez-le vers le haut de 4 unités. Quelle est l’équation de la nouvelle parabole après ces transformations ?
Quelles transformations sont nécessaires pour transformer le graphe de la parabole \( y = x^2 \) en le graphe de la parabole \( y = - x^2 + 4 x + 6 \) ?
Écrivez l’équation de la parabole indiquée dans le graphique ci-dessous.
Solutions aux questions et problèmes ci-dessus
Les abscisses à l’origine sont l’intersection de la parabole avec l’axe des x, qui sont des points sur l’axe des x et donc leurs coordonnées y sont égales à 0. Par conséquent, nous devons résoudre l’équation :
\( 0 = -x^2 + 2x + 3 \)
Factoriser le côté droit de l'équation : \( -(x - 3)(x + 1) = 0\)
Les abscisses à l'origine sont : Résoudre pour x : \(x = 3\) y \(x = -1\) ,
Les ordonnées à l'origine sont l'intersection de la parabole avec l'axe y, qui est un point sur l'axe y et, par conséquent, ses coordonnées x sont égales à 0.
l'ordonnée à l'origine est :\( y = - (0)^2 + 2 (0) + 3 = 3 \),
Le sommet est trouvé en écrivant l'équation de la parabole sous la forme du sommet \(y = a(x - h)^2 + k \) en complétant le carré et en identifiant les coordonnées du sommet \( h \) et \( k \) .
Complétez le carré : \(y = - x^2 + 2 x + 3 = -( x^2 - 2 x - 3) = -( (x - 1)^2 - 1 - 3) = -(x - 1 )^2 + 4 \)
Sommet au point \( (1 , 4) \)
Vous pouvez vérifier tous les points ci-dessus trouvés à l’aide du graphique de \( y = - x^2 + 2 x + 3 \) ci-dessous.
Les points d'intersection sont des solutions des équations simultanées du système \( 2x + 3y = 7 \) et \( y = - 2 x^2 + 2 x + 5 \).
Puisque \( y = - 2 x^2 + 2 x + 5 \), remplacez \( - 2 x^2 + 2 x + 5 \) par y dans l'équation \( 2x + 3y = 7 \) de la manière suivante
\( 2x + 3(- 2x^2 + 2x + 5) = 7 \)
Écrivez l'équation quadratique obtenue ci-dessus sous forme standard
\( -6x^2 + 8x + 8 = 0 \)
Divisez tous les termes de l'équation par 2.
\( -3x^2 + 4x + 4 = 0 \)
Solution pour x
\( x = 2 , x = -2/3 \)
Remplacez x par les solutions précédentes dans \( 2x + 3y = 7 \) pour trouver y.
\( x = 2 , y = 1 \) et \( x = -2/3 , y = 25/9 \)
Les points d'intersection sont : \( (2 , 1) \) et \( (-2/3 , 25/9) \).
Vérifiez la réponse graphiquement ci-dessous.
Les points d'intersection des deux paraboles sont des solutions des équations simultanées
\( y = -(x - 3)^2 + 2 \) et \( y = x^2 - 4x + 1 \).
Éliminez \( y \) et dérivez l'équation à une inconnue
\( -(x - 3)^2 + 2 = x^2 - 4x + 1 \)
\( -2x^2 + 10x - 8 = 0 \)
\( -x^2 + 5x - 4 = 0 \)
Les solutions de l'équation quadratique ci-dessus sont :
\(x = 1 \) et \(x = 4 \)
Utilisez l'une des équations pour trouver y :
\(x = 1 \) dans l'équation \(y = -(x - 3)^2 + 2 \) pour obtenir \( y = -(1 - 3)^2 + 2 = -2 \)
\( x = 4 \) dans l'équation \( y = -(x - 3)^2 + 2 \) pour obtenir \( y = -(4 - 3)^2 + 2 = 1 \)
Points : \( (1 , -2) \) et \( (4 , 1) \)
Vérifiez la réponse graphiquement ci-dessous.
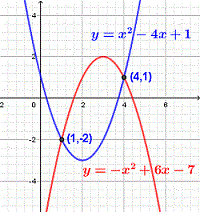
Les points \((-1,-5)\) et \((2,10) \) sont sur le graphique de la parabole \( y = 2 x^2 + b x + c\), donc.
\( -5 = 2 (-1)^2 + b (-1) + c\)
\( 10 = 2 (2)^2 + b (2) + c\)
Réécrivez le système ci-dessus en b et c sous forme standard.
\( -b + c = - 7\)
\( 2b + c = 2\)
Résolvez le système d'équations ci-dessus pour obtenir : \( c = - 4 \) et \( b = 3\)
L'équation de la parabole qui passe par les points \( (-1,-5)\) et \( (2,10)\) est : \( y = 2 x^2 + b x + c = 2 x^2 + 3x-4\)
Utilisez un traceur graphique pour vérifier votre réponse en traçant graphiquement \( y = 2 x^2 + 3 x - 4 \) et Vérifiez que le graphique passe par les points \( (-1,-5) \) et \((2,10)\).
L'équation d'une parabole avec des abscisses à l'origine en \( x = 2 \) et \( x = -3 \) peut être écrite comme le produit de deux facteurs dont les zéros sont les abscisses à l'origine comme suit :
\( y = a (x - 2)(x + 3) \)
Nous utilisons maintenant l'ordonnée à l'origine en (0, 5), qui est un point par lequel passe la parabole, pour écrire :
\( 5 = a (0 - 2)(0 + 3) \)
Résoudre pour \(a\)
\( a = - 5 / 6 \)
Équation : \( y = (-5/6)(x - 2)(x + 3)\)
Tracez le graphique \( y = (-5/6)(x - 2)(x + 3)\) et vérifiez que le graphique a une ordonnée à l'origine en \( x = 2 , x = -3 \) et un y - intercepter a \( y = 5\).
Les points \( (0,3), (1,-4) \) et \( (-1,4) \) se trouvent sur le graphique de la parabole \( y = a x^2 + b x + c \) et sont donc des solutions à l'équation de la parabole. On écrit donc le système de 3 équations comme suit :
Le point \( (0,3) \) donne l'équation : \( 3 = a (0)^2 + b (0) + c \quad (I) \)
Le point \( (1,-4) \) donne l'équation : \( - 4 = a (1)^2 + b (1) + c \quad (II) \)
Le point \( (-1,4) \) donne l'équation : \( 4 = a (-1)^2 + b (-1) + c \quad (III) \)
L'équation (I) donne :
\( c = 3 \)
Remplacez c par 3 dans les équations (II) et (III)
\(a + b = -7 \)
\( a - b = 1 \)
Résoudre le système en a et b
\( a = - 3 \) et \( b = - 4 \)
Équation : \( y = a x^2 + b x + c = -3 x^2 - 4x + 3 \)
Représentez graphiquement les graphiques de \( y = -3 x^2 - 4x + 3 \) et vérifiez que le graphique passe par les points \( (0,3), (1,-4) \) et \( (-1 ,4)\).
L'équation de la parabole, d'axe de symétrie vertical, a la forme \( y = a x^2 + b x + c \) ou sous forme de sommet \( y = a(x - h)^2 + k \) où le le sommet est au point \( (h , k)\) .
Dans ce cas il est tangent à une droite horizontale \( y = 3 \) en \( x = -2 \) ce qui signifie que son sommet est au point \( (h , k) = (-2 , 3) \). L’équation de cette parabole peut donc s’écrire :
\( y = a (x - h)^2 + k = a (x - (-2))^2 + 3 = a (x + 2)^2 + 3 \)
Son graphe passe par le point \( (0 , 5) \). C'est pourquoi
\( 5 = a (0 + 2)^2 + 3 = 4 a + 3 \)
Résolvez ce qui précède pour \( a \)
\( a = 1 / 2 \)
Équation : \( y = (1/2)(x + 2)^2 + 3 \)
Esquissez les graphiques de \( y = (1/2)(x + 2)^2 + 3 \) et vérifiez que le graphique est tangent à la ligne horizontale \( y = 3 \) en \( x = -2 \) et aussi le graphe passe par le point \( (0 , 5) \).
Une droite et une parabole sont tangentes si elles n'ont qu'un seul point d'intersection, qui est le point où elles se touchent.
Les points d'intersection sont trouvés en résolvant le système
\( y = m x - 3 \) y \( y = 3 x^2 - x \)
\( m x - 3 = 3 x^2 - x \)
Écrivez sous forme d’équation quadratique standard :
\( 3 x ^ 2 - x (1 + m) + 3 = 0 \)
Le discriminant de l’équation quadratique ci-dessus est donné par :
\( \Delta = (1 + m)^2 - 4(3)(3) \)
La droite est tangente à la parabole des graphiques des deux courbes ont un point d'intersection si :
\( \Delta = 0 \) (cas d'une solution d'une équation quadratique)
D'où l'équation :
\( (1 + m)^2 - 4(3)(3) = 0 \)
résoudre pour moi
\( (1 + m)^2 = 36 \)
Solutions : \( m = 5 \) et \( m = -7 \)
Utilisez un traceur de graphiques pour vérifier votre réponse en traçant les graphiques des droites : \( y = 5 x - 3 \) (m = 5 solution ), \( y = -7 x - 3 \) (m = 7 solution) et la parabole \( y = 3 x^2 - x\) et vérifiez que les deux droites sont tangentes au graphique de la parabole \( y = 3 x^2 - x\).
Les points d'intersection sont trouvés en résolvant le système
\( y = 2 x + b \) et \(y = - x^2 - 2x + 1 \)
\( 2x + b = - x^2 - 2x + 1 \)
Écrivez sous forme d’équation quadratique standard :
\( - x ^ 2 - 4x + 1 - b = 0 \)
Le discriminant de l'équation ci-dessus est donné par : \( \Delta = (-4)^2 - 4(-1)(1 - b) = 20 - 4b \)
Les graphes de \( y = 2 x + b \) et \( y = - x^2 - 2 x + 1 \) ont deux points d'intersection si \( \Delta \gt 0 \) (cas de deux solutions réelles d'une équation quadratique)
\( 20 - 4 b \gt 0 \)
Résoudre pour b
\( b \lt 5 \)
Utilisez un traceur de graphiques pour vérifier votre réponse en traçant des graphiques de \( y = - x^2 - 2 x + 1 \) et des lignes passant par les équations \( y = 2 x + b \) pour les valeurs de \( b \gt 5 \) , \( b \lt 5 \) et \( b = 5 \) pour voir combien de points d'intersection de la parabole et de la droite il y a pour chacune de ces valeurs de \( b \).
Les points d'intersection sont trouvés en résolvant le système
\( y = a x^2 + x \) y \( y = 3 x + 1 \)
\( 3 x + 1 = a x^2 + x \)
Écrivez sous forme d’équation quadratique standard :
\( a x^2 - 2 x - 1 = 0 \)
Discriminant : \( \Delta = (-2)^2 - 4(a)(-1) = 4 + 4 a \)
Les graphes sont tangents s'ils ont un point d'intersection (cas d'une solution d'une équation quadratique) si \( \Delta = 0 \). C'est pourquoi
\( 4 + 4 a = 0 \)
Résoudre pour \(a\)
\(a = -1 \)
Équation parabolique : \( y = - x^2 + x \)
Graphiquez \( y = - x^2 + x \) et \( y = 3 x + 1 \) pour vérifier la réponse ci-dessus.
Début : \( y = x^2 \)
Décalage de 3 unités vers la gauche : \( y = (x + 3)^2 \)
Réfléchissez à l'axe des x : \( y = - (x + 3)^2 \)
Décaler de 4 unités : \( y = -(x + 3)^2 + 4 \)
Étant donné : \( y = - x^2 + 4 x + 6 \)
Réécrivez sous forme de sommet en complétant le carré : \( y = - x^2 + 4 x + 6 = - (x - 2)^2 + 10\)
Début : \( y = x^2\)
Décaler de 2 unités vers la droite : \( y = (x - 2)^2\)
Réfléchissez à l'axe des x : \( y = -(x - 2)^2 \)
Augmentez de 10 unités : \( y = -(x - 2)^2 + 10\)
N'importe quel point identifié sur le graphique donné peut être utilisé pour trouver l'équation de la parabole. Cependant, utiliser les coordonnées à l’origine x et y et le sommet sont de meilleurs moyens de trouver l’équation de la parabole dont le graphique est présenté ci-dessous.
Deux méthodes sont présentées pour résoudre le problème :
méthode 1 :
Le graphique comporte deux abscisses à l'origine : (-5, 0) et (-1, 0)
Utilisez les deux abscisses à l’origine en (-5, 0) et (-1, 0) pour écrire l’équation de la parabole comme suit :
\( y = a (x + 1)(x + 5)\)
Utilisez l'ordonnée à l'origine en (0, -5) pour écrire
\( - 5 = a (0 + 1)(0 + 5) = 5 a\)
Résoudre pour \(a \)
\(a = -1\)
Écrivez l'équation de la parabole :
\( y = -(x + 1)(x + 5) = - x^2 - 6 x - 5\)
méthode 2 :
Utilisez le sommet à \( ( h , k) = (-3 , 4) \) pour écrire l'équation de la parabole sous forme de sommet comme suit :
\( y = a (x - h)^2 + k = a(x + 3)^2 + 4 \)
Utilisez l'ordonnée à l'origine (0, -5) pour trouver \(a\).
\( - 5 = a (0 + 3)^2 + 4 \)
Résolvez ce qui précède pour \(a\) : \( a = -1 \)
L'équation de la parabole est donnée par
\(y = -(x + 3)^2 + 4 = - x^2 -6 x - 5 \)
