Problems on area and perimeter of squares with detailed solutions.
Problems
Problem 1
When the sides of a square are each increased by 2 feet, its area increases by 44 ft². Find the original side length \( s \).
Problem 2
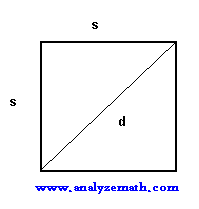
Find the area and perimeter of a square with a diagonal of 200 meters.
Problem 3
What happens to the area of a square if we double its side length?
Problem 4
A square garden of 400 m² is surrounded by a walkway of constant width \( x \). The total area of the walkway is 500 m². Find the width \( x \).

Detailed Solutions
Solution to Problem 1
Let \( s \) be the original side length.
Original area: \( A_1 = s^2 \)
New side length: \( s + 2 \)
New area: \( A_2 = (s + 2)^2 \)
Given: \( A_2 = A_1 + 44 \)
So: \( s^2 + 44 = (s + 2)^2 \)
Expand: \( s^2 + 44 = s^2 + 4s + 4 \)
Simplify: \( 44 = 4s + 4 \)
Solve: \( 4s = 40 \)
Thus: \( s = 10 \) feet
Check: Original area = \( 10^2 = 100 \) ft², New area = \( 12^2 = 144 \) ft², Difference = 44 ft² ✓
Solution to Problem 2
Using the diagonal formula: \( d = s\sqrt{2} \)
Given \( d = 200 \) m, so \( s\sqrt{2} = 200 \)
Thus: \( s = \frac{200}{\sqrt{2}} = 100\sqrt{2} \) m
Area: \( A = s^2 = (100\sqrt{2})^2 = 20000 \) m²
Perimeter: \( P = 4s = 4 \times 100\sqrt{2} = 400\sqrt{2} \) m
Solution to Problem 3
Let original side = \( s \), area = \( s^2 \)
New side = \( 2s \), new area = \( (2s)^2 = 4s^2 \)
Ratio: \( \frac{4s^2}{s^2} = 4 \)
Answer: The area becomes 4 times larger.
Solution to Problem 4
Garden area = 400 m², so side length = \( \sqrt{400} = 20 \) m
Total area (garden + walkway) = \( 400 + 500 = 900 \) m²
Let walkway width = \( x \)
Total side length = \( 20 + 2x \)
Equation: \( (20 + 2x)^2 = 900 \)
Take square root: \( 20 + 2x = 30 \) (positive root since length > 0)
Solve: \( 2x = 10 \)
Thus: \( x = 5 \) m
Check: Total side = 30 m, total area = 900 m², walkway area = 900 - 400 = 500 m² ✓

