Graphing Tangent Functions

A step by step tutorial on graphing and sketching tangent functions. The graph, domain, range and vertical asymptotes of these functions and other properties are examined.

Review

Some of the properties of the graph of f(x) = tan(x) are as follows:
1 - The domain of tan x is the set of all the real numbers except at x = ?/2 + n×? , where n is any integer number.
2 - The range of tanx is the set of all real numbers.
3 - The vertical asymptotes of the graph of tan x are located at x = ?/2 + n×?, where n is any integer.
4 - The period of tan x is equal to ?.

Example 1

Graph
f( x ) = tan(x)
Over one period.
Solution to Example 1
tan x is undefined for values of x equal to ?/2 and -?/2. However we need to understand the behavior of the graph of tan x as x approaches ?/2 and -?/2. Let us look at the values of tan x for x close to ?/2 such that x is smaller then ?/2.

x	?/2-0.5	?/2-0.1	?/2-0.01	?/2-0.001	?/2
tan x	1.8	10.0	100.0	1000.0	undefined

We note that as x approaches ?/2 from the left (by values smaller than ?/2) tan x increases indefinitely. We say that the graph of tan x has an asymptote at x = ?/2. It is represented by a vertical broken red line x = ?/2 in the graph below.
We now look at the values of tan x for x close to -?/2 such that x is larger then -?/2.

x	-?/2+0.5	-?/2+0.1	-?/2+0.01	-?/2+0.001	-?/2
tan x	-1.8	-10.0	-100.0	-1000.0	undefined

We note that as x approaches -?/2 from the right (by values larger than -?/2) tan x decreases indefinitely. The graph of tan x has an asymptote at x = -?/2. It is represented by a vertical broken red line x = -?/2 in the graph below.
tan x has an asymptotic behavior close to ?/2 and -?/2. Using the values of tan x above plus the following values:
tan 0 = 0, tan (?/4) = 1 and tan (-?/4) = -1,
we start by plotting the points (0,0) , (?/4,1) and (-?/4,-1) and the vertical asymptotes.
points and asymptotes of tan x

We then draw a smooth curve passing by the points calculated. Close to the vertical asymptotes, the graph either goes upward indefinitely (close to x = ?/2 vertical asymptote) and downward indefinitely (close to x = -?/2 vertical asymptote).
graph of tan x with asymptotes

We now summarize the graphing of tan x as follows:
Step 1: Make a table of values over one period.

x	-?/2	-?/4	-0	?/4	?/2
tan x	VA	-1.0	0.0	1.0	VA

where VA means vertical asymptote.
Step 2: Plot the points and the vertical asymptotes.
Step 3: Draw a curve passing through all points and rising or falling vertically along the vertical asymptotes.

Example 2

Graph function f given by
f( x ) = 2 tan(2 x - ?/4)
Over one period.

Solution to Example 2
Let t = 2 x - ?/4. Let us make a table over one period (-?/2 , ?/2) using the variable t.

t	-?/2	-?/4	-0	?/4	?/2
2 tan t	VA	-2.0	0.0	2.0	VA

We now use the relationship between x and t, t = 2 x - ? / 4, to find the values of x corresponding to the values of t used in the above table. Solve t = 2 x - ?/4 for x.
x = t / 2 + ? / 8
A row showing the x values may be added to the above table: These values of x have been found using x = t / 2 + ? / 8 found above and the values of t in the table.

t	-?/2	-?/4	-0	?/4	?/2
2 tan t	VA	-2.0	0.0	2.0	VA
x	-?/8	0	?/8	2 ?/8	3 ?/8

We now have the values of the function 2 tan t and the corresponding x values. We have enough information to graph the given function.

the graph of f( x ) = 2 tan(2 x - ?/4) , example 2

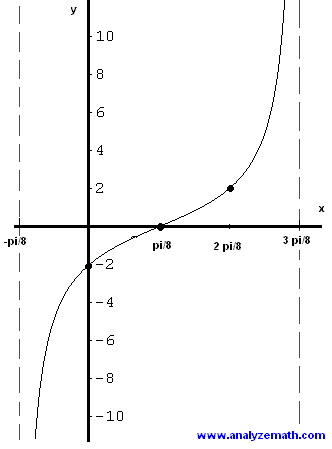
Example 3

Graph function f defined by
f( x ) = - tan(x + ?/2)
Over one period.
Solution to Example 3
Let t = x + ?/2. We first make a table using t over one period.

t	-?/2	-?/4	-0	?/4	?/2
- tan t	VA	1.0	0.0	-1.0	VA

Solve t = x + ?/2 for x.
x = t - ? / 2
A row showing the x values is added to the above table.

t	-?/2	-?/4	-0	?/4	?/2
- tan t	VA	1.0	0.0	-1.0	VA
x	-?	-3?/4	-?/2	- ?/4	0

We now have the values of the function - tan t and the corresponding x values.
the graph of f( x ) = - tan(x + ?/2) , example 3

Graphing Tangent Functions

Review

Example 1

Example 2

Example 3

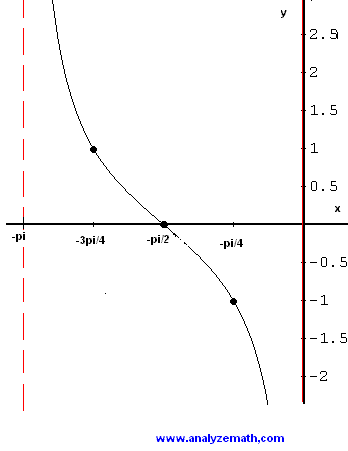
More References and Links to Graphing