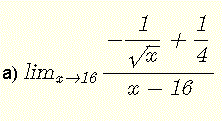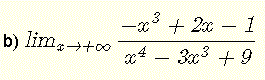Un ensemble de questions analyse 1 avec leurs solutions détaillées pour s'entraîner aux tests, examens, examens de placement, ... et acquérir une compréhension approfondie des sujets suivants :
Fonctions
Limites
Continuité
Dérivés
Applications de dérivés
Les questions ont été conçues pour couvrir les sujets les plus importants d'analyse 1 et leurs solutions détaillées incluent des liens vers plus de pratique dans ces sujets.
Question 1
Trouver le domaine de fonction
Question 2
trouver l'image de la fonction
\( \)\( \)\( \)\( \)\( \)
Question 3
Trouver l'inverse de la fonction \( f(x) = ln (2x - 3) + 2 \).
Question 4
Évaluez chacune des limites suivantes
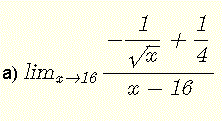
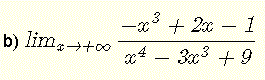
Question 5
a) Représenter \( y = e^{x-1} \) et \( y = x \) dans le même système de coordonnées puis montrer que les deux graphes sont tangents au point \( (1,1) \) et que \( e^{x-1} \ge x \)
b) Utilisez le résultat obtenu en a) pour déterminer la concavité de la fonction \( f(x) = \dfrac{x^3}{6} - e^{x-1} \) et les points d'inflexion s'il y en a.
Question 6
Trouvez la dérivée des fonctions suivantes et ne simplifiez pas la réponse finale.
Question 7
Trouver l'équation de la tangente à la courbe d'équation \( \sin(y^2) = x^2 \) au point \( ( 0,\sqrt{\pi}) \).
Question 8
Trouver les constantes \( a \) et \( b \) pour que la fonction \( f \) soit continue sur \( (-\infty , +\infty ) \)
\( f(x) = \left\{
\begin{array}{ll}
2x - 1 & x\le 1 \\
a x^3 + b & 1 \lt x \lt 2 \\
x + 2 b & x\ge 2 \\
\end{array}
\right. \)
Question 9
Trouvez l'équation de la tangente à la courbe d'équation \( y = x + \sin(x) \) à \( x = 0 \).
Question 10
Utilisez la définition de la dérivée comme limite pour trouver la dérivée \( f' \) où \( f(x) = \sqrt{x+2} \).
Question 11
Déterminez sur quel(s) intervalle(s) est la fonction \( f(x) = e^x(x^2-5x+8)+\dfrac{x^4}{12}-\dfrac{x^3}{6 } \) concave et convexe et tout point d'inflexion.
Question 12
Utilisez la méthode de Newton avec l'approximation initiale \( x_1 = 2 \) pour trouver une deuxième approximation de la solution de l'équation \( e^x = x^3 \).
Question 13
Trouver le maximum et le minimum absolus de la fonction \( f(x) = x^4 - x^3 \) sur l'intervalle \( [0,5] \).
Question 14
Si les dimensions \( L \),\( W \) et \( H\) d'une boîte rectangulaire changent aux taux \( \dfrac{dL}{dt} = 0,1 \; cm/sec \), \ ( \dfrac{dW}{dt} = - 0,2 \; cm/sec\) et \( \dfrac{dH}{dt} = 0,3 \; cm/sec\), à quelle vitesse est le volume de la boîte
changeant quand \( L = 20 \; cm \), \( W = 8 \; cm \) et \( H = 5 \; cm \) ?
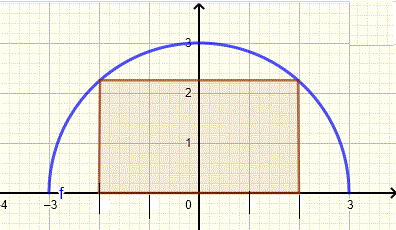
Question 15
Quelles sont les dimensions du rectangle d'aire la plus grande qui puisse s'inscrire dans un demi-cercle de rayon 3 ?
Solutions détaillées aux questions ci-dessus
Solution à la question 1
Pour que la fonction \( f \) prenne des valeurs réelles, l'expression sous le radical au numérateur doit être non négative, et l'expression sous le radical au dénominateur doit être positive ; d'où les inégalités à résoudre
\( x - 1 \ge 0 \) et \( 4 - x^2 \gt 0 \)
Les ensembles de solutions pour les première et deuxième inégalités sont respectivement
\( x \ge 1 \) et \( -2 \lt x \lt 2 \)
Les deux inégalités doivent être satisfaites simultanément, donc le domaine de la fonction donnée est l'intersection des ensembles \( x \ ge 1 \) et \( -2 \lt x \lt 2 \) qui est donnée par
\( 1 \le x \lt 2 \)
Solution à la question 2
Selon les propriétés des fonctions inverses, une façon de trouver les l'image de la fonction donnée consiste à trouver le domaine de son inverse.
Prouvons d'abord que \( f \) est une une à une fonction puis trouvons sa inverse. Pour prouver que \( f \) est une fonction un à un et donc inversible, nous utilisons la contraposée de la fonction un à un et commençons par
\( f(a) = f(b) \) et prouver que \( a = b \). Ainsi
\( \dfrac{a - 1}{2-3 a} = \dfrac{b - 1}{2-3 b} \)
Croix multiplier
\( (a - 1)(2-3 b) = (2 - 3 a)(b - 1) \)
Développer
\( 2a - 2 - 3 a b + 3 b = 2 b - 2 - 3 ab + 3 a\)
Regrouper les termes similaires
\( 2 a = 2 b \)
résoudre pour a
\( a = b\)
ce qui prouve que la fonction \( f \) est une fonction un à un et a donc a une inverse
L'inverse de \( f \) peut être calculé à partir de l'équation
\( y = \dfrac{x - 1}{2-3x} \)
Croisez multiplier l'équation ci-dessus
\( 2 y - 3 x y = x - 1 \)
et résoudre pour \( x \)
\( x = \dfrac{2 y + 1}{3y + 1} \)
Échangez \( x \) et \( y \) dans l'équation ci-dessus pour obtenir l'inverse \( f^{-1} \)
\( f^{-1}(x) = y = \dfrac{2 x + 1 }{3x + 1} \).
La domaine de \( f^{-1} \) est l'ensemble de tous les nombres réels sauf \( -\dfrac{1}{3} \). Par conséquent, l'image de \( f \) est l'ensemble de tous les nombres réels sauf \( -\dfrac{1}{3} \) qui peut être écrit sous forme d'intervalle comme
\( (-\infty , - \dfrac{1}{3}) \cup (- \dfrac{1}{3} , +\infty) \)
Solution à la question 3
Écrivez la fonction sous la forme d'une équation comme suit
\( y = ln (2x - 3) + 2 \)
Résolvez ce qui précède pour x
\( y - 2 = ln (2x - 3) \)
\( 2x - 3 = e^{y - 2} \)
\( 2 x = e^{y - 2} + 3 \)
\( x = \dfrac{1}{2} (e^{y - 2} + 3) \)
Échangez \( x \) et \( y \)
\( y = \dfrac{1}{2} (e^{x - 2} + 3) \)
L'inverse de \( f \) est donné par
\( f^{-1}(x) = \dfrac{1}{2} (e^{x - 2} + 3) \)
Solution à la question 4
a)
La limite est de la forme indéterminée \( \dfrac{0}{0} \).
Multipliez le numérateur et le dénominateur par le conjugué du numérateur \( -\dfrac{1}{\sqrt x} - \dfrac{1}{4} \)
b)
La limite est de la forme indéterminée \( \dfrac{\infty}{\infty} \).
Divisez tous les termes du numérateur et tous les termes du dénominateur par avec le terme avec la puissance la plus élevée qui dans \( x^4 \)
\( \lim_{x\to +\infty} \dfrac{-x^3+2x-1}{x^4 - 3 x^3 + 9 } = \lim_{x\to +\infty} \dfrac{ \dfrac{-x^3}{x^4}+\dfrac{2x}{x^4}-\dfrac{1}{x^4}}{\dfrac{x^4}{x^4} - \dfrac{3x^3}{x^4} + \dfrac{9}{x^4} }\).
Simplifier les termes rationnels
\( = \lim_{x\to +\infty} \dfrac{\dfrac{-1}{x}+\dfrac{2}{x^3}-\dfrac{1}{x^4}}{1 - \dfrac{3}{x} + \dfrac{9}{x^4} } = \dfrac{0+0-0}{1 - 0 + 0 } = \dfrac{0}{1} = 0\)
c)
La limite est de la forme indéterminée \( \infty \cdot 0 \).
Soit \( t = \dfrac{3}{x} \) et réécrivons la limite en termes de t.
\( \lim_{x\to +\infty} x \sin(\dfrac{3}{x}) = \lim_{t\to 0} 3 \dfrac {\sin(t)}{t} \).
En utilisant le résultat bien connu \( \lim_{t\to 0} \dfrac {\sin(t)}{t} = 1 \), la limite est évaluée à
\( = 3 \times 1 = 3\)
d)
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \dfrac{0}{0}\), forme indéterminée
Utiliser la Règle de L'Hospital à la forme indéterminée, on peut écrire
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \lim_{x\to 0} \dfrac{ d (\sin(x)+x) / dx }{ d(2x^2+x)/dx} = \lim_{x\to 0} \dfrac{ cos(x)+ 1 }{ 4x+1} = \dfrac{ cos(0)+ 1 } { 4\times 0+1} = 2\)
e)
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} \).
Il est bien connu que la plage de \( \sin(x) \) est donnée par
\( -1 \le \sin(x) \le 1 \)
Ajouter 1 à tous les termes de l'inégalité pour obtenir l'inégalité suivante
\( -1 + 1 \le \sin(x) + 1 \le 1 + 1 \)
\( 0 \le \sin(x) + 1 \le 2 \)
Diviser tous les termes de l'inégalité ci-dessus par positif \( x \)
\( \dfrac{0}{x} \le \dfrac{\sin(x) + 1}{x} \le \dfrac{2}{x} \)
On a \( \lim_{x\to +\infty} \dfrac{0}{x} = 0 \) et \( \lim_{x\to +\infty} \dfrac{2}{x} = 0 \)
En utilisant le théorème de compression (ou sandwich) , nous pouvons évaluer la limite donnée comme suit
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} = 0 \)
Solution à la question 5
un)
Le graphique de \( y = e^{x-1} \) et \( y = x \) est présenté ci-dessous. La dérivée de \( y = e^{x-1} \) est égale à \( y ' = e^{x-1} \) et la pente \( m \) de la tangente en \( x = 1 \) est la valeur de la dérivée en \( x = 1\). Ainsi
\( m = e^{1-1}= 1 \)
L'équation de la tangente au point \( (1,1) \) est donnée par
\( y - 1 = 1 \times (x - 1) \)
Ce qui simplifie à
\( y = x \)
Ainsi les graphes de \( y = e^{x-1} \) et \( y = x \) sont tangents au point \( (1,1) \) et on peut donc affirmer graphiquement que \( e^ {x-1} \ge x \).
b)
Les dérivées première et seconde de \( f \) sont données par
\( f'(x) = \dfrac{x^2}{2}-e^{x-1} \)
\( f''(x) = x-e^{x-1} \)
Un point d'inflexion se produit à une valeur de \( x \) où \( f''(x ) \) changer de signe. Nous avons vu dans la partie a) que \( e^{x-1} \ge x \) qui peut s'écrire
\( x-e^{x-1} \le 0 \)
et donc \( f''(x) \) est négatif et a un zéro en \( x = 1 \). Donc le graphe de \( f(x) \) est concave vers le bas et n'a pas de point d'inflexion car \( f''(x) \) ne change pas de signe.
Solution à la question 6
a) La règle des dérivées donne : \( f'(x) = e^{x-1 } + \dfrac{3}{3x-1} + 2 \cos(2x+1) \)
b) Règle du produit des dérivées : \( g'(x) = 4(2x-1)(\tan(x)-1) + (2x-1)^2(\sec^2(x)) \)
c) règle du quotient des dérivées : \( h'(x) = \dfrac{ (1 + \sin(x))(x^2-2x+1) - (x - \cos(x))(2x-2 ) }{(x^2-2x+1)^2} \)
d) Soit \( u = \sqrt{x^3 - \dfrac{1}{x} + 2} \) , écrivez la fonction \(m \) comme \(m = \sin u \) puis utilisez le règle de chaîne des dérivées
e)
Réécrivez \( 3^{ 2x+3} \) et \( \log_3(2x-1) \) comme
\( 3^{2x+3} = e^{(2x+3) \ln 3}\) , changement de base des exponentielles
\( \log_3(2x-1) = \dfrac{ \ln(2x-1)}{ \ln 3}\) , changement de base des logarithmes
Remplacez et réécrivez \( n(x) \) comme
\( n(x) = 3^{ 2x+3} + \log_3(2x-1) = e^{(2x+3) \ln 3} + \dfrac{ \ln(2x-1)}{ \ln 3} \)
On calcule maintenant la dérivée
\( n'(x) = ( 2 \ln 3 ) e^{(2x+3) \ln 3} + \dfrac{1}{ \ln 3} \dfrac{2}{2x-1} = ( 2 \ln 3 ) 3^{2x+3} + \dfrac{2}{\ln 3(2x-1)} \)
Solution à la question 7
Nous différencions d'abord l'équation donnée implicitement
\( 2 y \dfrac{d y}{d x} cos(y^2) = 2 x \)
\( \dfrac{d y}{d x} = \dfrac{ x}{ y cos(y^2)} \)
La pente \( m \) de la tangente est donnée par la valeur de \( \dfrac{d y}{d x} \) au point \( ( 0,\sqrt{\pi}) \).
\( m = \dfrac{(0)}{\sqrt{\pi} cos((\sqrt{{\pi}})^2)} = 0 \)
L'équation, sous forme de pente ponctuelle, de la tangente à la courbe au point \( ( 0,\sqrt{\pi}) \) est donnée par
\( y - \sqrt{\pi} = 0(x - 0) \)
C'est une ligne horizontale donnée par
\( y = \sqrt{\pi} \)
Solution à la question 8
\( f(x) \) est continue sur les intervalles \( (-\infty , 1) \) , \( (1,2) \) et \( (2 , +\infty) \). Il faut trouver \( a \) et \( b \) pour qu'il soit aussi continu en \( x = 1 \) et \( x = 2 \) et donc continu sur \( (-\infty , +\infty ) \).
\( f(1) = 1 \)
\( \lim_{x\to 1^-} f(x) = 1 \)
\( \lim_{x\to 1^+} f(x) = a(1)^3+b = a + b \)
Les limites de gauche et de droite de \( 1 \) doivent être égales
\( a + b = 1 \) (équation 1)
\( f(2) = 2 + 2 b \)
\( \lim_{x\to 2^-} f(x) = a(2)^3 + b = 8 a + b \)
\( \lim_{x\to 2^+} f(x) = 2 + 2 b \)
Les limites de gauche et de droite de \( 2 \) doivent être égales
\( 8 a + b = 2 + 2 b \) (équation 2)
Résoudre les équations (1) et (2) simultanément pour trouver
\( a = \dfrac{1}{3} \) et \( b = \dfrac{2}{3} \)
Solution à la question 9
Trouvez la dérivée de \( y \).
\( y' = 1 + \cos(x) \)
La pente \( m \) de la tangente en \( x = 0 \) est égale à la valeur de \( y' \) en \( x = 0 \). Ainsi
\( m = 1 + \cos(0) = 2 \)
La coordonnée y du point de tangence \( P \) est donnée par la valeur de \( y \) à \( x = 0 \). Ainsi
\( P(0 , 0 + \sin(0)) = P(0,0) \)
L'équation de la ligne tangente sous forme de pente ponctuelle est donnée par
\( y - 0 = 2(x - 0) \)
et sous forme d'intersection de pente
\( y = 2 x \)
Solution à la question 10 La définition de la dérivée \( f' \) de la fonction \( f \) est donnée par la limite
\( f'(x) = \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \)
Remplacez \( f(x) \) par \( \sqrt{x+2} \) dans la définition ci-dessus pour obtenir
\( f'(x) = \lim_{h\to 0} \dfrac{\sqrt{x + h +2}- \sqrt{x+2} }{h} \)
La limite ci-dessus est de la forme indéterminée \( \dfrac{0}{0} \). Multiplier le numérateur et le dénominateur par le conjugué du numérateur
\( f'(x) = \lim_{h\to 0} \dfrac{ (\sqrt{x + h +2}- \sqrt{x+2} ) (\sqrt{x + h +2} + \ sqrt{x+2} ) }{h(\sqrt{x + h +2} + \sqrt{x+2} )} \)
Développer le numérateur et simplifier
\( f'(x) = \lim_{h\to 0} \dfrac{ (x + h + 2)- (x + 2) ) }{h(\sqrt{x + h +2} + \sqrt{ x+2} )} = \lim_{h\to 0} \dfrac{ h }{h(\sqrt{x + h +2} + \sqrt{x+2} )}\)
Diviser le numérateur et le dénominateur par \( h \) (ou annuler \( h \))
\( f'(x) = \lim_{h\to 0} \dfrac{ 1 }{\sqrt{x + h +2} + \sqrt{x+2} }\)
Évaluer la limite et donc la dérivée
\( f'(x) = \dfrac{ 1 }{ \sqrt{x + 0 + 2} + \sqrt{x + 2} } = \dfrac{ 1 }{2 \sqrt{x + 2} }\)
Solution à la question 11
Trouver les dérivées premières et secondes
\( f'(x) = e^x (x^2-5x+8) + e^x (2 x -5) +\dfrac{x^3}{3}-\dfrac{x^2}{ 2} = e^x (x^2-3x+3)+\dfrac{x^3}{3}-\dfrac{x^2}{2} \)
\( f''(x) = e^x(x^2-3x+3)+e^x(2x-3) + x^2-x = e^x(x^2-x)+x^ 2-x = x (x - 1) e^x \)
\( f'' \) a deux zéros : \( x = 0 \) et \( x = 1\) et \( e^x \) est toujours positif. Donc la table des signes de \( f'' \) a trois intervalles
1) \( (-\infty , 0 ) \) , valeur de test \( x = -1 \) , \( f''(-1) = 2/e \) , d'où \( f''(x) \) est positif sur l'intervalle \( (-\infty , 0 ) \).
2) \( (0 , 1 ) \) , valeur de test \( x = 1/2 \) , \( f''(1/2) = -\dfrac{\sqrt 2}{4} \) , donc \( f''(x) \) est négatif sur l'intervalle \( (0 , 1 ) \).
3) \( (1 , +\infty ) \) , la valeur de test \( x = 2 \) , \( f''(2) = 2e^2 \) , \( f''(x) \) est positif sur l'intervalle \( (1 , +\infty ) \).
\( f'' \) est concave sur les intervalles \( (-\infty , 0 ) \) et \( (1 , +\infty ) \) , et convex sur l'intervalle \( (0 , 1 ) \).
\( f'' \) change de signe en \( x = 0 \) et \( x = 1 \) et a donc des points d'inflexion en \( x = 0 \) et \( x = 1 \).
Solution à la question 12
La méthode de Newton est basée sur l'algorithme suivant : connaître une approximation \( x_n \) de la solution d'un équation \( f(x) = 0 \), la prochaine approximation \( x_{n+1}\) de l'équation est donnée par
\( x_{n+1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \).
La solution de l'équation donnée \( e^x = x^3 \) est égale à la solution de l'équation \( f(x) = e^x - x^3 = 0 \)
\( f'(x) = e^x - 3x^2 \)
Nous connaissons une première approximation \( x_1 = 2 \); en utilisant l'algorithme de Newton, nous approximons \(x_2\) par
\( x_{2} = x_1 - \dfrac{f(x_1)}{f'(x_1)} = 2 - \dfrac{e^2 - 2^3}{e^2 - 3 \times 2^2} \approx 1.87 \) (arrondi à deux décimales)
Une approximation \(x_3\) peut être obtenue en utilisant \(x_2 \) trouvé ci-dessus et ainsi de suite.
Solution à la question 13
Trouvez la dérivée première et factorisez-la.
\( f'(x) = 4 x^3 - 3 x^2 = x^2(4x - 3)\)
\( f'(x) \) a deux zéros à \( x = 0 \) et \( x = 3/4 \) et les deux sont dans l'intervalle \( [0,5] \). Les zéros de \( f'(x) \) sont appelés points critiques.
Nous évaluons maintenant la fonction aux extrémités de l'intervalle donné et les zéros de \( f'(x) \).
\( f(0) = 0 \)
\( f(5) = 5^4 - 5^3 = 500 \)
\( f(3/4) = (3/4)^4 - (3/4)^3 = -\dfrac{27}{256} \)
En comparant ces valeurs, \( f(x) \) a un maximum absolu égal à \(500 \) au point final \( x = 5 \) et un minimum absolu égal à \( -\dfrac{27}{256} \) au point critique \( x = 3/4 \)
Plus de questions sur minimum et maximum absolus d'une fonction inclus.
Solution à la question 14
Le volume \( V \) d'une boîte rectangulaire de dimensions \( L \),\( W \) et \( H\) est donné par
\( V = L(t) W(t) H(t) \)
où \( L(t)\) , \( W(t) \) et \( H(t) \) sont des fonctions du temps \( t \).
Étant donné que les dimensions de la boîte changent avec le temps, le volume de la boîte change également avec le temps au taux de changement de \( V\) est donnée par la dérivée première \( \dfrac{dV}{dt} \).
\( \dfrac{dV}{dt} = W(t) H(t) \dfrac{d L}{dt } + L(t) H(t) \dfrac{d W}{dt } + L(t ) W(t) \dfrac{d H}{dt } \)
Remplacer les grandeurs connues par leurs valeurs numériques
\( \dfrac{dV}{dt} = 8 \times 5 \times 0,1 + 20 \times 5 \times (-0,2) + 20 \times 8 \times 0,3 = 32 \; cm^3 / sec \)
Solution à la question 15 Équation d'un cercle de rayon \( 3 \) et de centre à \( (0 , 0) \)donné par
\( x^2 + y^2 = 3^2 \)
Résolvez l'équation ci-dessus pour y
\(y^2 = 9 - x^2\)
\( y = \pm \sqrt{9 - x^2} \)
L'équation du demi-cercle supérieur est
\( y = \sqrt(9-x^2) \)
Un point sur le demi-cercle de coordonnée x \( x \) a une coordonnée y égale à \(\sqrt{9 - x^2} \) (voir graphique ci-dessous)
Le rectangle a une longueur \( L = 2x \) et une largeur (ou hauteur) \( W = \sqrt(9-x^2) \). L'aire \( A \) du rectangle est donnée par
\( A(x) = L \times W = 2 x \sqrt(9-x^2) \) , \( 0 \le x \le 3 \)
Trouver la dérivée première de \( A \)
\( \dfrac{d A}{dx} = 2\sqrt{9-x^2} + (2x) (\dfrac{1}{2}) (-2x) (9-x^2)^{- 1/2} =\dfrac{2\left(-2x^2+9\right)}{\sqrt{9-x^2}} \)
Les zéros de \( \dfrac{d A}{dx} \) sont donnés par les zéros du numérateur de \( \dfrac{d A}{dx} \)
\( -2x^2+9 = 0 \)
Donne deux zéros : \( x = \sqrt{4.5} \) et \( x = - \sqrt{4.5} \)
On considère le zéro à \( x = \sqrt{4.5} \) puisqu'il est dans l'intervalle \( [0 , 3 ] \)
Nous évaluons maintenant l'aire \( A(x) \) aux extrémités \( x = 0 \) et \( x = 3 \) et au point critique \( x = \sqrt{4.5} \).
\( A(0) = 0 \)
\( A(3) = 0 \)
\( A(\sqrt{4.5}) = 9 \)
L'aire A est maximale est pour \( x = \sqrt{4.5} \)
Les dimensions sont :
\( L = 2 x = 2 \sqrt{4,5} \approx 4,24 \)
\( W = \sqrt(9-x^2) = \sqrt(9-\sqrt{4.5}^2) \approx 2.12 \)
Plus de problèmes d'optimisation inclus.
\( \)\( \)\( \)\( \)\( \)
