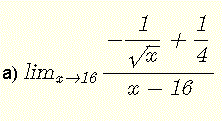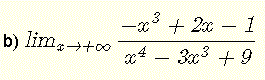Eine Reihe von Fragen zur Analysis 1 mit ihren detaillierten Lösungen zum Üben für Tests, Prüfungen, Einstufungsprüfungen usw. und zum Erwerb tiefer Kenntnisse zu den folgenden Themen:
Funktionen
Grenzwerte
Kontinuität
Derivate
Anwendungen von Derivaten
Die Fragen wurden so konzipiert, dass sie die wichtigsten Themen in Kalkül 1 abdecken, und ihre detaillierten Lösungen enthalten Links zu weiteren Übungen zu diesen Themen.
Frage 1
Finden die Domäne der Funktion
Frage 2
Finden Sie den Bereich der Funktion
\( \)\( \)\( \)\( \)\( \)
Frage 3
Finden Sie die Umkehrung der Funktion \( f(x) = ln (2x - 3) + 2 \).
Frage 4
Bewerten Sie jeden der folgenden Grenzwerte
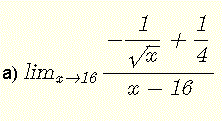
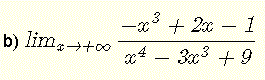
Frage 5
a) Zeichnen Sie \( y = e^{x-1} \) und \( y = x \) im gleichen Koordinatensystem und zeigen Sie dann, dass die beiden Graphen im Punkt \( (1,1) \) und dass \( e^{x-1} \ge x \)
b) Verwenden Sie das in Teil a) erhaltene Ergebnis, um die Konkavität der Funktion \( f(x) = \dfrac{x^3}{6} - e^{x-1} \) und gegebenenfalls Wendepunkte zu bestimmen.
Frage 6
Finden Sie die Ableitung der folgenden Funktionen und vereinfachen Sie die endgültige Antwort nicht.
Frage 7
Finden Sie die Gleichung der Tangente an die Kurve mit der Gleichung \( \sin(y^2) = x^2 \) am Punkt \( ( 0,\sqrt{\pi}) \).
Frage 8
Finden Sie die Konstanten \( a \) und \( b \), sodass die Funktion \( f \) stetig auf \( (-\infty , +\infty ) \) ist.
\( f(x) = \left\{
\begin{array}{ll}
2x - 1 & x\le 1 \\
a x^3 + b & 1 \lt x \lt 2 \\
x + 2 b & x\ge 2 \\
\end{array}
\right. \)
Frage 9
Finden Sie die Gleichung der Tangente an die Kurve mit der Gleichung \( y = x + \sin(x) \) bei \( x = 0 \).
Frage 10
Verwenden Sie die Definition der Ableitung als Grenzwert, um die Ableitung \( f' \) zu finden, wobei \( f(x) = \sqrt{x+2} \).
Frage 11
Bestimmen Sie, in welchen Intervallen die Funktion \( f(x) = e^x(x^2-5x+8)+\dfrac{x^4}{12}-\dfrac{x^3}{6} \) konkav nach oben und konkav nach unten und jeder Wendepunkt.
Frage 12
Verwenden Sie die Newton-Methode mit anfänglicher Näherung \( x_1 = 2 \), um eine zweite Näherung für die Lösung der Gleichung \( e^x = x^3 \) zu finden.
Frage 13
Finden Sie das absolute Maximum und Minimum der Funktion \( f(x) = x^4 - x^3 \) im Intervall \( [0,5] \).
Frage 14
Wenn sich die Abmessungen \( L \),\( W \) und \( H\) eines rechteckigen Kastens mit der Geschwindigkeit \( \dfrac{dL}{dt} = 0,1 \; cm/sec \) ändern, \( \dfrac{dW}{dt} = - 0,2 \; cm/sec\) und \( \dfrac{dH}{dt} = 0,3 \; cm/sec\), bei welcher Geschwindigkeit ist das Volumen der Box
ändert sich, wenn \( L = 20 \; cm \), \( W = 8 \; cm \) und \( H = 5 \; cm \)?
Frage 15
Welche Abmessungen hat das Rechteck mit der größten Fläche, das in einen Halbkreis mit Radius 3 eingeschrieben werden kann?
Detaillierte Lösungen zu den oben genannten Fragen
Lösung zu Frage 1
Damit die Funktion \( f \) reale Werte annimmt, darf der Ausdruck unter der Wurzel im Zähler nicht negativ und der Ausdruck unter der Wurzel im Nenner positiv sein; daher die zu lösenden Ungleichungen
\( x - 1 \ge 0 \) und \( 4 - x^2 \gt 0 \)
Die Lösungsmengen für die erste und zweite Ungleichung sind jeweils
\( x \ge 1 \) und \( -2 \lt x \lt 2 \)
Beide Ungleichungen müssen gleichzeitig erfüllt sein, daher ist der Domänen der gegebenen Funktion der Schnittpunkt der Mengen \( x \ ge 1 \) und \( -2 \lt x \lt 2 \), was gegeben ist durch
\( 1 \le x \lt 2 \)
Lösung zu Frage 2
Gemäß den Eigenschaften von Umkehrfunktionen gibt es eine Möglichkeit, die der angegebenen Funktion besteht darin, den Definitionsbereich ihrer Umkehrung zu ermitteln.
Lassen Sie uns zunächst beweisen, dass \( f \) eine Eins-zu-eins-Funktion ist, und dann ihre invers. Um zu beweisen, dass \( f \) eine Eins-zu-Eins-Funktion und daher invertierbar ist, verwenden wir das Kontrapositiv der Eins-zu-Eins-Funktion und beginnen mit
\( f(a) = f(b) \) und beweisen Sie, dass \( a = b \). Somit
\( \dfrac{a - 1}{2-3 a} = \dfrac{b - 1}{2-3 b} \)
Kreuzmultiplizieren
\( (a - 1)(2-3 b) = (2 - 3 a)(b - 1) \)
Expandieren
\( 2a - 2 - 3 a b + 3 b = 2 b - 2 - 3 ab + 3 a \)
Gruppenähnliche Begriffe
\( 2 a = 2 b \)
Lösen Sie nach a
\( a = b\)
was beweist, dass die Funktion \( f \) eine Eins-zu-Eins-Funktion ist und daher eine Umkehrung hat
Die Umkehrung von \( f \) kann ausgehend von der Gleichung berechnet werden
\( y = \dfrac{x - 1}{2-3x} \)
Kreuzmultiplizieren Sie die obige Gleichung
\( 2 y - 3 x y = x - 1 \)
und löse nach \( x \)
\( x = \dfrac{2 y + 1}{3y + 1} \)
Vertauschen Sie \( x \) und \( y \) in der obigen Gleichung, um die Umkehrung \( f^{-1} \) zu erhalten.
\( f^{-1}(x) = y = \dfrac{2 x + 1 }{3x + 1} \).
Der Domian von \( f^{-1} \) ist die Menge aller reellen Zahlen außer \( -\dfrac{1}{3} \). Daher ist der Bereich von \( f \) die Menge aller reellen Zahlen außer \( -\dfrac{1}{3} \), die in Intervallform als geschrieben werden können
\( (-\infty , - \dfrac{1}{3}) \cup (- \dfrac{1}{3} , +\infty) \)
Lösung zu Frage 3
Schreiben Sie die Funktion wie folgt als Gleichung
\( y = ln (2x - 3) + 2 \)
Lösen Sie das Obige nach x auf
\( y - 2 = ln (2x - 3) \)
\( 2x - 3 = e^{y - 2} \)
\( 2 x = e^{y - 2} + 3 \)
\( x = \dfrac{1}{2} (e^{y - 2} + 3) \)
Vertausche \( x \) und \( y \)
\( y = \dfrac{1}{2} (e^{x - 2} + 3) \)
Die Umkehrung von \( f \) ist gegeben durch
\( f^{-1}(x) = \dfrac{1}{2} (e^{x - 2} + 3) \)
Lösung zu Frage 4
a)
Der Grenzwert hat die unbestimmte Form \( \dfrac{0}{0} \).
Multiplizieren Sie Zähler und Nenner mit dem Konjugat des Zählers \( -\dfrac{1}{\sqrt x} - \dfrac{1}{4} \)
b)
Der Grenzwert hat die unbestimmte Form \( \dfrac{\infty}{\infty} \).
Dividiere alle Terme im Zähler und alle Terme im Nenner durch den Term mit der höchsten Potenz, der in \( x^4 \)
\( \lim_{x\to +\infty} \dfrac{-x^3+2x-1}{x^4 - 3 x^3 + 9 } = \lim_{x\to +\infty} \dfrac{ \dfrac{-x^3}{x^4}+\dfrac{2x}{x^4}-\dfrac{1}{x^4}}{\dfrac{x^4}{x^4} - \dfrac{3 x^3}{x^4} + \dfrac{9}{x^4} }\).
Vereinfachen Sie rationale Begriffe
\( = \lim_{x\to +\infty} \dfrac{\dfrac{-1}{x}+\dfrac{2}{x^3}-\dfrac{1}{x^4}}{1 - \dfrac{3}{x} + \dfrac{9}{x^4} } = \dfrac{0+0-0}{1 - 0 + 0 } = \dfrac{0}{1} = 0\)
c)
Der Grenzwert hat die unbestimmte Form \( \infty \cdot 0 \).
Sei \( t = \dfrac{3}{x} \) und schreibe den Grenzwert in Form von t um.
\( \lim_{x\to +\infty} x \sin(\dfrac{3}{x}) = \lim_{t\to 0} 3 \dfrac {\sin(t)}{t} \).
Unter Verwendung des bekannten Ergebnisses \( \lim_{t\to 0} \dfrac {\sin(t)}{t} = 1 \) ergibt sich der Grenzwert zu
\( = 3 \times 1 = 3\)
d)
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \dfrac{0}{0}\), unbestimmte Form
Verwenden Sie die a L'Hospital-Regel für die unbestimmte Form, die wir schreiben können
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \lim_{x\to 0} \dfrac{ d (\sin(x)+x) / dx }{ d(2x^2+x)/dx} = \lim_{x\to 0} \dfrac{ cos(x)+ 1 }{ 4x+1} = \dfrac{ cos(0)+ 1 } { 4\times 0+1} = 2\)
e)
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} \).
Es ist bekannt, dass der Bereich von \( \sin(x) \) gegeben ist durch
\( -1 \le \sin(x) \le 1 \)
Addiere 1 zu allen Termen der Ungleichung, um die folgende Ungleichung zu erhalten
\( -1 + 1 \le \sin(x) + 1 \le 1 + 1 \)
\( 0 \le \sin(x) + 1 \le 2 \)
Teilen Sie alle Terme der obigen Ungleichung durch das positive \( x \)
\( \dfrac{0}{x} \le \dfrac{\sin(x) + 1}{x} \le \dfrac{2}{x} \)
Es gilt \( \lim_{x\to +\infty} \dfrac{0}{x} = 0 \) und \( \lim_{x\to +\infty} \dfrac{2}{x} = 0 \)
Mit dem Satz Squeezing (oder Sandwich) können wir den gegebenen Grenzwert wie folgt auswerten
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} = 0 \)
Solution to Question 5
a)
Der Graph von \( y = e^{x-1} \) und \( y = x \) ist unten dargestellt. Die Ableitung von \( y = e^{x-1} \) ist gleich \( y ' = e^{x-1} \) und die Steigung \( m \) der Tangente bei \( x = 1 \) ist der Wert der Ableitung bei \( x = 1\). Somit
\( m = e^{1-1}= 1 \)
Die Gleichung der Tangente am Punkt \( (1,1) \) ist gegeben durch
\( y - 1 = 1 \times (x - 1) \)
Was vereinfacht
\( y = x \)
Daher sind die Graphen von \( y = e^{x-1} \) und \( y = x \) tangential im Punkt \( (1,1) \) und wir können daher grafisch darstellen, dass \( e^ {x-1} \ge x \).
b)
Die erste und zweite Ableitung von \( f \) sind gegeben durch
\( f'(x) = \dfrac{x^2}{2}-e^{x-1} \)
\( f''(x) = x-e^{x-1} \)
Ein Wendepunkt tritt bei einem Wert von \( x \) auf, wobei \( f''(x ) \) Vorzeichen ändern. Wir haben in Teil a) gesehen, dass \( e^{x-1} \ge x \) geschrieben werden kann als
\( x-e^{x-1} \le 0 \)
und daher ist \( f''(x) \) negativ und hat eine Nullstelle bei \( x = 1 \). Daher ist der Graph von \( f(x) \) nach unten konkav und hat keinen Wendepunkt, da \( f''(x) \) das Vorzeichen nicht ändert.
Lösung zu Frage 6
a) Die Summe Regel von Ableitungen ergibt: \( f'(x) = e^{x-1 } + \dfrac{3}{3x-1} + 2 \cos(2x+1) \)
b) Produkt der Ableitungsregel: \( g'(x) = 4(2x-1)(\tan(x)-1) + (2x-1)^2(\sec^2(x)) \)
c) Quotienten-Ableitungs-Regel: \( h'(x) = \dfrac{ (1 + \sin(x))(x^2-2x+1) - (x - \cos(x))(2x-2 ) }{(x^2-2x+1)^2} \)
d) Sei \( u = \sqrt{x^3 - \dfrac{1}{x} + 2} \), schreibe die Funktion \(m \) als \(m = \sin u \) und verwende dann das Kettenregel von Ableitungen
e)
Schreiben Sie \( 3^{ 2x+3} \) und \( \log_3(2x-1) \) um als
\( 3^{2x+3} = e^{(2x+3) \ln 3}\) , Änderung der Basis von Exponentialfunktionen
\( \log_3(2x-1) = \dfrac{ \ln(2x-1)}{ \ln 3}\) , Basiswechsel von Logarithmen
Ersetzen Sie \( n(x) \) und schreiben Sie es um als
\( n(x) = 3^{ 2x+3} + \log_3(2x-1) = e^{(2x+3) \ln 3} + \dfrac{ \ln(2x-1)}{ \ln 3} \)
Wir berechnen nun die Ableitung
\( n'(x) = ( 2 \ln 3 ) e^{(2x+3) \ln 3} + \dfrac{1}{ \ln 3} \dfrac{2}{2x-1} = ( 2 \ln 3 ) 3^{2x+3} + \dfrac{2}{\ln 3(2x-1)} \)
Lösung zu Frage 7
Wir differenzieren zunächst die gegebene Gleichung implizit
\( 2 y \dfrac{d y}{d x} cos(y^2) = 2 x \)
\( \dfrac{d y}{d x} = \dfrac{ x}{ y cos(y^2)} \)
Die Steigung \( m \) der Tangente ist durch den Wert von \( \dfrac{d y}{d x} \) am Punkt \( ( 0,\sqrt{\pi}) \) gegeben.
\( m = \dfrac{(0)}{\sqrt{\pi} cos((\sqrt{{\pi}})^2)} = 0 \)
Die Gleichung der Tangente an die Kurve am Punkt \( ( 0,\sqrt{\pi}) \) in Punktsteigungsform ist gegeben durch
\( y - \sqrt{\pi} = 0(x - 0) \)
Es ist eine horizontale Linie, gegeben durch
\( y = \sqrt{\pi} \)
Lösung zu Frage 8
\( f(x) \) ist stetig auf den Intervallen \( (-\infty , 1) \) , \( (1,2) \) und \( (2 , +\infty) \). Wir müssen \( a \) und \( b \) finden, damit es auch bei \( x = 1 \) und \( x = 2 \) stetig ist und daher auf \( (-\infty , +\infty ) \).
\( f(1) = 1 \)
\( \lim_{x\to 1^-} f(x) = 1 \)
\( \lim_{x\to 1^+} f(x) = a(1)^3+b = a + b \)
Die Grenzen links und rechts von \( 1 \) müssen gleich sein
\( a + b = 1 \) (Gleichung 1)
\( f(2) = 2 + 2 b \)
\( \lim_{x\to 2^-} f(x) = a(2)^3 + b = 8 a + b \)
\( \lim_{x\to 2^+} f(x) = 2 + 2 b \)
Die Grenzen von links und rechts von \( 2 \) müssen gleich sein
\( 8 a + b = 2 + 2 b \) (Gleichung 2)
Lösen Sie die Gleichungen (1) und (2) gleichzeitig, um sie zu finden
\( a = \dfrac{1}{3} \) und \( b = \dfrac{2}{3} \)
Lösung zu Frage 9
Finden Sie die Ableitung von \( y \).
\( y' = 1 + \cos(x) \)
Die Steigung \( m \) der Tangente bei \( x = 0 \) ist gleich dem Wert von \( y' \) bei \( x = 0 \). Somit
\( m = 1 + \cos(0) = 2 \)
Die y-Koordinate des Tangentialpunktes \( P \) ist durch den Wert von \( y \) bei \( x = 0 \) gegeben. Somit
\( P(0 , 0 + \sin(0)) = P(0,0) \)
Die Gleichung der Tangente in Punktsteigungsform ist gegeben durch
\( y - 0 = 2(x - 0) \)
und in Steigungsabschnittsform
\( y = 2 x \)
Lösung zu Frage 10 Definition der Ableitung \( f' \) der Funktion \( f \) ist durch den Grenzwert gegeben
\( f'(x) = \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \)
Ersetzen Sie \( f(x) \) durch \( \sqrt{x+2} \) in der obigen Definition, um zu erhalten
\( f'(x) = \lim_{h\to 0} \dfrac{\sqrt{x + h +2}- \sqrt{x+2} }{h} \)
Der obige Grenzwert hat die unbestimmte Form \( \dfrac{0}{0} \). Multiplizieren Sie Zähler und Nenner mit dem Konjugat des Zählers
\( f'(x) = \lim_{h\to 0} \dfrac{ (\sqrt{x + h +2}- \sqrt{x+2} ) (\sqrt{x + h +2} + \ sqrt{x+2} ) }{h(\sqrt{x + h +2} + \sqrt{x+2} )} \)
Erweitern Sie den Zähler und vereinfachen Sie
\( f'(x) = \lim_{h\to 0} \dfrac{ (x + h + 2)- (x + 2) ) }{h(\sqrt{x + h +2} + \sqrt{ x+2} )} = \lim_{h\to 0} \dfrac{ h }{h(\sqrt{x + h +2} + \sqrt{x+2} )}\)
Zähler und Nenner durch \( h \) dividieren (oder \( h \) aufheben)
\( f'(x) = \lim_{h\to 0} \dfrac{ 1 }{\sqrt{x + h +2} + \sqrt{x+2} }\)
Bewerten Sie den Grenzwert und damit die Ableitung
\( f'(x) = \dfrac{ 1 }{ \sqrt{x + 0 + 2} + \sqrt{x + 2} } = \dfrac{ 1 }{2 \sqrt{x + 2} }\)
Lösung zu Frage 11
Finden Sie die erste und zweite Ableitung
\( f'(x) = e^x (x^2-5x+8) + e^x (2 x -5) +\dfrac{x^3}{3}-\dfrac{x^2}{ 2} = e^x (x^2-3x+3)+\dfrac{x^3}{3}-\dfrac{x^2}{2} \)
\( f''(x) = e^x(x^2-3x+3)+e^x(2x-3) + x^2-x = e^x(x^2-x)+x^ 2-x = x (x - 1) e^x \)
\( f'' \) hat zwei Nullstellen: \( x = 0 \) und \( x = 1\) und \( e^x \) ist immer positiv. Daher hat die Zeichentabelle von \( f'' \) drei Intervalle
1) \( (-\infty , 0 ) \) , Testwert \( x = -1 \) , \( f''(-1) = 2/e \) , also \( f''(x) \) ist positiv im Intervall \( (-\infty , 0 ) \).
2) \( (0 , 1 ) \) , Testwert \( x = 1/2 \) , \( f''(1/2) = -\dfrac{\sqrt 2}{4} \) , also \( f''(x) \) ist negativ auf dem Intervall \( (0 , 1 ) \).
3) \( (1 , +\infty ) \) , Testwert \( x = 2 \) , \( f''(2) = 2e^2 \) , \( f''(x) \) ist positiv auf dem Intervall \( (1 , +\infty ) \).
\( f'' \) ist konkav auf den Intervallen \( (-\infty , 0 ) \) und \( (1 , +\infty ) \) und konkav nach unten auf das Intervall \( (0 , 1 ) \).
\( f'' \) ändert das Vorzeichen bei \( x = 0 \) und \( x = 1 \) und hat daher Wendepunkte bei \( x = 0 \) und \( x = 1 \).
Lösung zu Frage 12 Newtons Methode basiert auf dem folgenden Algorithmus: Kenntnis einer Näherung \( x_n \) an die Lösung von an Gleichung \( f(x) = 0 \), die nächste Näherung \( x_{n+1}\) an die Gleichung ist gegeben durch
\( x_{n+1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \).
Die Lösung der gegebenen Gleichung \( e^x = x^3 \) ist gleich der Lösung der Gleichung \( f(x) = e^x - x^3 = 0 \)
\( f'(x) = e^x - 3x^2 \)
Wir kennen eine erste Näherung \( x_1 = 2 \); Mit dem Newton-Algorithmus approximieren wir \( x_2\) durch
\( x_{2} = x_1 - \dfrac{f(x_1)}{f'(x_1)} = 2 - \dfrac{e^2 - 2^3}{e^2 - 3 \times 2^2} \approx 1,87 \) (auf zwei Dezimalstellen gerundet)
Eine Näherung \(x_3\) kann unter Verwendung von \( x_2 \) oben usw. erhalten werden.
Lösung zu Frage 13
Finden Sie die erste Ableitung und faktorisieren Sie sie.
\( f'(x) = 4 x^3 - 3 x^2 = x^2(4x - 3)\)
\( f'(x) \) hat zwei Nullstellen bei \( x = 0 \) und \( x = 3/4 \) und beide liegen innerhalb des Intervalls \( [0,5] \). Die Nullstellen von \( f'(x) \) heißen kritische Punkte.
Wir werten nun die Funktion an den Endpunkten des angegebenen Intervalls und den Nullstellen von \( f'(x) \) aus.
\( f(0) = 0 \)
\( f(5) = 5^4 - 5^3 = 500 \)
\( f(3/4) = (3/4)^4 - (3/4)^3 = -\dfrac{27}{256} \)
Beim Vergleich dieser Werte hat \( f(x) \) ein absolutes Maximum gleich \(500 \) am Endpunkt \( x = 5 \) und ein absolutes Minimum gleich \( -\dfrac{27}{256} \) am kritischen Punkt \( x = 3/4 \)
Weitere Fragen zum absoluten Minimum und Maximum einer Funktion enthalten.
Lösung zu Frage 14
Das Volumen \( V \) eines rechteckigen Kastens mit den Abmessungen \( L \),\( W \) und \( H\) ist gegeben durch
\( V = L(t) W(t) H(t) \)
wobei \( L(t)\) , \( W(t) \) und \( H(t) \) Funktionen der Zeit \( t \) sind.
Da sich die Abmessungen des Kastens mit der Zeit ändern, ändert sich auch das Volumen des Kastens mit der Zeit mit der Änderungsrate von \( V\) ist durch die erste Ableitung \( \dfrac{dV}{dt} \) gegeben.
\( \dfrac{dV}{dt} = W(t) H(t) \dfrac{d L}{dt } + L(t) H(t) \dfrac{d W}{dt } + L(t ) W(t) \dfrac{d H}{dt } \)
Ersetzen Sie die bekannten Größen durch ihre Zahlenwerte
\( \dfrac{dV}{dt} = 8 \times 5 \times 0,1 + 20 \times 5 \times (-0,2) + 20 \times 8 \times 0,3 = 32 \; cm^3 / sec \)
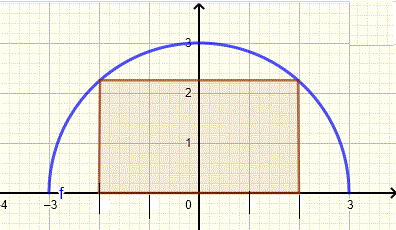
Lösung zu Frage 15 Gleichung eines Kreises mit Radius \( 3 \) und Mittelpunkt bei \( (0 , 0) \) gegeben von
\( x^2 + y^2 = 3^2 \)
Lösen Sie die obige Gleichung für y
\(y^2 = 9 - x^2\)
\( y = \pm \sqrt{9 - x^2} \)
Die Gleichung für den oberen Halbkreis lautet
\( y = \sqrt(9-x^2) \)
Ein Punkt auf dem Halbkreis mit der x-Koordinate \( x \) hat eine y-Koordinate gleich \(\sqrt{9 - x^2} \) (siehe Grafik unten)
Das Rechteck hat eine Länge \( L = 2x \) und eine Breite (oder Höhe) \( W = \sqrt(9-x^2) \). Die Fläche \( A \) des Rechtecks ist gegeben durch
\( A(x) = L \times W = 2 x \sqrt(9-x^2) \) , \( 0 \le x \le 3 \)
Finden Sie die erste Ableitung von \( A \)
\( \dfrac{d A}{dx} = 2\sqrt{9-x^2} + (2x) (\dfrac{1}{2}) (-2x) (9-x^2)^{- 1/2} =\dfrac{2\left(-2x^2+9\right)}{\sqrt{9-x^2}} \)
Nullstellen von \( \dfrac{d A}{dx} \) werden durch die Nullstellen des Zählers von \( \dfrac{d A}{dx} \) gegeben
\( -2x^2+9 = 0 \)
Ergibt zwei Nullen: \( x = \sqrt{4.5} \) und \( x = - \sqrt{4.5} \)
Wir betrachten die Nullstelle bei \( x = \sqrt{4,5} \), da sie innerhalb des Intervalls \( [0 , 3 ] \) liegt
Wir werten nun die Fläche \( A(x) \) an den Endpunkten \( x = 0 \) und \( x = 3 \) und am kritischen Punkt \( x = \sqrt{4,5} \) aus.
\( A(0) = 0 \)
\( A(3) = 0 \)
\( A(\sqrt{4,5}) = 9 \)
Die Fläche A ist maximal für \( x = \sqrt{4,5} \)
Die Abmessungen sind:
\( L = 2 x = 2 \sqrt{4,5} \approx 4,24 \)
\( W = \sqrt(9-x^2) = \sqrt(9-\sqrt{4,5}^2) \approx 2,12 \)
Weitere Optimierungsprobleme enthalten.
\( \)\( \)\( \)\( \)\( \)
