Geometrieprobleme mit Lösungen und Antworten

Löse die lineare Gleichung \( x - y = 1 \) nach \( x \) auf:

\( x = 1 + y \)

Setze dies in die Standardgleichung des gegebenen Kreises ein:

\[ (1 + y)^2 + 2(1 + y) + y^2 + 4y = -1 \]

Erweitere und vereinfache den Ausdruck. Fasse gleiche Terme zusammen und schreibe die resultierende quadratische Gleichung in Standardform:

\[ 2y^2 + 8y + 4 = 0 \]

Löse die quadratische Gleichung, um die Werte für \( y \) zu erhalten:

\[ y = -2 \pm \sqrt{2} \]

Verwende die Substitution \( x = 1 + y \), um die entsprechenden \( x \)-Werte zu finden.

Daher sind die Schnittpunkte zwischen der Geraden und dem Kreis:

\[ (-1 + \sqrt{2},\ -2 + \sqrt{2}) \quad \text{und} \quad (-1 - \sqrt{2},\ -2 - \sqrt{2}) \]

Um die Fläche des Dreiecks zu finden, das von den Geraden \( y = x \) und \( y = -2x + 3 \) gebildet wird, zeichne zuerst beide Geraden.

Löse das Gleichungssystem, um den Schnittpunkt zu finden:

\[ y = x \quad \text{und} \quad \; y = -2x + 3 \]

Durch Lösen erhalten wir den Schnittpunkt \( (1,\ 1) \). Die Höhe des Dreiecks ist 1 (die y-Koordinate).

Den x-Achsenabschnitt von \( y = -2x + 3 \) erhält man durch Setzen von \( y = 0 \): \[ 0 = -2x + 3 \Rightarrow x = \dfrac{3}{2} \]

Die Basis des Dreiecks ist \( \dfrac{3}{2} \). Somit ist die Fläche:

\[ \text{Fläche} = \dfrac{1}{2} \times \text{Basis} \times \text{Höhe} = \dfrac{1}{2} \times \dfrac{3}{2} \times 1 = \dfrac{3}{4} \]

Die Sinussatzformel für die Fläche eines Dreiecks mit zwei Seiten und dem eingeschlossenen Winkel lautet:

\[ 18 = \dfrac{1}{2} \times 5 \times 10 \times \sin(A) \]

Löst man nach \( \sin(A) \) auf, erhält man:

\[ \sin(A) = \dfrac{18}{25} \]

Wir verwenden nun den Kosinussatz, um die Länge \( x \) der dritten Seite gegenüber dem Winkel \( A \) zu finden:

\[ x^2 = 5^2 + 10^2 - 2 \times 5 \times 10 \times \cos(A) \]

Da \( \cos(A) = \sqrt{1 - \sin^2(A)} \), setzen wir ein:

\[ \cos(A) = \sqrt{1 - \left(\dfrac{18}{25}\right)^2} \]

Setze \( \cos(A) \) in den Kosinussatz ein und löse nach \( x \) auf:

\[ x \approx 7.46 \quad \text{(gerundet auf 3 signifikante Ziffern)} \]

Die Fläche des Dreiecks BOC beträgt 15 und ist gegeben durch \[ \text{Fläche}_{\triangle BOC} = \dfrac{1}{2} \cdot BO \cdot OC \cdot \sin(\angle BOC) \]

Die Fläche des Dreiecks AOD ist gegeben durch \[ \text{Fläche}_{\triangle AOD} = \dfrac{1}{2} \cdot AO \cdot OD \cdot \sin(\angle AOD) \]

Beachte, dass die Winkel \( \angle BOC \) und \( \angle AOD \) gleich sind.

Nach dem Satz der sich schneidenden Sehnen gilt: \[ AO \cdot OC = BO \cdot OD \]

Dies kann geschrieben werden als: \[ \dfrac{AO}{BO} = \dfrac{OD}{OC} = \dfrac{10}{5} = 2 \]

Die Verhältnisse \( \dfrac{AO}{BO} \) und \( \dfrac{OD}{OC} \) sind beide gleich 2, daher ist ihr Produkt: \[ \dfrac{AO \cdot OD}{BO \cdot OC} = 4 \]

Daraus folgt: \[ AO \cdot OD = 4 \cdot (BO \cdot OC) \]

Daher ist die Fläche des Dreiecks AOD viermal so groß wie die Fläche des Dreiecks BOC: \[ \text{Fläche}_{\triangle AOD} = 4 \cdot 15 = 60 \]

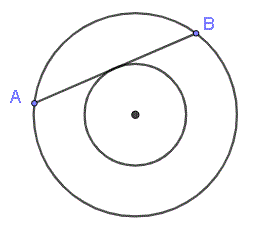
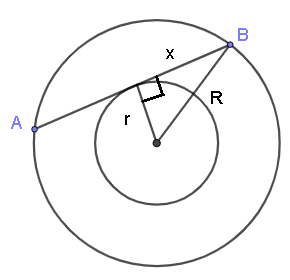
Wenn wir im kleinen Kreis einen Radius zum Berührungspunkt zeichnen, steht er im rechten Winkel zur Sehne (siehe Abbildung unten). Wenn \( x \) die halbe Länge von \( AB \) ist, \( r \) der Radius des kleinen Kreises und \( R \) der Radius des großen Kreises, dann gilt nach dem Satz des Pythagoras:

\[ r^2 + x^2 = R^2 \]

\[ 6^2 + x^2 = 10^2 \]

Löse nach \( x \) auf: \( x = 8 \)

Länge von \( AB = 2x = 16 \)

Verwende den Kosinussatz im Dreieck ABE:

\[ 13^2 = 20^2 + 9^2 - 2(20)(9)\cos(T) \tag{I} \]

Verwende den Kosinussatz im Dreieck ACB:

\[ x^2 = 20^2 + 9^2 - 2(20)(9)\cos(90^\circ - T) \]

Beachte, dass \( \cos(90^\circ - T) = \sin(T) \) und schreibe die zweite Gleichung um als:

\[ x^2 = 20^2 + 9^2 - 2(20)(9)\sin(T) \tag{III} \]

Löse Gleichung (I) nach \( \cos(T) \) auf:

\[ \cos(T) = \dfrac{13}{15} \]

Verwende die trigonometrische Identität \( \sin(T) = \sqrt{1 - \cos^2(T)} \), um zu finden:

\[ \sin(T) = \dfrac{2\sqrt{14}}{15} \]

Setze \( \sin(T) = \dfrac{2\sqrt{14}}{15} \) in Gleichung (III) ein und löse nach \( x \) auf:

\[ x = \sqrt{481 - 48\sqrt{14}} \approx 17.4 \]

(Gerundet auf 3 signifikante Ziffern.)

a) Volumen des zusammengesetzten Körpers

1. Volumen des Zylinders:

\[ V_{\text{Zylinder}} = \pi r^2 h = \pi (5)^2 (12) = \pi (25)(12) = 300\pi \, \text{cm}^3 \]

2. Volumen der Halbkugel:

\[ V_{\text{Halbkugel}} = \frac{1}{2} \left( \frac{4}{3} \pi r^3 \right) = \frac{2}{3} \pi (5)^3 = \frac{2}{3} \pi (125) = \frac{250}{3} \pi \, \text{cm}^3 \]

3. Gesamtvolumen:

\[ V_{\text{gesamt}} = V_{\text{Zylinder}} + V_{\text{Halbkugel}} = 300\pi + \frac{250}{3}\pi = \left( \frac{900 + 250}{3} \right)\pi = \frac{1150}{3} \pi \, \text{cm}^3 \]

b) Masse des Objekts

\[ \text{Masse} = \text{Dichte} \times \text{Volumen} = 7.8 \times \frac{1150}{3} \pi \]

Näherung mit \(\pi \approx 3.1416 \):

\[ \text{Masse} \approx 7.8 \times \frac{1150}{3} \times 3.1416 \approx 9396.66 \, \text{g} \]

a) Fläche des Gartens

1. Fläche des Rechtecks:

\[ A_{\text{Rechteck}} = \text{Länge} \times \text{Breite} = 12 \times 8 = 96 \, \text{m}^2 \]

2. Fläche des Halbkreises (mit Radius \(r = 4\) Meter):

\[ A_{\text{Halbkreis}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (4)^2 = \frac{1}{2} \pi (16) = 8\pi \, \text{m}^2 \]

3. Gesamtfläche:

\[ A_{\text{gesamt}} = A_{\text{Rechteck}} + A_{\text{Halbkreis}} = 96 + 8\pi \, \text{m}^2 \]

Mit \(\pi \approx 3.1416\):

\[ A_{\text{gesamt}} \approx 96 + 8(3.1416) = 96 + 25.13 = \boxed{121.13 \, \text{m}^2} \]

b) Umfang des Gartens

Hinweis: Wir lassen die gemeinsame Kante zwischen Halbkreis und Rechteck weg.

1. Drei Seiten des Rechtecks (ohne die 8-m-Seite):

\[ P_{\text{Rechteck}} = 12 + 8 + 12 = 32 \, \text{m} \]

2. Gebogener Teil des Halbkreises:

\[ P_{\text{Halbkreis}} = \frac{1}{2} (2\pi r) = \pi r = \pi \cdot 4 = 4\pi \, \text{m} \]

3. Gesamtumfang:

\[ P_{\text{gesamt}} = 32 + 4\pi \approx 32 + 12.566 = \boxed{44.57 \, \text{m}} \]