Solutions to Grade 10 Math Practice Test Questions

Solutions to Grade 10 math practice test questions including algera, trigonmetry and geometry are presented.

Solution
Solve the systems of equations.

a)

Expand the left sides and rewrite the system of equations in standard form with constant terms on the right.

Add the left terms together and the right terms together of equations (I) and (II) in order to eliminate the terms with x.

Simplify to obtain an equation with one unknown.

Solve for y to obtain

 Substitute $ y = 0 $ in either equation (I) ( or (II) ) to obtain
$ \quad -2x-(0) = 2 $

Solve the above equation for $ x $ to obtain
$ \quad x = - 1 $

The solution to the given system of equations is the ordered pair
\[ (-1,0) \]

b)
$ \quad \begin{cases} \displaystyle \frac{x-1}{3} + y & = & 5 \\ 2(x+3) - \frac{y}{5} & = & 7\end{cases} $

In order to eliminate the denominators in the two equations in the given system, multiply all terms of the first equation by $ 3 $ and multiply all terms of the second equation by $ 5 $.
$ \quad \begin{cases} \displaystyle \color{red}{3}\frac{x-1}{3} + \color{red}{3} y & = & \color{red}{3} \cdot 5 \\ \displaystyle \color{red}{5} ( 2(x+3) ) - \color{red}{5} \frac{y}{5} & = & \color{red}{5} \cdot 7\end{cases} $

Expand, simplify and rewrite the system of equations in standard form.
$ \quad \begin{cases} \displaystyle x + 3 y & = & 16 \\ 10 x - y & = & 5\end{cases} $

In order to eliminate the terms in $ y $, multiply all terms of the second equation by 3.
$ \quad \begin{cases} \displaystyle x + 3 y & = & 16 \\ \color{red}3(10 x - y) & = & \color{red}3 \cdot 5\end{cases} $

Expand
$ \quad \begin{cases} \displaystyle x + 3 y & = & 16 \qquad (I) \\ 30 x - 3y & = & 15 \qquad (II) \end{cases} $

Add left sides of the equations together and the right sides together to eliminate the terms in y.
$ \quad 31 x = 31 $

Solve for $ x $
$ \quad x = 1 $

Substitute $ x = 1 $ in equation (I) (or equation (II) )
$ \quad (1) + 3 y = 16 $

Solve for $ y $
$ \quad y = 5 $

The solution to the given system of equations is the ordered pair
\[ (1,5) \]

c)
$ \displaystyle \quad \begin{cases} (x-1)^2 + y & = & -1 \qquad (I) \\ - 4 x + 2y & = & -6 \qquad (II) \end{cases} $

Solve equation (II) for y to obtain
$ \quad y = 2x - 3 \qquad (III) $

Substitute $ y = 2x - 3 $ in equation (II) and rewrite as
$ \quad (x-1)^2 + \color{red}{(2x - 3)} = -1 $

Expand and rewrite in standard form $ \quad x^2 - 1 = 0 $

Solve the above equation for $ x $ to obtain the solutions $ \quad x = 1 $ and $ x = - 1$

Having found the solutions $ x $, we substitute each value of the solutions $ 1 $ and $ -1 $ in equation (III) to obtain the corresponding values of the solutions $ y $.
Substitute $ x = 1 $ in equation (III) to obtain
$ \quad y = 2(1) - 3 = -1 $

Substitute $ x = - 1 $ in equation (III) to obtain
$ \quad y = 2(-1) - 3 = - 5 $

The two ordered pairs that are solutions to the given system of equations are
\[ (1,-1) \quad \text{and} \quad (-1,-5) \]
Solution
Expand and simplify the expressions.
a)
$ \quad -(x+2)(x-1) + (x-2)^2 $

Expand the product $ (x+2)(x-1) $ and the square $ (x-2)^2 $
$ \quad (x+2)(x-1) = x^2+x-2 $
$ \quad (x-2)^2 = x^2 - 4x + 4 $

Substitute the above in the given expression
$ \quad -(x+2)(x-1) + (x-2)^2 = - (x^2+x-2 ) + (x^2 - 4x + 4 ) $

Take out the brackets changing the signs for expressions with the minus sign in front.
$ \quad -(x+2)(x-1) + (x-2)^2 = - x^2 - x + 2 + x^2 - 4x + 4 $

Group like terms and simplify.
\[ \quad -(x+2)(x-1) + (x-2)^2 = -5x+6 \]

b)
$ \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) $
Expand the products $ (x-2)(x^2 + 3x -3) $ and $ (x-1)(x+1) $.
$ \quad (x-2)(x^2 + 3x -3) = x^3+x^2-9x+6 $
$ \quad (x-1)(x+1) = x^2 - 1$

Substitute the above in the given expression
$ \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) = (x^3+x^2-9x+6) - (x^2 - 1) $

Take out the brackets changing the signs for expressions with the minus sign in front.
$ \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) = x^3+x^2-9x+6 - x^2+1 $

Group like terms and simplify.
\[ \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) = x^3-9x+7 \]
Solution
Factor completely the expressions.
a)
$ \quad 3x^3+6x^2 $

Rewrite each term as a product of prime factors
$ \quad 3x^3 = 3 \cdot x \cdot x \cdot x $
$ \quad 6x^2 = 2 \cdot 3 \cdot x \cdot x $
Identify all common factors
$ \quad 3x^3 = \color{red}3 \cdot \color{red}x \cdot \color{red}x \cdot x $
$ \quad 6x^2 = 2 \cdot \color{red} 3 \cdot \color{red}x \cdot \color{red}x $
The greatest common factor is
$ \quad 3 \cdot x \cdot x $
Substitute each term by its factored form and rewrite the given expression as
$ \quad 3x^3+6x^2 = \color{red}3 \cdot \color{red}x \cdot \color{red}x \cdot x + 2 \cdot \color{red} 3 \cdot \color{red}x \cdot \color{red}x $
Factor out the common factor $ \color{red} 3 \cdot \color{red}x \cdot \color{red}x $ and rewrite the above as
$ \quad 3x^3+6x^2 = \color{red} 3 \cdot \color{red}x \cdot \color{red}x (x+2) $
Noting that $ 3 \cdot x \cdot x = 3 x^2 $, the given expression in factored form is written as
\[ \quad 3x^3+6x^2 = 3 x^2 (x+2) \]

b)
$ \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) $
Factor out $ (x-3) $
$ \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) = (x-3)(x^2 + 3x + 2- (x+1)) $

Simplify the $ (x^2 + 3x + 2- (x+1)) $ and rewrite the above as
$ \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) = (x-3)(x^2+2x+1) $

Note that $ x^2+2x+1 = (x+1)^2 $, hence \[ \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) = (x-3)(x+1)^2 \]

c)
$ \quad 81 x^2 - 16 y^2$
Noting that $ 81 = 9^2 $, $ x^2 = x^2 $, $ 16 = 4^2 $ and $ y^2 = y^2 $, rewrite the given expression as the difference of two squares
$ \quad 81 x^2 - 16 y^2 = (9x)^2 - (4y)^2 $
We now use the identity related to the difference of two squares given by $ a^2 - b^2 = (a-b)(a+b) $ to factor the above expression
\[ (9x)^2 - (4y)^2 = (9x - 4y)(9x + 4y) \]

d)
$ \quad -6x^2+7x-2 $
Factor the minus sign out
$ \quad -6x^2+7x-2 = - (6x^2 - 7 x + 2) \qquad (I) $

To factor $ 6x^2 - 7 x + 2 $, we need to write as $ \quad 6x^2 - 7 x + 2 = ( ax + b) (c x + d) $
where the product $ b \cdot d = 2 $ which means either $ b = 1 $ and $ d = 2 $ or $ b = - 1 $ and $ d = - 2 $
The product $ a \cdot c = 6 $ means the following possible values: $ a = 1 $ and $ c = 6 $, or $ a = 2 $ and $ c = 3 $ or $ a = 3 $ and $ c = 2 $

After substitutions of values of $ a, b, c ,d $, we end up with the factored form
$ \quad 6x^2 - 7 x + 2 = (2x-1)(3x-2) $
Substitute in (I) above \[ \quad -6x^2+7x-2 = - (2x-1)(3x-2) \]
Solution
Given $ f(x) = -2 x^2 - 2 x + 4 $, find
a) the vertex of the graph of $ f $,
b) The x and y intercepts of the graph of function $ f(x) = -2 x^2 - 2 x + 4 $,
c) The axis of symmetry of the graph of $ f $.
d) Use a calculator to graph $ f $ and check the answers to parts a) , b) and c).

a)
$ f $ is a quadratic function and its graph is a parabola.
We first write the given function in standard vertex form $ \; f(x) = a (x - h)^2 + k \; $ by completing the square , where the vertex has the coordinates $ (h,k) $.

Factor $ -2 $ out of the terms with $ x $ and $ x^2$ in $ \; f(x)$
$ \quad f(x) = - 2 (x^2 + x) + 4 $

Complete the square of the expression inside the parenthesis.
$ \quad \displaystyle \quad f(x) = - 2 \left( \left(x + \frac{1}{2}\right)^2 - 1/4 \right) + 4 $

Simplify and rewrite the above as
$ \quad \displaystyle \quad f(x) = - 2 \left(x + \frac{1}{2} \right)^2 + \frac{9}{2} $

Comparing the above function $ \; f(x) = - 2 \left(x + \frac{1}{2} \right)^2 + \frac{9}{2} \; $ with the standard vertex form $ \; f(x) = a (x - h)^2 + k \; $, we can write that $ h = - \frac{1}{2} $ and $ k = \frac{9}{2} $
Hence the vertex has the coordinates $ \displaystyle \left(- \frac{1}{2} , \frac{9}{2} \right) $

b)
The x intercepts, if any, are given by the solutions to the equation $ f(x) = 0 $, hence the equation
$ \quad \displaystyle \quad - 2 \left(x + \frac{1}{2} \right)^2 + \frac{9}{2} = 0 $
Which gives
$ \quad 2 \left(x + \frac{1}{2} \right)^2 = \frac{9}{2} $
$ \quad \left(x + \frac{1}{2} \right)^2 = \frac{9}{4} $
Solve by extracting the square root
$ \quad \left(x + \frac{1}{2} \right) = \pm \sqrt {\frac{9}{4}} $
Simplify to obtain the two solutions
$ \quad \left(x + \frac{1}{2} \right) = \pm \frac{3}{2} $
$ \quad x_1 = 1 $ and $ x_2 = - 2 $

The y intercept is given by $ y = f(0) = 4 $

c)
The axis of symmetry of the graph of $ f $ is give by the vertical line $ x = h = - \frac{1}{2} $
d)
The use of a graphing calculator gives the graph below where the vertex, the x and y intercepts and the axis of symmetry can all be verified to those calculated above.
Solution
Use proportionality to complete, if possible, the tables of values in a), b) and c).

a)
There are two types of proportionality rules:
1) $ y $ is directly proportional to $ x $ if there is a mathematical relationship between $ y $ and $ x $ of the form:
$ \quad \; y = k x \quad $ or $ \quad \displaystyle \frac{y}{x} = k \quad $ where $ k $ is a constant.
2) $ y $ is inversely proportional to $ x $ if there is a mathematical relationship between $ y $ and $ x $ of the form:
$ \quad \displaystyle y = \frac{k}{x} \quad $ or $ \quad y \cdot x = k \quad $ where $ k $ is a constant.

We complete table a), by calculating the ratio $ y / x $ and the product $ y x $ as shown below.

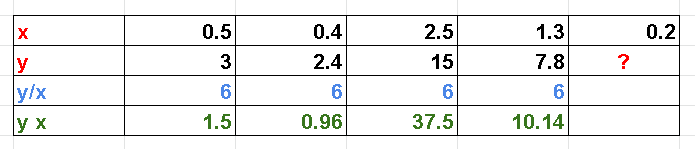
It can easily be seen that the ratio is constant such that $ \quad \displaystyle \frac{y}{x} = 6 \quad $ and hence there is a direct proportion between $ y $ and $ x $ given by
$ \quad \displaystyle y = 6 x \quad $
We now complete the table by calculating $ y $ for $ x = 0.2 $, \[ \displaystyle y = 6 \cdot 0.2 = 1.2 \quad \]

b)
We complete table b), by calculating the ratio $ y / x $ and the product $ y x $ as shown below.

It can easily be seen that the product is constant such that $ \quad y x = 0.2 \quad $ and hence there is an inverse proportion between $ y $ and $ x $ given by
$ \quad \displaystyle y x = 0.2 \quad $ or $ \quad \displaystyle y = \frac{0.2}{x} \quad $
We now complete the table by calculating $ y $ for $ x = 20 $, \[ \displaystyle y = \frac{0.2}{20} = 0.01 \quad \]

c)
We complete table c), by calculating the ratio $ y / x $ and the product $ y x $ as shown below.

It can easily be seen that neither the ratio$ \quad y / x $ nor the product $ y x $ is constant and therefore there is neither a direct nor an inverse proportion between $ y $ and $ x $ in the table. Hence we cannot calculate $ y $ for $ x = 11 $ in part c) because we do not know the relationship between $ y $ and $ x $.
Solution
Find all unknown sides and angles in the right triangle below.

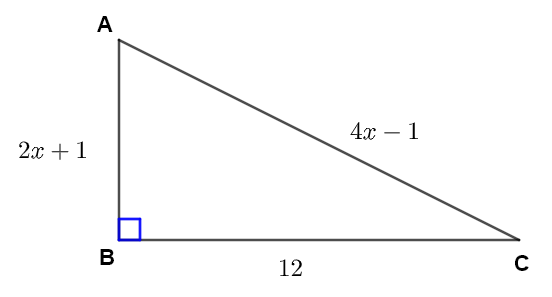
In order to find the unknown sides, we need to find $ x $.
The Pythagorean theorem applied to the given triangle gives:
$ \quad {\overline{AC}}^2 = {\overline{AB}}^2 + {\overline{BC}}^2 $
Substitute $ \overline{AC} , \overline{AB} $ and $ \overline{BC} $ by the given expressions and values to write the equation
$ \quad (4x-1)^2 = (2x+1)^2 + 12^2 $
Expand the square, group like terms, simplify and rewrite the equation in standard form.
$ \quad 12x^2-12x-144 = 0 $
Divide all terms of the equation by $ 12 $ and simplify
$ \quad x^2-x-12 = 0 $
Solve to obtain
$ \quad x = 4 $ and $ x = -3 $
The solution $ x = - 3 $ would give $ \overline{AC} = 4 x - 1 = -13 $ which is not acceptable since the length of the hypotenuse cannot be negative.
Let $ x = 4 $ and find the unknown side and the hypotenuse.
$ \quad \overline{AC} = 4 x - 1 = 15$
$ \quad \overline{AB} = 2x +1 = 9$
Using the definition of the tangent of angle $ ACB $, we have
$ \quad \displaystyle \tan \angle ACB = \frac{\overline{AB}}{\overline{BC}} = \frac{9}{12} = \frac{3}{4} $
Hence
$ \quad \angle ACB = \tan^{-1} \left(\frac{3}{4}\right) = 36.87^{\circ} $
Angles $ CAB $ and $ ACB $ are complementary and therefore
$ \quad \angle CAB = 90 - 36.87 = 53.13^{\circ} $
Solution
Angle $ \alpha $ is an acute angle such that $ \sin \alpha = 0.6 $. Find $ \cos \alpha$ and $ \tan \alpha$

Let us consider a right triangle with angle $ \alpha $ such that
$ \quad \displaystyle \sin \alpha = \frac{Opposite}{Hypotenuse} = \frac{a}{c} = \frac{0.6}{1} = 0.6 $

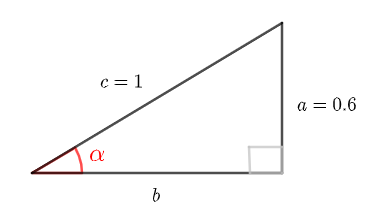
Use the Pythagorean theorem to find $ b $
$ \quad c^2 = a^2 + b^2 $
Substitute to find
$ \quad 1 = 0.6^2 + b^2 $
Solve for $ b^2 $
$ \quad b^2 = 1 - 0.36 = 0.64$
Solve for $ b $
$ \quad b = \sqrt {0.64} = 0.8$
We now use the definitions of cosine and sine
$ \quad \displaystyle \cos \alpha = \frac{Adjacent Side}{Hypotenus} = \frac {0.8}{1} = 0.8 $

$ \quad \displaystyle \tan \alpha = \frac{Opposite}{Adjacent} = \frac{0.6}{0.8} = \frac{3}{4} = 0.75 $
Solution
In the figure below, BE is parallel to CD. Find the lengths $ x $ and $ y $ of the segments CD and DE respectively.

The triangles $ ABE $ and $ ACD $ have a common angle $ A $.
Since $ BE $ is parallel to $ CD $, angles $ ABE $ and $ ACD $ are corresponding angles and therefore congruent.
Also angles $ AEB $ and $ ADC $ are corresponding angles and therefore congruent.
Triangles $ ABE $ and $ ACD $ have all three angles congruent and are therefore similar ..
Similar triangles have proportionality between the sides as follows
$ \quad \displaystyle \frac{\overline{AB}}{\overline{AC}} = \frac{\overline{BE}}{\overline{CD}} $
Substitute the known quantities to obtain the equation
$ \quad \displaystyle \frac{10}{10+2} = \frac{6}{X} $
$ \quad x = 7.2 $
The proportionality of the sides of the similar triangles also gives
$ \quad \displaystyle \frac{\overline{AE}}{\overline{AD}} = \frac{\overline{EB}}{\overline{DC}} $
Substitute the known quantities to obtain the equation
$ \quad \displaystyle \frac{11}{11+y} = \frac{6}{7.2} $
Solve for $ y = 2.2 $
Solution
The lengths of side AB and side BC of a triangle ABC are 14 cm and 10 cm respectively. The size of angle C is 49^o. Find all unknown angles and all unknown sides of the triangle.

Draw a triangle and label all known quantities.

Apply the sine rule
$ \quad \displaystyle \frac{c}{\sin C} = \frac{a}{\sin A} $
Solve for $ \sin A $
$ \quad \displaystyle \sin A = \frac {a}{c} \sin C $
Substitute and solve for $ A $
$ \quad \displaystyle A = \sin^{-1} \left(\frac {a}{c} \sin C \right) = \sin^{-1} \left(\frac {10}{14} \sin 49^{\circ} \right) = 32.62^{\circ}$
In any triangle the sum of all three angles $ A, B , C $ is equal to $ 180^{\circ} $; hence
$ \quad \displaystyle \angle A + \angle B + \angle C = 180^{\circ} $
Solve for angle $ B $
$ \angle B = 180 - (49 + 32.62) = 98.38^{\circ}$
Side $ b $ may be found using the sine law .
$ \quad \displaystyle \frac{b}{\sin B} = \frac{a}{\sin A} $
Solve for $ b $
$ \quad \displaystyle b = a \frac{\sin B}{\sin A} $
Substitute and simplify
$ \quad \displaystyle b = 10 \frac{\sin 98.38^{\circ}}{\sin 32.62^{\circ}} = 18.35$
NOTE that side $ b $ may be calculated using the cosine law as follows
$ \quad \displaystyle b^2 = a^2 + c^2 - 2 a c \cos B $
Substitute
$ \quad \displaystyle b^2 = 10^2 + 14^2 - 2 \cdot 10 \cdot 14 \cos 98.38^{\circ} = 336.80655$
Take the square root to find
$ \quad b = \sqrt {336.80655} \approx 18.35 $
Solution
Find the values of $ A $ and $ B $ if the line with equation $ A x + By = 1 $ passes through the points $ (1,5) $ and has a y-intercept at $ y = 3 $.

If the line passes through the points $ (1,5) $, then the x and y coordinates of this point satisfy the equation of the line. Hence substitute $ x $ and $ y $ by $ 1 $ and $ 5 $ respectively in the equation of the line to obtain the equation:
$ \quad A (1) + B(5) = 1 $
which may be written as
$ \quad A + 5 B = 1 $
The line has y-intercept at $ y = 3 $ is similar to saying that the line passes through the point $ (0 , 3) $, hence the equation
$ \quad A (0) + B(3) = 1 $
which may be written as
$ \quad 3 B = 1 $
Solve the above for $ B $ to obtain
$ \quad \displaystyle B = \frac{1}{3} $
Substitute $ B = \frac{1}{3} $ in the equation $ \quad A + 5 B = 1 $
$ \quad \displaystyle A + 5 \cdot \frac{1}{3} = 1 $
Solve for $ A $
$ \quad \displaystyle A = 1 - \frac{5}{3} = - \frac{2}{3} $
Solution
A chemist needs to make 5 L of 45%, by volume, of sulfuric acid solution. He has 20% and 55%, by volume, of sulfuric acid solutions available. He decides to mix the 20% and 55% solutions to make the 45% solution. How many liters of each solution must be mixed?

Let $ x $ be the number of liters of the $ 20\% $ sulfuric acid solution and $ y $ be the number of liters of the $ 55\% $ sulfuric acid solution.
We need to make a solution of 5 liters, hence the equation
$ \quad x + y = 5 \qquad (I) $
The amount of sulfuric acid in $ x $ and the amount of sulfuric acid $ y $ is equal to the amount of the sulfuric acid in the whole 5 liters; hence the equation
$ \quad 20\% \cdot x + 55\% \cdot y = 45\% \cdot 5 $
The last equation may be written as
$ \quad \displaystyle \frac{20 x}{100} + \frac{55 y}{100} = \frac{45 \cdot 5}{100} $
Multiply all terms of the above equation by $ 100 $ and simplify to eliminate the denominators and rewrite the equation as
$ \quad 20 x + 55 y = 225 \qquad (II) $
Equations (I) and (II) form a system of equations that needs to be solved.
Solve equation (I) for $ y $ to obtain
$ \quad y = 5 - x $
Substitute $ y = 5 - x $ in equation (II)
$ \quad 20 x + 55 (5 - x ) = 225 \qquad (II) $
Solve the above for $ x $
$ \quad x \approx 1.42 $ Liters
$ \quad y = 5 - 1.42 = 3.58 $ Liters
Hence we need to mix $ 1.42 $ Liters of a $ 20\% $ sulfuric acid solution and $ 3.58 $ Liters of a $ 55\% $ sulfuric acid solution to obtain a 5 Liters sulfuric acid solution with a concentration of $ 45\% $.
Solution
A family drove 1000 km from Paris to Prague in 10 hours. They drove part of the distance at an average speed of 80 km/h, and the rest at an average speed of 120 km/h. What distance did they drive at each speed ?

Let $ x $ and $ y $ be the distances driven at $ 80 $ km/h and $ 120 $ km/h respectively.
The time to drive distance $ x $ is given by (time = distance / speed )
$ \quad \displaystyle t_x = \frac{x}{80} $
The time to drive distance $ y $ is given by (time = distance / speed )
$ \quad \displaystyle t_y = \frac{y}{120} $
The total time to drive the total distance $ x + y = 1000 $ is given as $ t_1 + t_ 2 = 10 $ hours. Hence the system of equations

$\quad \displaystyle \left\{ \begin{aligned} x + y = 1000 \\ \frac{x}{80} + \frac{y}{120} = 10 \\ \end{aligned} \right.$
Multiply the second equation in the above system by the product $ 80 \cdot 120 $
$\quad \displaystyle \left\{ \begin{aligned} x + y = 1000 \\ \color{red}{80 \cdot 120}\frac{x}{80} + \color{red}{80 \cdot 120} \frac{y}{120} = \color{red}{80 \cdot 120} \cdot 10 \\ \end{aligned} \right.$

Simplify
$\quad \displaystyle \left\{ \begin{aligned} x + y = 1000 \\ 12 x + 8 y = 9600 \end{aligned} \right.$

Simplify
Solve the system by any method to obtain
$ y = 600 $ km and $ x = 400 $ km.
Solution
Triangle ABC has vertices at the points $ A(2,3) $, $ B(-3 , 4) $ and $ C $ located on the vertical line $ x = -1 $. Find all possible coordinates of point $ C $ so that $ ABC $ is a right triangle with hypotenuse $ AC $.

Let $ b $ be the unknown is the y-coordinate of point $ C (-1,b) $.
$ \quad \displaystyle \overline {AC}^2 = (2-(-1))^2+(3-b)^2 $
$ \quad \displaystyle \overline {AB}^2 = (2-(-3))^2+(3-4)^2 = 26 $
$ \quad \displaystyle \overline {BC}^2 = (-3-(-1))^2+(4-b)^2 $
Triangle $ABC$ is a right triangle with hypotenuse $ AC $ if and only if $ \overline {AC}^2 = \overline {AB}^2 + \overline {BC}^2 $, hence the equation
$ \quad \displaystyle (2-(-1))^2+(3-b)^2 = 26 + (-3-(-1))^2+(4-b)^2 $
$ \quad \displaystyle 2b = 28 $
$ \quad b = 14 $
The coordinates of point $ C $ so that $ ABC $ is a right triangle with hypotenuse $ AC $ are $ (-1,14) $
Solution
Linda spends $ 70\% $ of her monthly budget on housing and food and spends $ \$ 500 $ more on housing than on food. She spends $ 5\% $ of her budget, and that is $ \$ 200 $, to pay for a monthly membership at a yoga club.
How many dollars does she spend on food and how many dollars does she spend on housing separately ?

Let $ x $ be the budget in dollars. We are told that $ 5\% $ of her budget is $ \$ 200 $, hence the equation
$ \quad 5\% \cdot x = 200 $
Which may be written as
$ \quad \displaystyle \frac{5 x}{100} = 200 $
Solve for $ x $.
$ \quad x = 4000 $ dollars
Let $ h $ and $ f $ be the amount in dollars spent on housing and food respectively. We are told that $ 70\% $ of her monthly budget is on housing and food, hence the equation
$ \quad \displaystyle h + f = 70\% \cdot 4000 $
Which gives
$ \quad \displaystyle h + f = 2800 \qquad (I) $
We are told that Linda spends $ \$ 500 $ more on housing than on food, hence
$ \quad h = 500 + f \qquad (II) $
Solve equations (I) and (II) simultaneously to obtain
$ \quad h =1650 , f = 1150 $
Hence Linda spends $ \$ 1650 $ on housing and $ \$ 1150 $ on food.
Solution
Find the area of the kite shown below given that $ \overline {CD} = 10 $ cm.

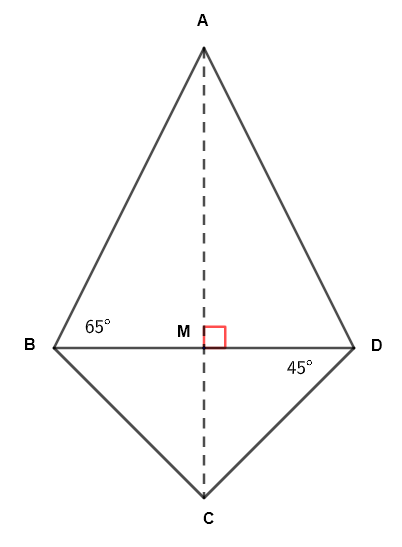
The area $ A_r $ of the given kite is given by
$ A_r = \frac{1}{2} \overline {AC} \cdot \overline {BD} $
We therefore need to find $ \overline {AC} $ and $ \overline {BD} $.
Since angle $ \angle MDC = 45^{\circ} $, $ \angle MCD = 90^{\circ} - 45^{\circ} = 45^{\circ} $ and hence triangle $ DMC $ is a right isosceles triangle, hence
$ \quad \overline {DM} = \overline {MC} $ (isosceles triangle)
$ \quad \overline {DC}^2 = \overline {DM}^2 + \overline {MC}^2 $ (Pythagorean theorem)
The above gives
$ \quad 10^2 = 2 \overline {DM}^2 $
Solve to obtain
$ \quad \displaystyle \overline {DM} = \frac{10}{\sqrt 2} $
Also, the kite is symmetric and therefore
$ \quad \displaystyle \overline {BM} = \overline {DM} = \frac{10}{\sqrt 2} $
which gives
\[ \quad \overline {BD} =\overline {BM} + \overline {DM} = \frac{10}{\sqrt 2} + \frac{10}{\sqrt 2} = 10 \sqrt 2\]

We now determine the height $ AM $ of triangle $ ABD $ using angle $ ABM $ whose size is given.
$ \quad \displaystyle \tan 65^{\circ} = \frac{\overline {AM}}{\overline {BM}} $
hence
$ \quad \displaystyle \overline {AM} = \overline {BM} \tan 65^{\circ} = \frac{10}{\sqrt 2} \tan 65^{\circ} $
$ \quad \displaystyle \overline {MC} = \overline {DM} = \frac{10}{\sqrt 2} $ (isosceles triangle)
\[ \quad \displaystyle \overline {AC} = \overline {AM} + \overline {MC} = \frac{10}{\sqrt 2} \tan 65^{\circ} + \frac{10}{\sqrt 2} \]
We now substitute in the formula $ A_r = \frac{1}{2} \overline {AC} \cdot \overline {BD} $ given above to obtain the area.

\[ \quad \displaystyle A_r = \frac{1}{2} \left(\frac{10}{\sqrt 2} \tan 65^{\circ} + \frac {10}{ \sqrt 2} \right) \cdot 10 \sqrt 2 = 157.23 \text{ unit squared} \].
Solution
m and n are parallel lines. Show that lines m and r are perpendicular.

Label different angles.

Lines m and n are parallel and line s intersects both of them creating corresponding angles .
Angles $ \alpha $ and $ \beta $ are corresponding angles and therefore have equal measures.
$ \quad \beta = \alpha = 33^{\circ} $
Angles $ \beta $ and $ \Omega $ are vertical angles and therefore have equal measures.
$ \quad \Omega = \beta = 33^{\circ} $
We now use the sum of the angles in triangle $ ABC $ to find the size of angle $ \theta $.
$ \quad 89 + 34 + \theta = 180 $
Hence
$ \quad \theta = 180 - 89 - 34 = 57^{\circ}$
The size of the angle made by lines r and m is equal to $ \theta + \Omega $
$ \quad \theta + \Omega = 57 + 33 = 90^{\circ}$
Lines r and m make an angle of $ 90^{\circ} $ and are therefore perpendicular.
Solution
Find the length of the height AM of the right square pyramid if its volume is 1500 cubic centimeters and the length of the diagonal CE of its base is equal to 10 centimeters.

Let the length of the square base be $ x $ and the length of the height AM be $ h $. The formula of the volume $ V $ of the pyramid is given by
$ \quad \displaystyle V = \frac{1}{3} x^2 h $
Let us consider the right triangle $ CDE $ whose sides have equal length $ x $ and the length of its hypotenuse $ CE $ is equal to 10.
Use the Pythagorean theorem
$ \quad x^2 + x^2 = 10^2 $
$ \quad 2 x^2 = 100 $
Solve for $ x^2 $
$ \displaystyle \quad x^2 = 50 $
We now substitute $ x^2 $ and the volume $ V $ by their values in the formula given above to write the equation
$ \quad \displaystyle 1500 = \frac{1}{3} 50 h $
Solve for $ h $
$ \quad h = 90 $ cm

Free Mathematics Tutorials

Solutions to Grade 10 Math Practice Test Questions

More References and links

Popular Pages

More Info

Stay In Touch

Navigation

Search