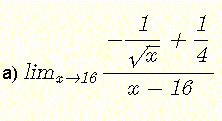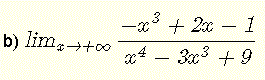Serangkaian pertanyaan Kalkulus 1 dengan solusi mendetail untuk berlatih menghadapi ujian, ujian, ujian penempatan, ... dan dapatkan pemahaman mendalam tentang topik berikut:

1. Fungsi
2. Batas
3. Kelanjutan
4. Turunan
5. Aplikasi Turunan

1. 
   Pertanyaan 1
   Temukan domain fungsi
2. 
   Pertanyaan 2
   Temukan jangkauan fungsi \( \)\( \)\( \)\( \)\( \)
3. 
   Pertanyaan 3
   Temukan invers dari fungsi \( f(x) = ln (2x - 3) + 2 \).
4. 
   Pertanyaan 4
   Evaluasi setiap limit berikut
   
   
   
   
   
   
   
   
   
5. 
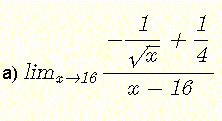
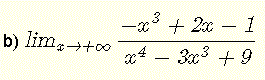
   Pertanyaan 5
   a) Grafik \( y = e^{x-1} \) dan \( y = x \) dalam sistem koordinat yang sama kemudian tunjukkan bahwa kedua grafik bersinggungan di titik \( (1,1) \) dan itu \( e^{x-1} \ge x \)
   b) Gunakan hasil yang diperoleh di bagian a) untuk menentukan kecekungan fungsi \( f(x) = \dfrac{x^3}{6} - e^{x-1} \) dan titik belok jika ada.
6. 
   Pertanyaan 6
   Carilah turunan dari fungsi-fungsi berikut dan jangan sederhanakan jawaban akhirnya.
   
   a) \( f(x) = e^{x-1} + \ln (3x-1) + \sin(2x+1) \)
   
   b) \( g(x) = (2x-1)^2(\tan(x)-1) \)
   
   c) \( h(x) = \dfrac{x - \cos(x)}{x^2-2x+1} \)
   
   d) \( m(x) = \sin \left(\sqrt{x^3 - \dfrac{1}{x} + 2} \right) \)
   
   e) \( n(x) = 3^{ 2x+3} + \log_3(2x-1) \)
7. 
   Pertanyaan 7
   Cari persamaan garis singgung kurva dengan persamaan \( \sin(y^2) = x^2 \) di titik \( ( 0,\sqrt{\pi}) \).
8. 
   Pertanyaan 8
   Temukan konstanta \( a \) dan \( b \) agar fungsi \( f \) kontinu pada \( (-\infty , +\infty ) \)
   \( f(x) = \left\{ \begin{array}{ll} 2x - 1 & x\le 1 \\ a x^3 + b & 1 \lt x \lt 2 \\ x + 2 b & x\ge 2 \\ \end{array} \right. \)
9. 
   Pertanyaan 9
   Tentukan persamaan garis singgung kurva dengan persamaan \( y = x + \sin(x) \) di \( x = 0 \).
10. 
    Pertanyaan 10
    Gunakan definisi turunan sebagai limit untuk mencari turunan \( f' \) di mana \( f(x) = \sqrt{x+2} \).
11. 
    Pertanyaan 11
    Tentukan pada interval berapa fungsi \( f(x) = e^x(x^2-5x+8)+\dfrac{x^4}{12}-\dfrac{x^3}{6 } \) cekung ke atas dan cekung ke bawah dan setiap titik belok.
12. 
    Pertanyaan 12
    Gunakan metode Newton dengan aproksimasi awal \( x_1 = 2 \) untuk mencari aproksimasi kedua dari solusi persamaan \( e^x = x^3 \).
13. 
    Pertanyaan 13
    Temukan maksimum dan minimum absolut dari fungsi \( f(x) = x^4 - x^3 \) pada interval \( [0,5] \).
14. 
    Pertanyaan 14
    Jika dimensi \( L \),\( W \) dan \( H\) dari sebuah kotak persegi panjang berubah dengan laju \( \dfrac{dL}{dt} = 0,1 \; cm/detik \), \( \dfrac{dW}{dt} = - 0,2 \; cm/detik\) dan \( \dfrac{dH}{dt} = 0,3 \; cm/detik\), berapa laju volume kotak berubah ketika \( L = 20 \; cm \), \( W = 8 \; cm \) dan \( H = 5 \; cm \)?
15. 
    Pertanyaan 15
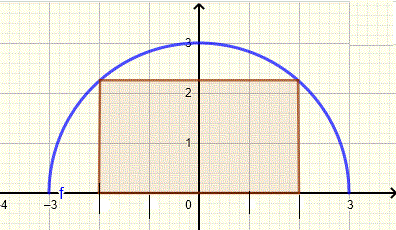
    Berapakah ukuran persegi panjang dengan luas terbesar yang dapat ditulisi setengah lingkaran dengan jari-jari 3?
    
    
    

Solusi Lengkap untuk Pertanyaan di Atas

1. 
   Solusi untuk Pertanyaan 1
   Agar fungsi \( f \) mengambil nilai riil, ekspresi di bawah akar di pembilang harus bukan negatif, dan ekspresi di bawah akar di penyebut harus positif; maka ketidaksetaraan untuk memecahkan
   \( x - 1 \ge 0 \) dan \( 4 - x^2 \gt 0 \)
   Himpunan penyelesaian untuk pertidaksamaan pertama dan kedua adalah berturut-turut
   \( x \ge 1 \) dan \( -2 \lt x \lt 2 \)
   Kedua pertidaksamaan harus dipenuhi secara bersamaan, oleh karena itu domain dari fungsi yang diberikan adalah perpotongan dari himpunan \( x \ ge 1 \) dan \( -2 \lt x \lt 2 \) yang diberikan oleh
   \( 1 \le x \lt 2 \)
   
   
2. 
   Solusi untuk Pertanyaan 2
   Menurut properti fungsi invers, salah satu cara untuk menemukan rentang dari fungsi yang diberikan adalah mencari domain inversnya.
   Mari kita buktikan dulu bahwa \( f \) adalah fungsi satu ke satu dan kemudian temukan terbalik. Untuk membuktikan bahwa \( f \) adalah fungsi satu ke satu dan karenanya dapat dibalik, kami menggunakan kontrapositif dari fungsi satu ke satu dan mulai dengan \( f(a) = f(b) \) dan buktikan bahwa \( a = b \). Karena itu
   \( \dfrac{a - 1}{2-3 a} = \dfrac{b - 1}{2-3 b} \)
   Kalikan silang
   \( (a - 1)(2-3 b) = (2 - 3 a)(b - 1) \)
   Memperluas
   \( 2a - 2 - 3 ab + 3 b = 2 b - 2 - 3 ab + 3 a \)
   Kelompokkan istilah-istilah yang disukai
   \( 2 a = 2 b \)
   Selesaikan untuk a
   \(a = b\)
   yang membuktikan bahwa fungsi \( f \) adalah fungsi satu ke satu dan karenanya memiliki invers
   Invers dari \( f \) dapat dihitung dimulai dengan persamaan
   \( y = \dfrac{x - 1}{2-3x} \)
   Kalikan silang persamaan di atas
   \( 2 y - 3 x y = x - 1 \)
   dan selesaikan untuk \( x \)
   \( x = \dfrac{2 y + 1}{3y + 1} \)
   Tukarkan \( x \) dan \( y \) pada persamaan di atas untuk mendapatkan invers \( f^{-1} \)
   \( f^{-1}(x) = y = \dfrac{2 x + 1 }{3x + 1} \).
   Domian \( f^{-1} \) adalah himpunan semua bilangan real kecuali \( -\dfrac{1}{3} \). Oleh karena itu, jangkauan \( f \) adalah himpunan semua bilangan real kecuali \( -\dfrac{1}{3} \) yang dapat ditulis dalam bentuk interval sebagai
   \( (-\infty , - \dfrac{1}{3}) \cup (- \dfrac{1}{3} , +\infty) \)
   
   
3. 
   Solusi untuk Pertanyaan 3
   Tulis fungsi sebagai persamaan sebagai berikut
   \( y = ln (2x - 3) + 2 \)
   Selesaikan soal di atas untuk x
   \( y - 2 = ln (2x - 3) \)
   \( 2x - 3 = e^{y - 2} \)
   \( 2 x = e^{y - 2} + 3 \)
   \( x = \dfrac{1}{2} (e^{y - 2} + 3) \)
   Pertukaran \( x \) dan \( y \)
   \( y = \dfrac{1}{2} (e^{x - 2} + 3) \)
   Invers dari \( f \) diberikan oleh
   \( f^{-1}(x) = \dfrac{1}{2} (e^{x - 2} + 3) \)
   
   
4. 
   Solusi untuk Pertanyaan 4
   A)
   Batas berbentuk tak tentu \( \dfrac{0}{0} \).
   Kalikan pembilang dan penyebut dengan konjugasi pembilangnya \( -\dfrac{1}{\sqrt x} - \dfrac{1}{4} \)
   
   \( \lim_{x\to 16} \dfrac{-\dfrac{1}{\sqrt x} + \dfrac{1}{4}}{x - 16 } \) = \( \lim_{x\to 16} \dfrac{ (-\dfrac{1}{\sqrt x} + \dfrac{1}{4})(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } { (x - 16)(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } \)
   Menyederhanakan
   \( = \lim_{x\to 16} \dfrac{ \dfrac{1}{x} - \dfrac{1}{16} }{ (x - 16)(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } = \lim_{x\to 16} \dfrac{ \dfrac{16-x}{16x} }{ (x - 16)(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } \)
   
   \( = \lim_{x\to 16} \dfrac{-1}{16x(-\dfrac{1}{\sqrt x} - \dfrac{1}{4})} = \dfrac{-1}{ 16 \times 16(-\dfrac{1}{\sqrt 16} - \dfrac{1}{4})} = \dfrac{1}{128}\)
   
   B)
   Limitnya berbentuk tak tentu \( \dfrac{\infty}{\infty} \).
   Bagilah semua suku di pembilang dan semua suku penyebut dengan pangkat tertinggi yang ada di \( x^4 \)
   \( \lim_{x\to +\infty} \dfrac{-x^3+2x-1}{x^4 - 3 x^3 + 9 } = \lim_{x\to +\infty} \dfrac{ \dfrac{-x^3}{x^4}+\dfrac{2x}{x^4}-\dfrac{1}{x^4}}{\dfrac{x^4}{x^4} - \dfrac{3 x^3}{x^4} + \dfrac{9}{x^4} }\).
   Sederhanakan suku-suku rasional
   \( = \lim_{x\to +\infty} \dfrac{\dfrac{-1}{x}+\dfrac{2}{x^3}-\dfrac{1}{x^4}}{1 - \dfrac{3}{x} + \dfrac{9}{x^4} } = \dfrac{0+0-0}{1 - 0 + 0 } = \dfrac{0}{1} = 0\)
   
   C)
   Batasnya berbentuk tak tentu \( \infty \cdot 0 \).
   Misalkan \( t = \dfrac{3}{x} \) dan tulis ulang limit dalam bentuk t.
   \( \lim_{x\to +\infty} x \sin(\dfrac{3}{x}) = \lim_{t\to 0} 3 \dfrac {\sin(t)}{t} \).
   Menggunakan hasil yang terkenal \( \lim_{t\to 0} \dfrac {\sin(t)}{t} = 1 \), limit dievaluasi menjadi
   \( = 3 \times 1 = 3\)
   
   D)
   \( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \dfrac{0}{0}\), bentuk tak tentu
   Gunakan Aturan L'Hospital ke bentuk tak tentu, kita dapat menulis
   \( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \lim_{x\to 0} \dfrac{ d (\sin(x)+x) / dx }{ d(2x^2+x)/dx} = \lim_{x\to 0} \dfrac{ cos(x)+ 1 }{ 4x+1} = \dfrac{ cos(0)+ 1 } { 4\times 0+1} = 2\)
   
   e)
   \( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} \).
   Diketahui bahwa kisaran \( \sin(x) \) diberikan oleh
   \( -1 \le \sin(x) \le 1 \)
   Tambahkan 1 ke semua suku pertidaksamaan untuk mendapatkan pertidaksamaan berikut
   \( -1 + 1 \le \sin(x) + 1 \le 1 + 1 \)
   \( 0 \le \sin(x) + 1 \le 2 \)
   Bagilah semua suku dari pertidaksamaan di atas dengan positif \( x \)
   \( \dfrac{0}{x} \le \dfrac{\sin(x) + 1}{x} \le \dfrac{2}{x} \)
   Kita memiliki \( \lim_{x\to +\infty} \dfrac{0}{x} = 0 \) dan \( \lim_{x\to +\infty} \dfrac{2}{x} = 0 \)
   Dengan menggunakan teorema squeezing (atau Sandwich) , kita dapat mengevaluasi limit yang diberikan sebagai berikut
   \( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} = 0 \)
   
   
5. 
   Solusi untuk Pertanyaan 5
   A)
   Grafik dari \( y = e^{x-1} \) dan \( y = x \) ditunjukkan di bawah ini. turunan dari \( y = e^{x-1} \) sama dengan \( y ' = e^{x-1} \) dan kemiringan \( m \) garis singgung di \( x = 1 \) adalah nilai turunan di \( x = 1\). Karena itu
   
   
   \( m = e^{1-1}= 1 \)
   Persamaan garis singgung di titik \( (1,1) \) diberikan oleh
   \( y - 1 = 1 \times (x - 1) \)
   Yang menyederhanakan untuk
   \( y = x \)
   Oleh karena itu grafik dari \( y = e^{x-1} \) dan \( y = x \) bersinggungan dengan titik \( (1,1) \) dan oleh karena itu kita dapat menyatakan secara grafis bahwa \( e^ {x-1} \ge x \).
   B)
   Turunan pertama dan kedua dari \( f \) diberikan oleh
   \( f'(x) = \dfrac{x^2}{2}-e^{x-1} \)
   \( f''(x) = x-e^{x-1} \)
   titik belok terjadi pada nilai \( x \) di mana \( f''(x ) \) ganti tanda. Kita telah melihat di bagian a) bahwa \( e^{x-1} \ge x \) yang dapat ditulis sebagai
   \( x-e^{x-1} \le 0 \)
   dan karena itu \( f''(x) \) negatif dan memiliki nol di \( x = 1 \). Oleh karena itu grafik \( f(x) \) cekung ke bawah dan tidak memiliki titik belok karena \( f''(x) \) tidak berubah tanda.
   
   
6. 
   Solusi untuk Pertanyaan 6
   a) Jumlahkan aturan turunan menghasilkan: \( f'(x) = e^{x-1 } + \dfrac{3}{3x-1} + 2 \cos(2x+1) \)
   b) Aturan perkalian turunan: \( g'(x) = 4(2x-1)(\tan(x)-1) + (2x-1)^2(\sec^2(x)) \)
   c) aturan hasil bagi turunan: \( h'(x) = \dfrac{ (1 + \sin(x))(x^2-2x+1) - (x - \cos(x))(2x-2 ) }{(x^2-2x+1)^2} \)
   
   d) Biarkan \( u = \sqrt{x^3 - \dfrac{1}{x} + 2} \) , tulis fungsi \(m \) sebagai \(m = \sin u \) lalu gunakan aturan rantai turunan
   
   \( m'(x) = \dfrac{d m}{d u} \dfrac{d u}{d x} = \cos(u) \dfrac{1}{2}(3x^2+\dfrac{1}{x ^2})(x^3 - \dfrac{1}{x} + 2)^{-1/2} \)
   
   \( = \dfrac{1}{2} \cos \left(\sqrt{x^3 - \dfrac{1}{x} + 2} \right) (3x^2+\dfrac{1}{x^ 2})(x^3 - \dfrac{1}{x} + 2)^{-1/2} \)
   
   e)
   Tulis ulang \( 3^{ 2x+3} \) dan \( \log_3(2x-1) \) sebagai
   \( 3^{2x+3} = e^{(2x+3) \ln 3}\) , perubahan basis eksponensial
   \( \log_3(2x-1) = \dfrac{ \ln(2x-1)}{ \ln 3}\) , perubahan basis logaritma
   Gantikan dan tulis ulang \( n(x) \) sebagai
   \( n(x) = 3^{ 2x+3} + \log_3(2x-1) = e^{(2x+3) \ln 3} + \dfrac{ \ln(2x-1)}{ \ln 3} \)
   Kami sekarang menghitung turunannya
   \( n'(x) = ( 2 \ln 3 ) e^{(2x+3) \ln 3} + \dfrac{1}{ \ln 3} \dfrac{2}{2x-1} = ( 2 \ln 3 ) 3^{2x+3} + \dfrac{2}{\ln 3(2x-1)} \)
   
   
7. 
   Solusi untuk Pertanyaan 7
   Kami pertama-tama membedakan persamaan yang diberikan secara implisit
   \( 2 y \dfrac{d y}{d x} cos(y^2) = 2 x \)
   \( \dfrac{d y}{d x} = \dfrac{ x}{ y cos(y^2)} \)
   Kemiringan \( m \) garis singgung diberikan oleh nilai \( \dfrac{d y}{d x} \) pada titik \( ( 0,\sqrt{\pi}) \).
   \( m = \dfrac{(0)}{\sqrt{\pi} cos((\sqrt{{\pi}})^2)} = 0 \)
   Persamaan, dalam bentuk kemiringan titik, dari garis singgung ke kurva di titik \( ( 0,\sqrt{\pi}) \) diberikan oleh
   \( y - \sqrt{\pi} = 0(x - 0) \)
   Ini adalah garis horizontal yang diberikan oleh
   \( y = \sqrt{\pi} \)
   
   
8. 
   Solusi untuk Pertanyaan 8
   \( f(x) \) adalah kontinu pada interval \( (-\infty , 1) \) , \( (1,2) \) dan \( (2 , +\infty) \). Kita perlu menemukan \( a \) dan \( b \) sehingga juga kontinu di \( x = 1 \) dan \( x = 2 \) dan karenanya kontinu di \( (-\infty , +\infty ) \).
   \( f(1) = 1 \)
   \( \lim_{x\to 1^-} f(x) = 1 \)
   \( \lim_{x\to 1^+} f(x) = a(1)^3+b = a + b \)
   Batas dari kiri dan kanan \( 1 \) harus sama
   \( a + b = 1 \) (persamaan 1)
   \( f(2) = 2 + 2 b \)
   \( \lim_{x\to 2^-} f(x) = a(2)^3 + b = 8 a + b \)
   \( \lim_{x\to 2^+} f(x) = 2 + 2 b \)
   Batas dari kiri dan kanan \( 2 \) harus sama
   \( 8 a + b = 2 + 2 b \) (persamaan 2)
   Selesaikan persamaan (1) dan (2) secara bersamaan untuk menemukan
   \( a = \dfrac{1}{3} \) dan \( b = \dfrac{2}{3} \)
   
   
9. 
   Solusi untuk Pertanyaan 9
   Temukan turunan dari \( y \).
   \( y' = 1 + \cos(x) \)
   Kemiringan \( m \) garis singgung di \( x = 0 \) sama dengan nilai \( y' \) di \( x = 0 \). Karena itu
   \(m = 1 + \cos(0) = 2 \)
   Koordinat y dari titik singgung \( P \) diberikan oleh nilai \( y \) di \( x = 0 \). Karena itu
   \( P(0 , 0 + \sin(0)) = P(0,0) \)
   Persamaan garis singgung dalam bentuk kemiringan titik diberikan oleh
   \( y - 0 = 2(x - 0) \)
   dan dalam bentuk perpotongan lereng
   \( y = 2 x \)
   
   
10. 
    Solusi untuk Pertanyaan 10
    Definisi turunan \( f' \) dari fungsi \( f \) diberikan oleh limit
    \( f'(x) = \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \)
    Gantikan \( f(x) \) dengan \( \sqrt{x+2} \) pada definisi di atas untuk mendapatkan
    \( f'(x) = \lim_{h\to 0} \dfrac{\sqrt{x + h +2}- \sqrt{x+2} }{h} \)
    Batas di atas berbentuk tak tentu \( \dfrac{0}{0} \). Kalikan pembilang dan penyebutnya dengan konjugat pembilangnya
    \( f'(x) = \lim_{h\to 0} \dfrac{ (\sqrt{x + h +2}- \sqrt{x+2} ) (\sqrt{x + h +2} + \ sqrt{x+2} ) }{h(\sqrt{x + h +2} + \sqrt{x+2} )} \)
    Perluas pembilang dan sederhanakan
    \( f'(x) = \lim_{h\to 0} \dfrac{ (x + h + 2)- (x + 2) ) }{h(\sqrt{x + h +2} + \sqrt{ x+2} )} = \lim_{h\to 0} \dfrac{ h }{h(\sqrt{x + h +2} + \sqrt{x+2} )}\)
    Bagi pembilang dan penyebut dengan \( h \) (atau batalkan \( h \))
    \( f'(x) = \lim_{h\to 0} \dfrac{ 1 }{\sqrt{x + h +2} + \sqrt{x+2} }\)
    Evaluasi limit dan turunannya
    \( f'(x) = \dfrac{ 1 }{ \sqrt{x + 0 + 2} + \sqrt{x + 2} } = \dfrac{ 1 }{2 \sqrt{x + 2} }\)
    
    
    
11. 
    Solusi untuk Pertanyaan 11
    Temukan turunan pertama dan kedua
    \( f'(x) = e^x (x^2-5x+8) + e^x (2 x -5) +\dfrac{x^3}{3}-\dfrac{x^2}{ 2} = e^x (x^2-3x+3)+\dfrac{x^3}{3}-\dfrac{x^2}{2} \)
    \( f''(x) = e^x(x^2-3x+3)+e^x(2x-3) + x^2-x = e^x(x^2-x)+x^ 2-x = x (x - 1) e^x \)
    \( f'' \) memiliki dua nol: \( x = 0 \) dan \( x = 1\) dan \( e^x \) selalu positif. Oleh karena itu tabel tanda \( f'' \) memiliki tiga interval
    1) \( (-\infty , 0 ) \) , nilai tes \( x = -1 \) , \( f''(-1) = 2/e \) , maka \( f''(x) \) positif pada interval \( (-\infty , 0 ) \).
    2) \( (0 , 1 ) \) , nilai tes \( x = 1/2 \) , \( f''(1/2) = -\dfrac{\sqrt 2}{4} \) , maka \( f''(x) \) negatif pada interval \( (0 , 1 ) \).
    3) \( (1 , +\infty ) \) , nilai tes \( x = 2 \) , \( f''(2) = 2e^2 \) , \( f''(x) \) adalah positif pada interval \( (1 , +\infty ) \).
    \( f'' \) adalah cekung pada interval \( (-\infty , 0 ) \) dan \( (1 , +\infty ) \) , dan cekung ke bawah pada interval \( (0 , 1 ) \).
    \( f'' \) berubah tanda di \( x = 0 \) dan \( x = 1 \) dan karenanya memiliki titik belok di \( x = 0 \) dan \( x = 1 \).
    
    
    
12. 
    Solusi untuk Pertanyaan 12
    metode Newton didasarkan pada algoritme berikut: mengetahui perkiraan \( x_n \) untuk solusi dari suatu persamaan \( f(x) = 0 \), pendekatan berikutnya \( x_{n+1}\) ke persamaan diberikan oleh
    \( x_{n+1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \).
    Solusi dari persamaan yang diberikan \( e^x = x^3 \) sama dengan solusi dari persamaan \( f(x) = e^x - x^3 = 0 \)
    \( f'(x) = e^x - 3x^2 \)
    Kita tahu perkiraan pertama \( x_1 = 2 \); menggunakan algoritma Newton kami memperkirakan \( x_2\) dengan
    \( x_{2} = x_1 - \dfrac{f(x_1)}{f'(x_1)} = 2 - \dfrac{e^2 - 2^3}{e^2 - 3 \times 2^2} \approx 1,87 \) (dibulatkan menjadi dua tempat desimal)
    Perkiraan \(x_3\) dapat diperoleh dengan menggunakan \( x_2 \) ditemukan di atas dan seterusnya.
    
    
    
13. 
    Solusi untuk Pertanyaan 13
    Temukan turunan pertama dan faktorkan.
    \( f'(x) = 4 x^3 - 3 x^2 = x^2(4x - 3)\)
    \( f'(x) \) memiliki dua nol pada \( x = 0 \) dan \( x = 3/4 \) dan keduanya berada dalam interval \( [0,5] \). Nol dari \( f'(x) \) disebut titik kritis.
    Kita sekarang mengevaluasi fungsi pada titik akhir interval yang diberikan dan nol dari \( f'(x) \).
    \( f(0) = 0 \)
    \( f(5) = 5^4 - 5^3 = 500 \)
    \( f(3/4) = (3/4)^4 - (3/4)^3 = -\dfrac{27}{256} \)
    Membandingkan nilai-nilai ini, \( f(x) \) memiliki maksimum absolut sama dengan \(500 \) pada titik akhir \( x = 5 \) dan minimum absolut sama dengan \( -\dfrac{27}{256} \) pada titik kritis \( x = 3/4 \)
    Lebih banyak pertanyaan tentang minimum absolut dan maksimum fungsi disertakan.
    
    
14. 
    Solusi untuk Pertanyaan 14
    Volume \( V \) kotak persegi panjang dengan dimensi \( L \),\( W \) dan \( H\) diberikan oleh
    \( V = L(t) W(t) H(t) \)
    di mana \( L(t)\) , \( W(t) \) dan \( H(t) \) adalah fungsi waktu \( t \).
    Karena dimensi kotak berubah terhadap waktu, volume kotak juga berubah terhadap waktu pada tingkat perubahan dari \( V\) diberikan oleh turunan pertama \( \dfrac{dV}{dt} \).
    \( \dfrac{dV}{dt} = W(t) H(t) \dfrac{d L}{dt } + L(t) H(t) \dfrac{d W}{dt } + L(t ) W(t) \dfrac{d H}{dt } \)
    Substitusikan besaran yang diketahui dengan nilai numeriknya
    \( \dfrac{dV}{dt} = 8 \times 5 \times 0,1 + 20 \times 5 \times (-0,2) + 20 \times 8 \times 0,3 = 32 \; cm^3 / detik \)
    
    
    
15. 
    Solusi untuk Pertanyaan 15
    Persamaan lingkaran dengan jari-jari \( 3 \) dan berpusat di \( (0 , 0) \)diberikan oleh
    \( x^2 + y^2 = 3^2 \)
    Selesaikan persamaan di atas untuk y
    \(y^2 = 9 - x^2\)
    \( y = \pm \sqrt{9 - x^2} \)
    Persamaan setengah lingkaran atas adalah \( y = \sqrt(9-x^2) \)
    Sebuah titik pada setengah lingkaran dengan koordinat x \( x \) memiliki koordinat y sama dengan \(\sqrt{9 - x^2} \) (lihat grafik di bawah)
    Persegi panjang memiliki panjang \( L = 2x \) dan lebar (atau tinggi) \( W = \sqrt(9-x^2) \). Luas \( A \) persegi panjang diberikan oleh
    \( A(x) = L \times W = 2 x \sqrt(9-x^2) \) , \( 0 \le x \le 3 \)
    
    Temukan turunan pertama dari \( A \)
    \( \dfrac{d A}{dx} = 2\sqrt{9-x^2} + (2x) (\dfrac{1}{2}) (-2x) (9-x^2)^{- 1/2} =\dfrac{2\left(-2x^2+9\right)}{\sqrt{9-x^2}} \)
    Nol dari \( \dfrac{d A}{dx} \) diberikan oleh nol dari pembilang \( \dfrac{d A}{dx} \)
    \( -2x^2+9 = 0 \)
    Memberikan dua nol: \( x = \sqrt{4,5} \) dan \( x = - \sqrt{4,5} \)
    Kami menganggap nol pada \( x = \sqrt{4.5} \) karena berada dalam interval \( [0 , 3 ] \)
    Kita sekarang mengevaluasi luas \( A(x) \) pada titik ujung \( x = 0 \) dan \( x = 3 \) dan pada titik kritis \( x = \sqrt{4,5} \).
    \( A(0) = 0 \)
    \( A(3) = 0 \)
    \( A(\sqrt{4.5}) = 9 \)
    Luas maksimum A adalah untuk \( x = \sqrt{4,5} \)
    Dimensinya adalah:
    \( L = 2 x = 2 \sqrt{4,5} \approx 4,24 \)
    \( W = \sqrt(9-x^2) = \sqrt(9-\sqrt{4,5}^2) \approx 2,12 \)
    Lebih banyak masalah pengoptimalan disertakan.

Referensi dan Tautan Lainnya