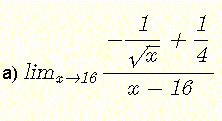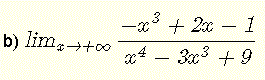Una serie di domande di Calcolo 1 con le relative soluzioni dettagliate per esercitarsi per test, esami, esami di collocamento... e acquisire una comprensione approfondita dei seguenti argomenti:
Funzioni
Limiti
Continuità
Derivati
Applicazioni di derivati
Le domande sono state progettate per coprire gli argomenti più importanti nel calcolo 1 e le loro soluzioni dettagliate includono collegamenti a più pratica in questi argomenti.
Domanda 1
Calcola il dominio della funzione
Domanda 2
Calcolare l'intervallo della funzione
\( \)\( \)\( \)\( \)\( \)
Domanda 3
Trova l'inverso della funzione \( f(x) = ln (2x - 3) + 2 \).
Domanda 4
Valuta ciascuno dei seguenti limiti
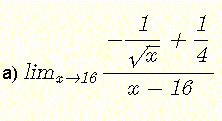
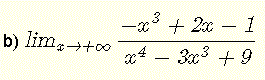
Domanda 5
a) Disegna \( y = e^{x-1} \) e \( y = x \) nello stesso sistema di coordinate e poi mostra che i due grafici sono tangenti nel punto \( (1,1) \ ) e che \( e^{x-1} \ge x \)
b) Utilizzare il risultato ottenuto nella parte a) per determinare la concavità della funzione \( f(x) = \dfrac{x^3}{6} - e^{x-1} \) e gli eventuali punti di flesso.
Domanda 6
Trova la derivata delle seguenti funzioni e non semplificare la risposta finale.
Domanda 7
Trova l'equazione della retta tangente alla curva con l'equazione \( \sin(y^2) = x^2 \) nel punto \( ( 0,\sqrt{\pi}) \).
Domanda 8
Trova le costanti \( a \) e \( b \) in modo che la funzione \( f \) sia continua su \( (-\infty , +\infty ) \)
\( f(x) = \left\{
\begin{array}{ll}
2x - 1 & x\le 1 \\
a x^3 + b & 1 \lt x \lt 2 \\
x + 2 b & x\ge 2 \\
\end{array}
\right. \)
Domanda 9
Trova l'equazione della retta tangente alla curva con l'equazione \( y = x + \sin(x) \) in \( x = 0 \).
Domanda 10
Usa la definizione della derivata come limite per trovare la derivata \( f' \) dove \( f(x) = \sqrt{x+2} \).
Domanda 11
Determina su quale/i intervallo/i è la funzione \( f(x) = e^x(x^2-5x+8)+\dfrac{x^4}{12}-\dfrac{x^3}{6 } \) concava verso l'alto e concava verso il basso e qualsiasi punto di flesso.
Domanda 12
Utilizzare il metodo di Newton con approssimazione iniziale \( x_1 = 2 \) per trovare una seconda approssimazione alla soluzione dell'equazione \( e^x = x^3 \).
Domanda 13
Trova il massimo e il minimo assoluti della funzione \( f(x) = x^4 - x^3 \) sull'intervallo \( [0,5] \).
Domanda 14
Se le dimensioni \( L \),\( W \) e \( H\) di una scatola rettangolare cambiano alla velocità \( \dfrac{dL}{dt} = 0.1 \; cm/sec \), \ ( \dfrac{dW}{dt} = - 0.2 \; cm/sec\) e \( \dfrac{dH}{dt} = 0.3 \; cm/sec\), a quale velocità è il volume della scatola
cambiando quando \( L = 20 \; cm \), \( W = 8 \; cm \) e \( H = 5 \; cm \)?
Domanda 15
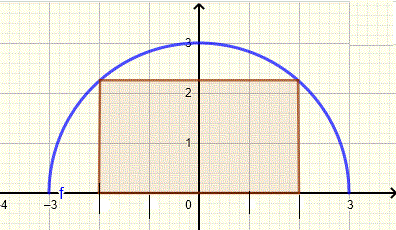
Quali sono le dimensioni del rettangolo di area maggiore inscrivibile in un semicerchio di raggio 3?
Soluzioni dettagliate alle domande di cui sopra
Soluzione alla domanda 1
Affinché la funzione \( f \) assuma valori reali, l'espressione sotto il radicale al numeratore deve essere non negativa e l'espressione sotto il radicale al denominatore deve essere positiva; da qui le disuguaglianze da risolvere
\( x - 1 \ge 0 \) e \( 4 - x^2 \gt 0 \)
Gli insiemi di soluzioni per la prima e la seconda disuguaglianza sono rispettivamente
\( x \ge 1 \) e \( -2 \lt x \lt 2 \)
Entrambe le disuguaglianze devono essere soddisfatte simultaneamente, quindi il dominio della funzione data è l'intersezione degli insiemi \( x \ ge 1 \) e \( -2 \lt x \lt 2 \) che è dato da
\( 1 \le x \lt 2 \)
Soluzione alla domanda 2
Secondo le proprietà delle funzioni inverse, un modo per trovare le intervallo della funzione data è trovare il dominio della sua inversa.
Proviamo prima che \( f \) è una funzione uno a uno e poi troviamo la sua inverso. Per dimostrare che \( f \) è una funzione uno a uno e quindi invertibile, usiamo il contropositivo della funzione uno a uno e iniziamo con
\( f(a) = f(b) \) e prova che \( a = b \). Quindi
\( \dfrac{a - 1}{2-3 a} = \dfrac{b - 1}{2-3 b} \)
Moltiplicazione incrociata
\( (a - 1)(2-3 b) = (2 - 3 a)(b - 1) \)
Espandere
\( 2a - 2 - 3 a b + 3 b = 2 b - 2 - 3 ab + 3 a \)
Raggruppa come termini
\( 2a = 2b\)
Risolvi per a
\(a = b\)
il che dimostra che la funzione \( f \) è una funzione uno a uno e quindi ha un'inversa
L'inverso di \( f \) può essere calcolato partendo dall'equazione
\( y = \dfrac{x - 1}{2-3x} \)
Moltiplicazione incrociata dell'equazione precedente
\( 2 y - 3 x y = x - 1 \)
e risolvi per \( x \)
\( x = \dfrac{2 y + 1}{3y + 1} \)
Scambia \( x \) e \( y \) nell'equazione precedente per ottenere l'inverso \( f^{-1} \)
\( f^{-1}(x) = y = \dfrac{2 x + 1 }{3x + 1} \).
La domiana di \( f^{-1} \) è l'insieme di tutti i numeri reali tranne \( -\dfrac{1}{3} \). Quindi l'intervallo di \( f \) è l'insieme di tutti i numeri reali tranne \( -\dfrac{1}{3} \) che può essere scritto in forma di intervallo come
\( (-\infty , - \dfrac{1}{3}) \cup (- \dfrac{1}{3} , +\infty) \)
Soluzione alla domanda 3
Scrivi la funzione come equazione come segue
\( y = ln (2x - 3) + 2 \)
Risolvi quanto sopra per x
\(y - 2 = ln (2x - 3) \)
\( 2x - 3 = e^{y - 2} \)
\( 2 x = e^{y - 2} + 3 \)
\( x = \dfrac{1}{2} (e^{y - 2} + 3) \)
Interscambio \( x \) e \( y \)
\( y = \dfrac{1}{2} (e^{x - 2} + 3) \)
L'inverso di \( f \) è dato da
\( f^{-1}(x) = \dfrac{1}{2} (e^{x - 2} + 3) \)
Soluzione alla domanda 4
a)
Il limite è nella forma indeterminata \( \dfrac{0}{0} \).
Moltiplica numeratore e denominatore per il coniugato del numeratore \( -\dfrac{1}{\sqrt x} - \dfrac{1}{4} \)
b)
Il limite è della forma indeterminata \( \dfrac{\infty}{\infty} \).
Dividi tutti i termini al numeratore e tutti i termini al denominatore per con il termine con la massima potenza che in \( x^4 \)
\( \lim_{x\to +\infty} \dfrac{-x^3+2x-1}{x^4 - 3 x^3 + 9 } = \lim_{x\to +\infty} \dfrac{ \dfrac{-x^3}{x^4}+\dfrac{2x}{x^4}-\dfrac{1}{x^4}}{\dfrac{x^4}{x^4} - \dfrac{3 x^3}{x^4} + \dfrac{9}{x^4} }\).
Semplifica i termini razionali
\( = \lim_{x\to +\infty} \dfrac{\dfrac{-1}{x}+\dfrac{2}{x^3}-\dfrac{1}{x^4}}{1 - \dfrac{3}{x} + \dfrac{9}{x^4} } = \dfrac{0+0-0}{1 - 0 + 0 } = \dfrac{0}{1} = 0\)
c)
Il limite è della forma indeterminata \( \infty \cdot 0 \).
Sia \( t = \dfrac{3}{x} \) e riscriviamo il limite in termini di t.
\( \lim_{x\to +\infty} x \sin(\dfrac{3}{x}) = \lim_{t\to 0} 3 \dfrac {\sin(t)}{t} \).
Usando il noto risultato \( \lim_{t\to 0} \dfrac {\sin(t)}{t} = 1 \), il limite vale
\( = 3 × 1 = 3\)
d)
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \dfrac{0}{0}\), forma indeterminata
Usa la Regola di L'Hospital nella forma indeterminata, possiamo scrivere
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \lim_{x\to 0} \dfrac{ d (\sin(x)+x) / dx }{ d(2x^2+x)/dx} = \lim_{x\to 0} \dfrac{ cos(x)+ 1 }{ 4x+1} = \dfrac{ cos(0)+ 1 } { 4× 0+1} = 2\)
e)
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} \).
È ben noto che l'intervallo di \( \sin(x) \) è dato da
\( -1 \le \sin(x) \le 1 \)
Aggiungi 1 a tutti i termini della disuguaglianza per ottenere la seguente disuguaglianza
\( -1 + 1 \le \sin(x) + 1 \le 1 + 1 \)
\( 0 \le \sin(x) + 1 \le 2 \)
Dividi tutti i termini della disuguaglianza di cui sopra per \( x \) positivo
\( \dfrac{0}{x} \le \dfrac{\sin(x) + 1}{x} \le \dfrac{2}{x} \)
Abbiamo \( \lim_{x\to +\infty} \dfrac{0}{x} = 0 \) e \( \lim_{x\to +\infty} \dfrac{2}{x} = 0 \ )
Utilizzando il teorema della squeezing (o Sandwich) , possiamo valutare il limite dato come segue
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} = 0 \)
Soluzione alla domanda 5
a)
Il grafico di \( y = e^{x-1} \) e \( y = x \) è mostrato sotto. La derivata di \( y = e^{x-1} \) è uguale a \( y ' = e^{x-1} \) e la pendenza \( m \) della tangente in \( x = 1 \) è il valore della derivata in \( x = 1\). Quindi
\( m = e^{1-1}= 1 \)
L'equazione della retta tangente nel punto \( (1,1) \) è data da
\( y - 1 = 1 \times (x - 1) \)
Il che semplifica a
\(y = x\)
Quindi i grafici di \( y = e^{x-1} \) e \( y = x \) sono tangenti nel punto \( (1,1) \) e possiamo quindi affermare graficamente che \( e^ {x-1} \ge x \).
b)
Le derivate prima e seconda di \( f \) sono date da
\( f'(x) = \dfrac{x^2}{2}-e^{x-1} \)
\( f''(x) = x-e^{x-1} \)
Un punto di flesso si verifica a un valore di \( x \) dove \( f''(x ) \) cambia segno. Abbiamo visto nella parte a) che \( e^{x-1} \ge x \) che può essere scritto come
\( x-e^{x-1} \le 0 \)
e quindi \( f''(x) \) è negativo e ha uno zero in \( x = 1 \). Quindi il grafico di \( f(x) \) è concavo verso il basso e non ha un punto di flesso perché \( f''(x) \) non cambia segno.
Soluzione alla domanda 6
a) La regola della somma delle derivate dà: \( f'(x) = e^{x-1 } + \dfrac{3}{3x-1} + 2 \cos(2x+1) \)
b) Regola del prodotto delle derivate: \( g'(x) = 4(2x-1)(\tan(x)-1) + (2x-1)^2(\sec^2(x)) \)
c) regola del quoziente delle derivate: \( h'(x) = \dfrac{ (1 + \sin(x))(x^2-2x+1) - (x - \cos(x))(2x-2 ) }{(x^2-2x+1)^2} \)
d) Sia \( u = \sqrt{x^3 - \dfrac{1}{x} + 2} \) , scrivi la funzione \(m \) come \(m = \sin u \) quindi usa regola della catena delle derivate
e)
Riscrivi \( 3^{ 2x+3} \) e \( \log_3(2x-1) \) come
\( 3^{2x+3} = e^{(2x+3) \ln 3}\) , cambio di base degli esponenziali
\( \log_3(2x-1) = \dfrac{ \ln(2x-1)}{ \ln 3}\) , cambio di base dei logaritmi
Sostituisci e riscrivi \( n(x) \) come
\( n(x) = 3^{ 2x+3} + \log_3(2x-1) = e^{(2x+3) \ln 3} + \dfrac{ \ln(2x-1)}{ \ln 3} \)
Calcoliamo ora la derivata
\( n'(x) = ( 2 \ln 3 ) e^{(2x+3) \ln 3} + \dfrac{1}{ \ln 3} \dfrac{2}{2x-1} = ( 2 \ln 3 ) 3^{2x+3} + \dfrac{2}{\ln 3(2x-1)} \)
Soluzione alla domanda 7
Prima distinguiamo l'equazione data implicitamente
\( 2 y \dfrac{d y}{d x} cos(y^2) = 2 x \)
\( \dfrac{d y}{d x} = \dfrac{ x}{ y cos(y^2)} \)
La pendenza \( m \) della retta tangente è data dal valore di \( \dfrac{d y}{d x} \) nel punto \( ( 0,\sqrt{\pi}) \).
\( m = \dfrac{(0)}{\sqrt{\pi} cos((\sqrt{{\pi}})^2)} = 0 \)
L'equazione, in forma di pendenza puntuale, della retta tangente alla curva nel punto \( ( 0,\sqrt{\pi}) \) è data da
\( y - \sqrt{\pi} = 0(x - 0) \)
È una linea orizzontale data da
\(y = \sqrt{\pi} \)
Soluzione alla domanda 8
\( f(x) \) è continuo sugli intervalli \( (-\infty , 1) \) , \( (1,2) \) e \( (2 , +\infty) \). Dobbiamo trovare \( a \) e \( b \) in modo che sia continua anche in \( x = 1 \) e \( x = 2 \) e quindi continua in \( (-\infty , +\ infty ) \).
\( f(1) = 1 \)
\( \lim_{x\to 1^-} f(x) = 1 \)
\( \lim_{x\to 1^+} f(x) = a(1)^3+b = a + b \)
I limiti da sinistra e da destra di \( 1 \) devono essere uguali
\( a + b = 1 \) (equazione 1)
\( f(2) = 2 + 2b\)
\( \lim_{x\to 2^-} f(x) = a(2)^3 + b = 8 a + b \)
\( \lim_{x\to 2^+} f(x) = 2 + 2 b \)
I limiti da sinistra e da destra di \( 2 \) devono essere uguali
\( 8 a + b = 2 + 2 b \) (equazione 2)
Risolvi le equazioni (1) e (2) simultaneamente per trovare
\( a = \dfrac{1}{3} \) e \( b = \dfrac{2}{3} \)
Soluzione alla domanda 9
Trova la derivata di \( y \).
\(y' = 1 + \cos(x) \)
La pendenza \( m \) della tangente in \( x = 0 \) è uguale al valore di \( y' \) in \( x = 0 \). Quindi
\( m = 1 + \cos(0) = 2 \)
La coordinata y del punto di tangenza \( P \) è data dal valore di \( y \) in \( x = 0 \). Quindi
\( P(0 , 0 + \sin(0)) = P(0,0) \)
L'equazione della retta tangente in forma di pendenza puntuale è data da
\(y - 0 = 2(x - 0) \)
e in forma di intercettazione del pendio
\(y = 2 x \)
Soluzione alla domanda 10 La definizione della derivata \( f' \) della funzione \( f \) è data dal limite
\( f'(x) = \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \)
Sostituisci \( f(x) \) con \( \sqrt{x+2} \) nella definizione precedente per ottenere
\( f'(x) = \lim_{h\to 0} \dfrac{\sqrt{x + h +2}- \sqrt{x+2} }{h} \)
Il limite di cui sopra è della forma indeterminata \( \dfrac{0}{0} \). Moltiplica il numeratore e il denominatore per il coniugato del numeratore
\( f'(x) = \lim_{h\to 0} \dfrac{ (\sqrt{x + h +2}- \sqrt{x+2} ) (\sqrt{x + h +2} + \ sqrt{x+2} ) }{h(\sqrt{x + h +2} + \sqrt{x+2} )} \)
Espandi il numeratore e semplifica
\( f'(x) = \lim_{h\to 0} \dfrac{ (x + h + 2)- (x + 2) ) }{h(\sqrt{x + h +2} + \sqrt{ x+2} )} = \lim_{h\to 0} \dfrac{ h }{h(\sqrt{x + h +2} + \sqrt{x+2} )}\)
Dividi numeratore e denominatore per \( h \) (o cancella \( h \))
\( f'(x) = \lim_{h\to 0} \dfrac{ 1 }{\sqrt{x + h +2} + \sqrt{x+2} }\)
Valutare il limite e quindi la derivata
\( f'(x) = \dfrac{ 1 }{ \sqrt{x + 0 + 2} + \sqrt{x + 2} } = \dfrac{ 1 }{2 \sqrt{x + 2} }\)
Soluzione alla domanda 11
Trova le derivate prima e seconda
\( f'(x) = e^x (x^2-5x+8) + e^x (2 x -5) +\dfrac{x^3}{3}-\dfrac{x^2}{ 2} = e^x (x^2-3x+3)+\dfrac{x^3}{3}-\dfrac{x^2}{2} \)
\( f''(x) = e^x(x^2-3x+3)+e^x(2x-3) + x^2-x = e^x(x^2-x)+x^ 2-x = x (x - 1) e^x \)
\( f'' \) ha due zeri: \( x = 0 \) e \( x = 1\) e \( e^x \) è sempre positivo. Quindi la tavola dei segni di \( f'' \) ha tre intervalli
1) \( (-\infty , 0 ) \) , valore di prova \( x = -1 \) , \( f''(-1) = 2/e \) , quindi \( f''(x) \) è positivo sull'intervallo \( (-\infty , 0 ) \).
2) \( (0 , 1 ) \) , valore test \( x = 1/2 \) , \( f''(1/2) = -\dfrac{\sqrt 2}{4} \) , quindi \( f''(x) \) è negativo sull'intervallo \( (0 , 1 ) \).
3) \( (1 , +\infty ) \) , valore test \( x = 2 \) , \( f''(2) = 2e^2 \) , \( f''(x) \) è positivo sull'intervallo \( (1 , +\infty ) \).
\( f'' \) è concava in alto sugli intervalli \( (-\infty , 0 ) \) e \( (1 , +\infty ) \) , e concava verso il basso sull'intervallo \( (0 , 1 ) \).
\( f'' \) cambia segno in \( x = 0 \) e \( x = 1 \) e quindi ha punti di flesso in \( x = 0 \) e \( x = 1 \).
Soluzione alla domanda 12
Il metodo di Newton si basa sul seguente algoritmo: conoscere un'approssimazione \( x_n \) alla soluzione di un equazione \( f(x) = 0 \), l'approssimazione successiva \( x_{n+1}\) dell'equazione è data da
\( x_{n+1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \).
La soluzione dell'equazione data \( e^x = x^3 \) è uguale alla soluzione dell'equazione \( f(x) = e^x - x^3 = 0 \)
\( f'(x) = e^x - 3x^2 \)
Conosciamo una prima approssimazione \( x_1 = 2 \); usando l'algoritmo di Newton approssimiamo \( x_2\) per
\( x_{2} = x_1 - \dfrac{f(x_1)}{f'(x_1)} = 2 - \dfrac{e^2 - 2^3}{e^2 - 3 \times 2^2} \approx 1,87 \) (arrotondato alla seconda cifra decimale)
Un'approssimazione \(x_3\) può essere ottenuta usando \( x_2 \) trovata sopra e così via.
Soluzione alla domanda 13
Trova la derivata prima e fattorizzala.
\( f'(x) = 4 x^3 - 3 x^2 = x^2(4x - 3)\)
\( f'(x) \) ha due zeri in \( x = 0 \) e \( x = 3/4 \) ed entrambi sono all'interno dell'intervallo \( [0,5] \). Gli zeri di \( f'(x) \) sono chiamati punti critici.
Valutiamo ora la funzione agli estremi dell'intervallo dato e agli zeri di \( f'(x) \).
\( f(0) = 0 \)
\( f(5) = 5^4 - 5^3 = 500 \)
\( f(3/4) = (3/4)^4 - (3/4)^3 = -\dfrac{27}{256} \)
Confrontando questi valori, \( f(x) \) ha un massimo assoluto pari a \(500 \) all'estremo \( x = 5 \) e un minimo assoluto pari a \( -\dfrac{27}{256} \) nel punto critico \( x = 3/4 \)
Sono incluse altre domande sul minimo e massimo assoluto di una funzione.
Soluzione alla domanda 14
Il volume \( V \) della scatola rettangolare di dimensioni \( L \),\( W \) e \( H\) è dato da
\( V = L(t) W(t) H(t) \)
dove \( L(t)\) , \( W(t) \) e \( H(t) \) sono funzioni del tempo \( t \).
Poiché le dimensioni della scatola cambiano nel tempo, anche il volume della scatola cambia nel tempo al tasso di cambiamento di \( V\) è dato dalla derivata prima \( \dfrac{dV}{dt} \).
\( \dfrac{dV}{dt} = W(t) H(t) \dfrac{d L}{dt } + L(t) H(t) \dfrac{d W}{dt } + L(t ) W(t) \dfrac{d H}{dt } \)
Sostituisci le quantità note con i loro valori numerici
\( \dfrac{dV}{dt} = 8 \times 5 \times 0.1 + 20 \times 5 \times (-0.2) + 20 \times 8 \times 0.3 = 32 \; cm^3 / sec \)
Soluzione alla domanda 15 Equazione di un cerchio con raggio \( 3 \) e centro in \( (0 , 0) \)dato di
\( x^2 + y^2 = 3^2 \)
Risolvi l'equazione precedente fo y
\(y^2 = 9 - x^2\)
\(y = \pm \sqrt{9 - x^2} \)
L'equazione per il semicricolo superiore è
\(y = \sqrt(9-x^2) \)
Un punto sul semicerchio con coordinata x \( x \) ha una coordinata y uguale a \(\sqrt{9 - x^2} \) (vedi grafico sotto)
Il rettangolo ha una lunghezza \( L = 2x \) e una larghezza (o altezza) \( W = \sqrt(9-x^2) \). L'area \( A \) del rettangolo è data da
\( A(x) = L \times W = 2 x \sqrt(9-x^2) \) , \( 0 \le x \le 3 \)
Trova la derivata prima di \( A \)
\( \dfrac{d A}{dx} = 2\sqrt{9-x^2} + (2x) (\dfrac{1}{2}) (-2x) (9-x^2)^{- 1/2} =\dfrac{2\left(-2x^2+9\right)}{\sqrt{9-x^2}} \)
Gli zeri di \( \dfrac{d A}{dx} \) sono dati dagli zeri del numeratore di \( \dfrac{d A}{dx} \)
\(-2x^2+9 = 0 \)
Restituisce due zeri: \( x = \sqrt{4.5} \) e \( x = - \sqrt{4.5} \)
Consideriamo lo zero in \( x = \sqrt{4.5} \) poiché è all'interno dell'intervallo \( [0 , 3 ] \)
Valutiamo ora l'area \( A(x) \) agli estremi \( x = 0 \) e \( x = 3 \) e nel punto critico \( x = \sqrt{4.5} \).
\( A(0) = 0 \)
\( A(3) = 0 \)
\( A(\sqrt{4.5}) = 9 \)
L'area A è massima è per \( x = \sqrt{4.5} \)
Le dimensioni sono:
\( L = 2 x = 2 \sqrt{4.5} \approx 4.24 \)
\( W = \sqrt(9-x^2) = \sqrt(9-\sqrt{4.5}^2) \approx 2.12 \)
Altri problemi di ottimizzazione inclusi.
\( \)\( \)\( \)\( \)\( \)
