We present the definitions of column and row spaces of a matrix using examples with detailed solutions.
Let A be an m × n matrix.
The column space of matrix A , denoted by Col A , is the set of all linear combinations of the columns of matrix A .
If
are the columns of matrix A , then
Note that the columns may not be independent and in what follows we look at examples on how to find the basis of Col A by selecting the independent columns only.
The rank of matrix A is the dimension of Col A which is given by the number of vectors in the basis of Col A .
Example 1
Find the basis of the column space and the rank of each of the matrices:
\( \) \( \) \( \)
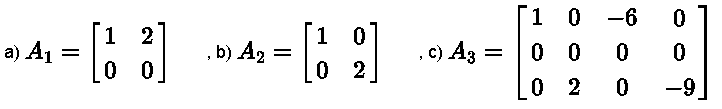
Solution to Example 1
a)
Let \( c_1 = \begin{bmatrix}
1 \\
0
\end{bmatrix}
\) and \( c_2 = \begin{bmatrix}
2 \\
0
\end{bmatrix}
\) be the columns of matrix \( A_1 \).
Note that \( c_2 = 2 c_1 \) and therefore \( c_1 \) and \( c_2 \) are NOT independent. As a result, we need one column only to span \( \text{Col}\; A_1 \).
hence the basis \( B \) of \( \text{Col} \; A_1 \) is given by: \( B = \{c_1\} \) or \( B = \left\{ \begin{bmatrix}
1 \\
0
\end{bmatrix} \right\} \)
\( \text{Col} \; A_1 = \text{span} \{c_1\} \)
The basis of \( \text{Col} \; A_1 \) has one vector and therefore \( \text{Rank} (A_1) = 1 \).
b)
Let \( c_1 = \begin{bmatrix}
1 \\
0
\end{bmatrix}
\) and \( c_2 = \begin{bmatrix}
0 \\
2
\end{bmatrix}
\) be the columns of matrix \( A_2 \). Note that \( c_1 \) and \( c_2 \) are independent. As a result, we need both columns \( c_1 \) and \( c_2 \) to span \( \text{Col}\; A_2 \).
The basis \( B \) of \( \text{Col} \; A_2 \) is given by: \( B = \{c_1,c_2\} \) or \( B = \left\{\begin{bmatrix}
1 \\
0
\end{bmatrix} , \begin{bmatrix}
0 \\
2
\end{bmatrix} \right\} \)
\( \text{Col} \; A_2 = \text{span} \{c_1,c_2\} \)
The basis of \( \text{Col} \; A_2 \) has two vectors and therefore \( \text{Rank} (A_2) = 2 \).
Example 2
Find the basis of the column space and the rank of matrix
\( A = \begin{bmatrix}
1 & -2 & 0 & 4\\
-1 & 3 & 1 & 0\\
0 & -1 & -1 & -4
\end{bmatrix}
\).
Solution to Example 2
As seen in example 1, the basis of \( Col \; A \) is given by the linearly independent columns of matrix \( A \). One way to find out which columns are linearly independent is to rewrite the given matrix in row echelon form (REF).
Rewrite matrix \( A \) in row echelon form
\( \color{red}{\begin{matrix}
\\
R_2+R_1\\
\\
\end{matrix}} \)
\( \begin{bmatrix}
1 & -2 & 0 & 4\\
0 & 1 & 1 & 4\\
0 & -1 & -1 & -4
\end{bmatrix}
\)
\( \color{red}{\begin{matrix}
\\
\\
R_3+R_2\\
\end{matrix}} \)
\( \begin{bmatrix}
\color{blue}1 & -2 & 0 & 4\\
0 & \color{blue}1 & 1 & 4\\
0 & 0 & 0 & 0
\end{bmatrix}
\)
The basis of \( \text{Col} \; A \) is given by the column in the original matrix corresponding to the columns with pivot (the leading 1 in a row) in the row echelon form obtained.
The first and second column in the reduced matrix has a pivot each and therefore the first and second column in the original matrix form the basis \( B \) of \( \text{Col}\ A \) which is given by
\( B = \left\{\begin{bmatrix}
1 \\
-1 \\
0
\end{bmatrix} , \begin{bmatrix}
-2 \\
3\\
-1
\end{bmatrix} \right\} \)
\( \text{Col}\ A = \text{span} \left\{ \begin{bmatrix}
1 \\
-1 \\
0
\end{bmatrix} , \begin{bmatrix}
-2 \\
3\\
-1
\end{bmatrix} \right\} \)
The basis of \( \text{Col} \; A \) has two vectors and therefore \( \text{Rank} (A) = 2 \).
Let \( A \) be an \( m \times n\) matrix.
The row space of matrix \( A \), denoted by \( \text{Row} A \), is the set of all linear combinations of the rows of matrix \( A \). If \( b_1, b_2, ..., b_m \) are the rows of matrix \( A \), then
\[ \text{Row} \; A = \text{span} \; \{b_1, b_2, ..., b_n\} \]
Note that the rows \( \{b_1, b_2, ..., b_m\} \)may not be independent and in what follows we look at examples on how to find the basis of \( \text{Row} \; A \) by selecting the independent rows only.
The rank of matrix \( A \) is the dimension of \( \text{Row} \; A \) which is given by the number of vectors in the basis of \( \text{Row} \; A \).
Example 3
Find the basis of the row space and the rank of each of the matrices:
a) \( A_1 = \begin{bmatrix}
4 & 8 \\
- 2 & - 4
\end{bmatrix}
\) , b) \( A_2 = \begin{bmatrix}
1 & 0 & 5\\
0 & 2 & 7
\end{bmatrix}
\)
,
c) \( A_3 = \begin{bmatrix}
1 & 0 & -6 & 0\\
0 & 0 & 0 & 0\\
0 & 2 & 0 & -9
\end{bmatrix}
\)
Solution to Example 3
a)
Let \(
b_1 = (4,8)
\) and \( b_2 = (-2,-4)
\) be the rows of matrix \( A_1 \). Note that \( b_2 = - \dfrac{1}{2} b_1 \) and therefore \( b_1 \) and \( b_2 \) are NOT independent. As a result, we need one row only to span \( \text{Row}\; A_1 \).
Hence the basis \( B \) of \( \text{Row} \; A_1 \) is given by: \( B = \{ b_1\} \) or \( B = \{ (4,8) \} \)
\( \text{Row} \; A_1 = \text{span} \{ (4,8) \} \)
The basis of \( \text{Row} \; A_1 \) has one vector and therefore \( \text{Rank} (A_1) = 1 \).
b)
Let \( b_1 = (1,0,5)
\) and \( b_2 = (0,2,7) \)
be the rows of matrix \( A_2 \). Note that \( b_1 \) and \( b_2 \) are independent. We therefore need both columns to span \( \text{Row} \; A_2 \).
The basis \( B \) of \( \text{Row} \; A_2 \) is given by: \( B = \{ b_1 , b_2 \} \) or \( B = \{ (1,0,5) , (0,2,7) \} \)
\( \text{Row} \; A_2 = \text{span} \{ (1,0,5) , (0,2,7) \} \)
The basis of \( \text{Row} \; A_2 \) has two vectors and therefore \( \text{Rank} (A_2) = 2 \).
c)
Let \( b_1 = (1,0,-6,0) \), \( b_2 = (0,0,0,0) \) and \( b_3 = (0,2,0,-9) \) be the rows of matrix \( A_3 \).
Note that \( b_1 \) and \( b_3 \) are independent; \( b_2 \) is a zero vector that does not contribute in any linear combination and therefore is not included in the basis.
The basis \( B \) of \( \text{Row} \; A_3 \) is given by: \( B = \{ b_1 , b_3 \} \) or \( B = \{ (1,0,-6,0) , (0,2,0,-9) \} \)
\( \text{Row} \; A_3 = \text{span} \{ (1,0,-6,0) , (0,2,0,-9) \} \)
The basis of \( \text{Row} \; A_3 \) has two vectors and therefore \( \text{Rank} (A_3) = 2 \).
Example 4
Find the basis of the row space and the rank of the matrix
\( A = \begin{bmatrix}
1 & -2 & 0 & 4\\
1 & 1 & -1 & - 8 \\
2 & -1 & -1 & -4 \\
- 3 & 3 & 1 & 0
\end{bmatrix}
\).
Solution to Example 4
We need to find independent rows among the rows of the given matrix. This can be done by rewriting the given matrix to row echelon form.
Rewrite matrix \( A \) in row echelon form
\( \color{red}{\begin{matrix}
\\
R_2 - R_1\\
R_3 - 2 R_1\\
R_4 + 3 R_1\\
\end{matrix}} \)
\( \begin{bmatrix}
1 & -2 & 0 & 4\\
0 & 3 & -1 & -12\\
0 & 3 & -1 & -12\\
0 & -3 & 1 & 12
\end{bmatrix}
\)
\( \color{red}{\begin{matrix}
\\
\frac{1}{3} R_2\\
\\
\\
\end{matrix}} \)
\( \begin{bmatrix}
1 & -2 & 0 & 4\\
0 & 1 & -1/3 & - 4\\
0 & 3 & -1 & -12\\
0 & -3 & 1 & 12
\end{bmatrix}
\)
\( \color{red}{\begin{matrix}
\\
\\
R_3 - 3 R_2\\
R_4 + 3 R_2\\
\end{matrix}} \)
\( \begin{bmatrix}
1 & -2 & 0 & 4\\
0 & 1 & -1/3 & - 4\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{bmatrix}
\) (I)
The basis of \( \text{Row} \; A \) is given by the nonzero rows in the row echelon form (matrix I) obtained. Hence
\( \text{Row}\ A = \text{span} \; \left\{ (1 , -2 , 0 , 4) , (0 , 1 , -1/3 , - 4) \right\} \)
The basis of \( \text{Row} \; A \) has two vector and therefore \( \text{Rank} (A) = 2 \).
If \( A \) is an \( m \times n \) matrix,
Step 1: Rewrite matrix \( A \) in a row echelon form as matrix \( E \)
Step 2: The basis of \( \text{Row} \; A \) is the set of all nonzero rows in matrix \( E \) and \( \text{Row} \; A \) is a subspace of \( \mathbb{R}^n \)
Step 3: The basis of \( \text{Col} \; A \) is the set of all columns in \( A \) corresponding to the columns with pivot in \( E \) and \( \text{Col} A \) is a subspace of \( \mathbb{R}^m \)
Step 4: Rank of A = dim\( \text{Row} \; A \) = dim \( \text{Col} \; A \)
Example 5
Find the basis of the row space, the basis of the column space and the rank of the matrix
\( A =
\begin{bmatrix}
-1 & 3 & 4 & -2\\
1 & 2 & -2 & 0\\
2 & -3 & 1 & 0\\
0 & 5 & 2 & -2
\end{bmatrix}
\).
Solution to Example 5
Step 1: Write matrix \( A \) in row echelon form \( E \)
Note that since writing matrices in row echelon is not the main topic discussed here, we have used a row reduce calculator to obtain the row echelon form \( E \) of the given matrix.
\( E =
\begin{bmatrix}
1 & -3 & -4 & 2\\
0 & 1 & 2/5 & -2/5\\
0 & 0 & 1 & -14/39\\
0 & 0 & 0 & 0
\end{bmatrix}
\)
Step 2: The basis \(B \) of \( \text{Row} A \) is the set of all nonzero rows in \( E \).
Hence \( B = \{ (1 , -3 , -4 , 2) , (0 , 1 , 2/5 , -2/5) , (0 , 0 , 1 , -14/39) \} \)
Step 3: The basis \( C \) of \( \text{Col} A \) is the set of all columns in \( A \) corresponding to the columns with pivots in \( E \).
The first three columns in \( E \) have a pivot hence the basis is the set of the first three columns in \( A \).
\( C = \left\{ \begin{bmatrix}
-1\\
1\\
2\\
0
\end{bmatrix} , \begin{bmatrix}
3\\
2\\
-3\\
5
\end{bmatrix} , \begin{bmatrix}
4\\
-2\\
1\\
2
\end{bmatrix} \right\} \)
Step 4: The dimensions of \( \text{Row} \; A \) and \( \text{Col} \; A \) are given by
dim \( \text{Row} \; A \) = number of rows in the basis \( B \) of \( \text{Row} \; A \) = 3
dim \( \text{Col} \; A \) = number of vetors in the basis \( C \) of \( \text{Col} \; A \) = 3
Rank of \( A \) = dim \( \text{Row} \; A \) = dim \( \text{Col} \; A \) = 3
Given matrix \( A \) and its row echelon form \( E \), determine the column space, the row space and the rank of each matrix.
