Los Los números complejos se escriben en forma polar (o trigonométrica). Las multiplicaciones y divisiones de números complejos en formas polares se explican mediante ejemplos y se refuerzan mediante preguntas con soluciones detalladas.
Números complejos en forma polar
Representemos el número complejo \( z = a + b \; i \) donde \(i = \sqrt{-1}\) en el plano complejo que es un sistema de ejes rectangulares, tal que la parte real \( a \) es la coordenada en el eje horizontal y la parte imaginaria \( b \) la coordenada en el eje vertical como se muestra a continuación.
dónde
\( r = \sqrt {a^2 + b^2} \) , \( r \) se llama módulo de \( z \)
\( tan (\theta) = \left (\dfrac{b}{a} \right) \) , tal que \( 0 \le \theta \lt 2\pi \) , \( \theta\) se llama argumento de \( z \).
El ángulo de referencia \( \theta_r \) del argumento \( \theta\) es un ángulo agudo formado por el eje horizontal y el lado terminal de \( \theta\) y se define de la siguiente manera:
\( \theta_r = tan^{-1} \left|\dfrac{b}{a} \right| \)
Si se conocen \( r \) y \( \theta \), entonces \( a \) y \(b \) están dados por
\( a = r \cos \theta \)
\( b = r \sin \theta \)
El número complejo \( z = a + b i \) se puede expresar en forma polar involucrando \(r\) y \( \theta \) de la siguiente manera
\[ z = r (\cos(\theta)+ i \sin(\theta)) \]
Ejemplo 1
a) Traza el número complejo \( z = 2\sqrt 3 - 2 i \) en el plano complejo y escríbelo en forma polar.
Solución al ejemplo 1
Vea el gráfico a continuación de la gráfica de \(z\) en un plano complejo.
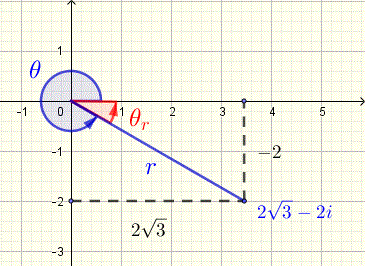
\( r = \sqrt {(2\sqrt 3)^2 + (2)^2} = 4\)
Necesitamos encontrar el ángulo de referencia \( \theta_r \) para encontrar el ángulo \( \theta \).
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1} \dfrac{\sqrt 3}{3} = \dfrac{\pi }{6}\)
La parte real de \(z\) es positiva y su parte imaginaria es negativa, por lo tanto, el lado terminal del argumento \( \theta \) está en el cuadrante IV (ver gráfico de \( z \) arriba).
Ahora calculamos \( \theta \) de la siguiente manera:
\( \theta = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{6} = \dfrac{11\pi}{6}\) (ver gráfico de \( z \))
\( z \) en forma polar viene dada por
\( z = 4 \left(\cos(\dfrac{11\pi}{6})+ i \sin(\dfrac{11\pi}{6}) \right) \)
Ejemplo 2
Escribe el número complejo \( z = \sqrt2(\cos(\dfrac{3\pi}{4})+ i \sin(\dfrac{3\pi}{4})) \) en forma estándar.
Solución al ejemplo 2
\( z = \sqrt2(\cos(\dfrac{3\pi}{4})+ i \sin(\dfrac{3\pi}{4})) \)
\( = \sqrt2(-\dfrac{\sqrt2}{2} + i \dfrac{\sqrt2}{2}) \)
\( = - 1 + i \)
Multiplicación y División de Números Complejos en Formas Polares
Sean \( z_1 = r_1 (\cos\theta_1 + i \sin\theta_1)\) y \( z_2 = r_2 (\cos\theta_2 + i \sin\theta_2) \) números complejos en forma polar. Usando la fórmula trigonométrica de suma y diferencia para el seno y el coseno, se puede demostrar que el producto y el cociente de estos dos los números complejos están dados por
\( z_1 z_2 = r_1 r_2 (\cos(\theta_1+\theta_2) + i\sin(\theta_1+\theta_2)) \)
\( \dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} (\cos(\theta_1-\theta_2) + i\sin(\theta_1-\theta_2)) \)
Ejemplo 3
Dado \( z_1 = 3 (\cos(5\pi/4) + i \sin(5\pi/4)) \) y \( z_2 = (\cos(\pi/4) + i \sin(\pi/4)) \)
Encuentre \( z_1 z_2\) y \( \dfrac{z_1}{z_2} \)
Solución al ejemplo 3
\( z_1 z_2 = 3 (\cos(5\pi/4) + i \sin(5\pi/4)) (\cos(\pi/4) + i \sin(\pi/4)) = 3 (\cos(5\pi/4+\pi/4) + i \sin(5\pi/4+\pi/4)) \)
\( = 3 (\cos(3\pi/2) + i \sin(3\pi/2)) \)
\( = - 3 i \)
\( \dfrac{z_1}{z_2} = \dfrac{3 (\cos(5\pi/4) + i \sin(5\pi/4))} {(\cos(\pi/4) + i \sin(\pi/4))} \)
\( = 3 (\cos(5\pi/4-\pi/4) + i \sin(5\pi/4-\pi/4)) \)
\( = 3 (\cos(\pi) + i \sin(\pi)) \)
\( = - 3 \)
Preguntas
1) Escribe los siguientes números complejos en formas polares.
\( z_1 = i \)
\( z_2 = 2 \)
\( z_3 = - 2 i \)
\( z_4 = - 3 \)
\( z_5 = \sqrt3 + i \)
\( z_6 = - 3 - 3\sqrt3 i \)
\( z_7 = - 5 + 5 i \)
.
2) Utilice los resultados de la parte 1 anterior para evaluar las siguientes expresiones en forma polar.
\( z_5 z_6 \)
\( \dfrac{z_6 z_7}{z_5} \)
.
Soluciones a las preguntas anteriores
1)
A continuación se muestran las gráficas de los números complejos \(z_1, z_2, z_3, z_4 \) en las preguntas a), b), c) y d). Estos gráficos ayudan a explicar cómo se encuentra el argumento para cada uno de estos números complejos que son reales (positivos o negativos) o imaginarios puros (parte imaginaria positiva o negativa).
\( z_1 = i \)
por eso \( r = \sqrt{0^2+1^2} = 1 \)
La gráfica de \( z_1 = i \) en el plano complejo da un punto en \( (0,1 ) \) con el lado terminal del argumento correspondiente (ángulo) en el eje vertical positivo y por lo tanto \( \theta = \pi/2\). (consulte el gráfico anterior para ver el argumento y el módulo)
\( z_1 \) en forma polar es: \( z_1 = \cos ( \pi/2) + i \sin(\pi/2) \)
\( z_2 = 2 \)
por eso \( r = \sqrt{2^2+0^2} = 2 \)
La gráfica de \( z_2 = 2 \) en el plano complejo da un punto \( (2 , 0) \) con el lado terminal del argumento correspondiente (ángulo) en el eje horizontal positivo y por lo tanto \( \theta = 0 \). (consulte el gráfico anterior para ver el argumento y el módulo)
\( z_2 \) en forma polar es: \( z_2 = 2 (\cos (0) + i \sin(0)) \)
\( z_3 = - 2 i \)
\( z_3 = 2( \cos(3\pi/2) + i \sin(3\pi/2)) \) (consulte el gráfico anterior para ver el argumento y el módulo)
\( z_4 = - 3 \)
por eso
\( z_4 = 3 ( \cos(\pi) + i \sin(\pi)) \) (consulte el gráfico anterior para ver el argumento y el módulo)
\( z_5 = \sqrt3 + i \)
por eso
\( r = \sqrt{(\sqrt3)^2+1^2} = 2 \)
Encuentre el ángulo de referencia \( \theta_r \) definido como el ángulo entre el eje horizontal y el lado terminal del argumento \( \theta \).
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1} \left| 1 / \sqrt3 \right| = \pi/6 \)
La parte real y las partes imaginarias son positivas y por lo tanto el lado terminal del argumento está en el cuadrante I. Por lo tanto
\( \theta = \theta_r = \pi / 6 \)
\( z_5 = 2 ( \cos(\pi/6) + i \sin(\pi/6)) \)
A continuación se muestra el diagrama de \(z_5\) con más explicaciones.
\( z_6 = - 3 - 3\sqrt3 i \)
por eso
\( r = \sqrt{(-3)^2+(-3\sqrt3)^2} = 6 \)
El ángulo de referencia \( \theta_r \) definido como el ángulo entre el eje horizontal y el lado terminal del argumento \( \theta \).
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1} \left |(- 3\sqrt3) / (- 3) \right| = \pi/3 \)
La parte real y la parte imaginaria son ambas negativas y por lo tanto el lado terminal del argumento está en el cuadrante III. Por eso
\( \theta = \pi + \theta_r = \pi + \pi/3 = 4 \pi/3\)
\( z_6 = 6 ( \cos(4\pi/3) + i \sin(4 \pi/3)) \)
\( z_7 = - 5 + 5 i \)
por eso
\( r = \sqrt{(-5)^2+(5)^2} = 5\sqrt2 \)
Encuentra el ángulo de referencia \( \theta_r\)
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1} | 5 / - 5| = \tan^{-1} (1) = \pi/4 \)
La parte real es negativa y la parte imaginaria es positiva y por tanto el lado terminal del argumento está en el cuadrante II. Por eso
\( \theta = \pi - \theta_r = \pi - \pi/4 = 3 \pi/4\)
\( z_7 = 5\sqrt2 ( \cos(3 \pi/4) + i \sin(3 \pi/4)) \)
.
2)
\(z_5\) y \(z_6\) ya se han expresado en forma polar, por lo tanto usamos la fórmula para el producto de dos números complejos en polar dada anteriormente.
\( z_5 z_6 = 2 ( \cos(\pi/6) + i \sin(\pi/6)) \;\; 6 ( \cos(4\pi/3) + i \sin(4 \pi/3)) \)
\( = (2\times6)( \cos(\pi/6 + 4\pi/3 ) + i \sin(\pi/6+4\pi/3)) = 12 ( \cos(3\pi/2) + i \sin(\cos(3\pi/2) ) \)
\( = - 12 i \)
Sustituye \(z_5\) , \(z_6\) y \(z_7\) por su forma polar encontrada arriba y usa ambas fórmulas para el producto en el numerador y la división.
\( \dfrac{z_6 z_7}{z_5} = \dfrac{6 ( \cos(4\pi/3) + i \sin(4 \pi/3)) \;\; 5\sqrt2 ( \cos(3 \pi/4) + i \sin(3 \pi/4))}{2 ( \cos(\pi/6) + i \sin(\pi/6))} \)
