Cómo encontrar el dominio de funciones racionales? Se presentan ejemplos junto con soluciones detalladas, explicaciones y también interpretación gráfica.
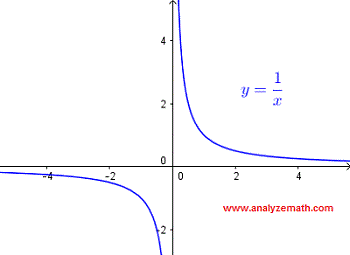
Primero necesitamos entender que \( \dfrac{1}{x} \) toma valores reales solo cuando el denominador no es igual a cero. Es decir, \( x \ne 0 \).
Esta restricción se puede verificar fácilmente examinando la gráfica de la función \( y = \dfrac{1}{x} \), que se muestra a continuación. La gráfica "existe" para todos los valores de \( x \) excepto en \( x = 0 \), donde la función no está definida.
El dominio de \( \dfrac{1}{x} \), en notación de intervalo, está dado por:
\[ (-\infty , 0) \cup (0 , \infty) \]

La función dada toma valores reales y por lo tanto está definida y es real para todos los valores de \( x \) excepto donde el denominador es cero.
Eso ocurre cuando:
\[ x - 2 \ne 0 \quad \Rightarrow \quad x \ne 2 \]En notación de intervalo, el dominio de la función es:
\[ (-\infty , 2) \cup (2 , \infty) \]La gráfica de la función \( f(x) = \dfrac{1}{x - 2} \) se muestra a continuación. La función no está definida en \( x = 2 \), lo cual es claramente visible como una asíntota vertical en la gráfica.

La función dada toma valores reales y por lo tanto es real si:
\[ (x - 1)(x + 2) \ne 0 \]Esta desigualdad es verdadera cuando \( x \ne 1 \) y \( x \ne -2 \).
En notación de intervalo, el dominio de la función es:
\[ (-\infty , -2) \cup (-2 , 1) \cup (1 , \infty) \]A continuación se muestra la gráfica de la función \( f(x) = \dfrac{x + 3}{(x - 1)(x + 2)} \), y podemos observar que la función no está definida en \( x = -2 \) y \( x = 1 \). En estas ubicaciones tenemos asíntotas verticales.

La función dada toma valores reales y por lo tanto está definida y es real si el denominador no es igual a cero:
\[ x^2 - 4 \ne 0 \]Factoriza \( x^2 - 4 \) y reescribe la desigualdad como:
\[ (x - 2)(x + 2) \ne 0 \]La expresión \( (x - 2)(x + 2) \) no es igual a cero si:
\[ x \ne -2 \quad \text{y} \quad x \ne 2 \]En notación de intervalo, el dominio de la función está dado por:
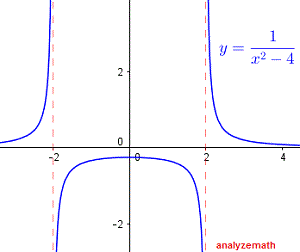
\[ (-\infty , -2) \cup (-2 , 2) \cup (2 , \infty) \]A continuación se muestra la gráfica de la función \( f(x) = \frac{1}{x^2 - 4} \), y podemos ver que la función no está definida en \( x = -2 \) y \( x = 2 \):
La función dada toma valores reales y por lo tanto es real si:
\[ x^2 + x - 2 \ne 0 \]Factoriza \( x^2 + x - 2 \) y reescribe la desigualdad como:
\[ (x - 1)(x + 2) \ne 0 \]La expresión \( (x - 1)(x + 2) \) no es igual a cero si \( x \ne 1 \) y \( x \ne -2 \).
En forma de intervalo, el dominio está dado por:
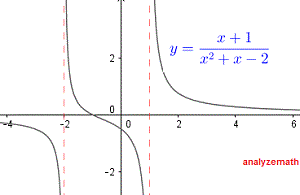
\[ (-\infty, -2) \cup (-2, 1) \cup (1, \infty) \]A continuación se muestra la gráfica de la función \( f \), y podemos ver que la función dada no está definida en \( x = -2 \) y \( x = 1 \).
La función dada toma valores reales y por lo tanto es real si:
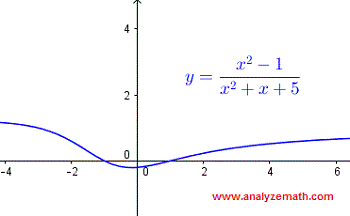
\[ x^2 + x + 5 \ne 0 \]La expresión \( x^2 + x + 5 \) no se puede factorizar sobre los reales. Por lo tanto, resolvemos la ecuación cuadrática usando el discriminante \( \Delta \):
\[ x^2 + x + 5 = 0 \] \[ \Delta = b^2 - 4ac = (1)^2 - 4(1)(5) = -19 \]El discriminante es negativo, por lo que no hay valores reales de \( x \) que hagan que la expresión \( x^2 + x + 5 \) sea igual a cero. Así, el dominio de la función es el conjunto de todos los números reales.
En notación de intervalo, el dominio es:
\[ (-\infty, \infty) \]A continuación se muestra la gráfica de la función \( f(x) = \dfrac{x^2 - 1}{x^2 + x + 5} \), y podemos ver que está definida para todos los valores reales de \( x \).