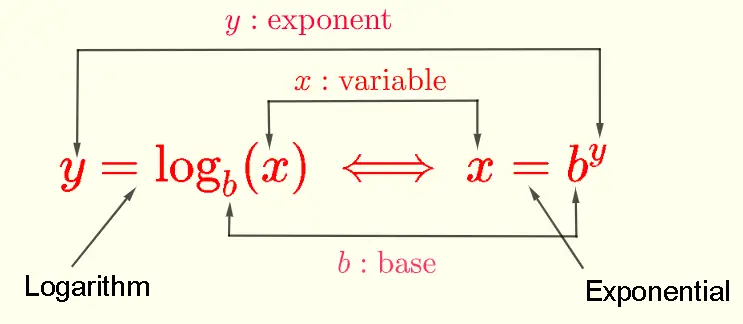
donde el símbolo \( \iff \) significa "es equivalente a", \( y \) es el exponente, \( b \) es la base tal que \( b \gt 0 , b \ne 1 \) y \( x \gt 0 \).
Preguntas sobre Logaritmos y Exponenciales con respuestas y soluciones detalladas, para grado 11, se presentan aquí.
Contenido de la Página
1) Una de las propiedades más importantes de las funciones logarítmicas y exponenciales es que son inversas entre sí, por lo tanto podemos convertir expresiones exponenciales y logarítmicas usando lo siguiente:
donde el símbolo \( \iff \) significa "es equivalente a", \( y \) es el exponente, \( b \) es la base tal que \( b \gt 0 , b \ne 1 \) y \( x \gt 0 \).
Ejemplo numérico \[ 2 = \log_3 (9) \iff 9 = 3^2 \]
2) Propiedades uno a uno de las funciones logarítmicas y exponenciales:
a) Si \( \quad b^x = b^y \quad \), entonces \( \quad x = y \).
b) Si \( \quad \log_b (x) = \log_b (y) \quad \), entonces \( \quad x = y \) (NOTA: los logaritmos en ambos lados tienen la misma base).
Usa las expresiones equivalentes: \( y = \log_b(x) \iff x = b^y \) para escribir:
a) \( \log_x (a) = c \) como una exponencial \( a = x^c \)
b) \( \log_b (2x + 1) = 3 \) como una exponencial \( 2x + 1 = b^3 \)
Usa las expresiones equivalentes: \( x = b^y \iff y = \log_b (x) \) para escribir:
a) \( 3^x = m \) como un logaritmo \( x = \log_3 (m) \)
b) \( x^2 = a \) como un logaritmo \( 2 = \log_x (a) \)
Usa las expresiones equivalentes: \( y = \log_b(x) \iff x = b^y \) para evaluar lo siguiente sin calculadora:
a)
Sea \[ y = \log_2 16 \]. Convierte a forma exponencial: \[ 2^y = 16 \]. Usa el hecho que \( 16 = 2^4\) para escribir \[ 2^y = 2^4 \]. Por lo tanto, usando la propiedad uno a uno de la exponencial dada arriba, "Si \( 2^y = 2^4 \), entonces y = 4", escribimos: \[ y = \log_2 16 = 4 \].
b)
Sea \[ y = \log_3 27 \]. Convierte a forma exponencial: \[ 3^y = 27 \]. Usa el hecho que \( 27 = 3^3 \) para escribir \[ 3^y = 3^3 \]. Por lo tanto, usando la propiedad uno a uno 2 b) da \[ y = 3 \]. Así: \[ y = \log_3 27 = 3 \].
c)
Sea \[ y = \log_2 (1/32) \]. Convierte a forma exponencial: \[ 2^y = \dfrac{1}{32} \]. Usa el hecho que \( \dfrac{1}{32} = \dfrac{1}{2^5} = 2^{-5} \) para escribir \[ 2^y = 2^{-5} \]. Y la propiedad uno a uno de la función exponencial da: \[ y = -5 \]. Por lo tanto \[ y = \log_2 (1/32) = -5 \].
d)
Sea \[ y = \log_{25} 5 \]. Convierte a forma exponencial: \[ 25^y = 5 \]. Usa el hecho que \( 5 = \sqrt{25} = 25^{1/2} \) para escribir \[ 25^y = 25^{1/2} \]. Por lo tanto \[ y = \log_{25} 5 = 1/2 \].
e)
Sea \( y = \log \sqrt{10} \) (nota: logaritmo base 10). Convierte a forma exponencial: \[ 10^y = \sqrt{10} = 10^{1/2} \]. Por lo tanto \[ y = \log \sqrt{10} = 1/2 \].
f)
Sea \( y = \log_b 1 \). Convierte a forma exponencial: \[ b^y = 1 = b^0 \quad \text{por lo tanto} \quad y = \log_b 1 = 0 \].
g)
Sea \( y = \log_{0.1} 10 \). Convierte a forma exponencial: \[ 0.1^y = 10 \]. Usa \( 10 = 1 / 0.1 = 0.1^{-1} \), por lo tanto \[ 0.1^y = 0.1^{-1} \quad \text{ lo que da } \quad y = \log_{0.1} 10 = - 1 \].
Usa las expresiones equivalentes: \( y = \log_b(x) \iff x = b^y \) para resolver para \( x \) las siguientes ecuaciones logarítmicas:
a)
\( \log_2 x = 3 \) ; convierte a forma exponencial: \[ x = 2^3 = 8 \]
b)
\( \log_x 8 = 3 \) ; convierte a forma exponencial: \[ 8 = x^3 \] escribe 8 como \[ 8 = 2^3 = x^3\] por lo tanto \[ x = 2 \]
c)
\( \log_3 x = 1 \) ; convierte a forma exponencial: \[ x = 3^1 = 3 \]
d)
\( \log_{5.6} x = 0 \) ; convierte a forma exponencial: \[ x = 5.6^0 = 1 \]
e)
\( \log_2 (3x + 1) = 4 \) ; convierte a forma exponencial: \[ 3x + 1 = 2^4 = 16 \] resuelve para x: \[ 3x + 1 = 16 , 3x = 15 , x = 5 \]
f)
\( \log_3 \dfrac{1}{x+1} = 2 \) ; convierte a forma exponencial: \[ \dfrac{1}{x+1} = 3^2 = 9 \] resuelve para x: \[ 1 = 9 (x + 1) , x = - 8 / 9 \]
g)
\( \log_4 \dfrac{x+1}{2x-1} = 0 \) ; convierte a forma exponencial: \[ \dfrac{x+1}{2x-1} = 4^0 = 1 \] resuelve para x: \[ x + 1 = 2x - 1 , x = 2 \]
h)
\( \log ( 1/x + 1 ) = 2 \) ; convierte a forma exponencial: \[ 1/x + 1 = 10^2 = 100 \] resuelve para x: \[ 1/x + 1 = 100 , 1/x = 99 , x = 1/99 \]
i)
\( \log_x 0.0001 = 4 \) ; convierte a forma exponencial: \[ x^4 = 0.0001 = 1/10000 = 1/10^4 = (1/10)^4 \] lo que da \[ x^4 = (1/10)^4 \] por lo tanto \[ x = 1/10 \].
Usa la propiedad uno a uno: si \( b^x = b^y \) entonces \( x = y \) para resolver las funciones exponenciales:
Nota que en la ecuación anterior, las bases de las dos exponenciales son iguales a \( b \).
a)
\( 3^x = 9 = 3^2 \) por lo tanto \[ x = 2 \]
b)
\( 4^{2x + 1} = 16 = 4^2 \), lo que da \[ 4^{2x + 1} = 4^2 \] por lo tanto \[ 2x + 1 = 2 , x = 1 / 2 \]
c)
\( \left(\dfrac{1}{2} \right)^x = 2 \). Escribe \( 2 \) como \[ 2 = \left(\dfrac{1}{2} \right)^{-1} \]. Lo que da \[ \left(\dfrac{1}{2} \right)^x = \left(\dfrac{1}{2} \right)^{-1} \]. Por lo tanto \[ x = - 1 \]
d)
\( 10^x = 5 \), convierte la exponencial a logaritmo base 10: \[ \quad x = \log_{10} 5 \]
e)
\( \left(\dfrac{1}{3} \right)^{x/2 - 2} = 9 = 3^2 \). Escribe \( 3^2 \) como \[ \left(\dfrac{1}{3} \right)^{-2} \]. Lo que da \[ \left(\dfrac{1}{3} \right)^{x/2 - 2} = \left(\dfrac{1}{3} \right)^{-2} \]. Por lo tanto \[ x/2 - 2 = - 2 \]. Resuelve para obtener \[ x = 0 \]
f)
\( 0.01^x = 100 \). Escribe: \[ 100 = \dfrac{1}{0.01} = 0.01^{-1} \quad \text{lo que da} \quad 0.01^x = 0.01^{-1} \]. Por lo tanto \[ x = -1 \]
g)
Dada la ecuación: \[ 2^{2x} - 6 \cdot 2^x = - 8 \]. Nota que \[ 2^{2x} = (2^x)^2 \]. Sea \( u = 2^x \) y escribe \[ u^2 = (2^x)^2 = 2^{2x} \]. Sustituimos \( 2^x \) por \( u \) y \( 2^{2x} \) por \( u^2 \) en la ecuación dada y reescribimos la ecuación en términos de \( u \) solo y en forma estándar como sigue: \[ u^2 - 6 u + 8 = 0 \]. Resuelve la ecuación cuadrática factorizando: \[ (u - 2)(u - 4) = 0 \]. Soluciones en u: \[ u = 2 \quad \text{y} \quad u = 4 \]. Ahora resolvemos para \( x \) usando la sustitución hecha arriba: \[ u = 2 = 2^x \quad \text{da la solución:} \quad x = 1 \] \[ u = 4 = 2^x = 2^2 \quad \text{da la solución:} \quad x = 2 \]