Esta página explica cómo bosquejar y graficar las funciones tangente y cotangente de la forma: \[ y = a \tan \big[ k ( x - d) \big] \quad \text{y} \quad y = a \cot \big[ k ( x - d) \big] \] con ejemplos detallados para ayudar a los estudiantes a comprender su comportamiento y transformaciones gráficas.
El rango de ambas funciones es \((- \infty , +\infty)\). El período de cada una es \(\pi\).
El desplazamiento horizontal está dado por \(d\); si \((-d)\) es positivo, la gráfica se desplaza a la izquierda, y si es negativo, a la derecha.
Las asíntotas verticales ocurren en:
\[ x = \dfrac{\pi}{2} + k\pi, \quad k = 0, \pm 1, \pm 2, \ldots \]
para \(y = \tan(x)\), y en:
\[ x = k\pi, \quad k = 0, \pm 1, \pm 2, \ldots \]
para \(y = \cot(x)\).
Para comprender las propiedades clave, recuerda las identidades:
\[ y = \tan(x) = \dfrac{\sin(x)}{\cos(x)} \quad \text{y} \quad y = \cot(x) = \dfrac{\cos(x)}{\sin(x)}. \]
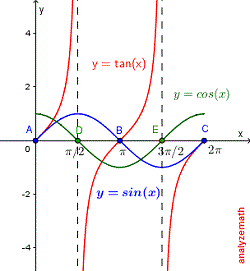
Todos los ceros de \(\sin(x)\) corresponden a ceros de \(\tan(x)\). Todos los ceros de \(\cos(x)\) (en el denominador) corresponden a asíntotas verticales de \(\tan(x)\), como se muestra.

Todos los ceros de \(\cos(x)\) corresponden a ceros de \(\cot(x)\). Todos los ceros de \(\sin(x)\) (en el denominador) corresponden a asíntotas verticales de \(\cot(x)\), como se muestra.

Bosqueja la gráfica de: \[ y = \tan\left( 2x + \dfrac{\pi}{2} \right) \] en un período.
Parámetros de la gráfica
Rango: \((- \infty , +\infty)\).
Período: \(\dfrac{\pi}{|k|} = \dfrac{\pi}{2}\).
Asíntotas verticales donde:
\[ 2x + \dfrac{\pi}{2} = \dfrac{\pi}{2} + k\pi \]
que se simplifica a:
\[ x = \dfrac{k\pi}{2}, \quad k = 0, \pm 1, \pm 2, \ldots \]
El desplazamiento horizontal permite reescribir la función como: \[ y = \tan \big[ 2 ( x + \dfrac{\pi}{4} ) \big]. \] Esto significa un desplazamiento de \(\dfrac{\pi}{4}\) unidades a la izquierda.
Dos pasos para graficar \( y = \tan\left( 2x + \dfrac{\pi}{2} \right) \):
1) Bosqueja \(\tan(2x)\) en un período de \(0\) a \(\dfrac{\pi}{2}\) (gráfica azul).
2) Luego bosqueja:
\[ y = \tan \big[ 2 ( x + \dfrac{\pi}{4} ) \big] \]
trasladando la gráfica anterior \(\dfrac{\pi}{4}\) a la izquierda (gráfica roja), haciendo que el período comience en \(- \dfrac{\pi}{4}\) y termine en \(\dfrac{\pi}{4}\) (un período completo de longitud \(\dfrac{\pi}{2}\)).

Bosqueja la gráfica de: \[ y = \cot \left( 4x - \dfrac{\pi}{4} \right) \] en un período.
Parámetros de la gráfica
Rango: \((- \infty , +\infty)\).
Período: \(\dfrac{\pi}{|k|} = \dfrac{\pi}{4}\).
Asíntotas verticales donde:
\[ 4x - \dfrac{\pi}{4} = k \pi \]
que da:
\[ x = \dfrac{k \pi + \dfrac{\pi}{4}}{4}, \quad k = 0, \pm 1, \pm 2, \ldots \]
Reescribimos el desplazamiento como: \[ y = \cot \left[ 4 \left( x - \dfrac{\pi}{16} \right) \right]. \] Esto representa un desplazamiento de \(\dfrac{\pi}{16}\) unidades a la derecha.
Dos pasos para graficar \( y = \cot \left( 4x - \dfrac{\pi}{4} \right) \):
1) Bosqueja \(\cot(4x)\) en un período de \(0\) a \(\dfrac{\pi}{4}\) (gráfica azul).
2) Luego bosqueja:
\[ y = \cot \left[ 4 \left( x - \dfrac{\pi}{16} \right) \right] \]
trasladando la gráfica \(\dfrac{\pi}{16}\) a la derecha (gráfica roja), haciendo que el período comience en \(\dfrac{\pi}{16}\) y termine en \(\dfrac{5\pi}{16}\) (un período completo).
