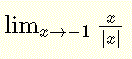
Solución
Los pasos para encontrar el límite son:

Cómo encontrar los límites de funciones de valor absoluto; se presentan varios ejemplos y soluciones detalladas junto con interpretaciones gráficas. Se presentan un conjunto de ejercicios con respuestas al final de la página.
Encuentra el límite: 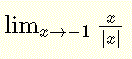
Solución
Los pasos para encontrar el límite son:

Evalúa el límite: 
Solución
Los pasos para encontrar el límite son

Encuentra el límite:
\(
\lim_{x \to 0} \frac{x}{|x|}
\)
Solución
\(
\lim_{x \to 0} \frac{x}{|x|} = \frac{0}{|0|} \; \; \text{forma indeterminada}
\)
Recuerda que
\( | x | = x \) para \( x \le 0 \) y \( | x | = - x \) para \( x \lt 0 \)
Calculemos el límite desde la izquierda de \( x = 0 \) donde \( x \lt 0 \) y por lo tanto \( | x | = - x \)
\(
\lim_{x \to 0^-} \frac{x}{|x|} = \lim_{x \to 0^-} \frac{x}{- x} = \lim_{x \to 0^-} - 1 = -1
\)
Calculemos el límite desde la derecha de \( x = 0 \) donde \( x \gt 0 \) y por lo tanto \( | x | = x \)
\(
\lim_{x \to 0^+} \frac{x}{|x|} = \lim_{x \to 0^+} \frac{x}{x} = \lim_{x \to 0^+} 1 =1
\)
Los límites desde la izquierda y desde la derecha de x = 0 no son iguales, por lo tanto
\(
\lim_{x \to 0} \frac{x}{|x|} \; \; \text{no existe}
\)
El gráfico de f(x) = x / |x| se muestra a continuación y claramente vemos que los límites desde la izquierda y desde la derecha de 0 no son iguales.

Evalúa el límite:
\(
\lim_{x \to \infty} \frac{x}{|x|}
\)
Solución
a medida que x aumenta indefinidamente, x > 0 y por lo tanto |x| = x
Por lo tanto
\(
\lim_{x \to \infty} \frac{x}{|x|} = \lim_{x \to \infty} \frac{x}{x} = \lim_{x \to \infty} 1 = 1
\)
Encuentra el límite:
\(
\lim_{x \to -\infty} \frac{x}{|x|}
\)
Solución
a medida que x disminuye indefinidamente, x < 0 y por lo tanto |x| = - x
Por lo tanto
\(
\lim_{x \to -\infty} \frac{x}{|x|} = \lim_{x \to -\infty} \frac{x}{ - x} = \lim_{x \to \infty} - 1 = - 1
\)
¿Existe el límite
\(
\lim_{x \to - 2} \frac{|x + 2|}{x + 2}
\)
?
Solución
\(
\lim_{x \to - 2} \frac{|x + 2|}{x + 2} = \lim_{x \to - 2} \frac{|- 2 + 2|}{- 2 + 2} = \dfrac{0}{0} \;\; \text{indeterminado}
\)
Calculemos el límite desde la izquierda de -2 donde x ≤ - 2 y desde la derecha de -2 donde x ≥ - 2 por separado.
Recuerda que
Si x + 2 ≥ 0 o x ≥ - 2 entonces | x + 2 | = x + 2
y
Si x + 2 ≤ 0 o x ≤ - 2 entonces | x + 2 | = - \( ( x + 2 ) \)
Calculemos el límite desde la izquierda de x = - 2.
\(
\lim_{x \to - 2^-} \frac{|x + 2|}{x + 2} = \lim_{x \to -2^-} \frac{-(x + 2)}{x + 2} = \lim_{x \to -2^-} - (x + 3) = - 4
\)
Calculemos el límite desde la derecha de x = - 2
\(
\lim_{x \to - 2^+} \frac{|x + 2|}{x + 2} = \lim_{x \to - 2^+} \frac{x + 2}{x + 2} = \lim_{x \to -2^+} 1 = 1
\)
Los límites desde la izquierda y desde la derecha de x = - 2 no son iguales, por lo tanto
\(
\lim_{x \to - 2} \frac{|x + 2|}{x + 2} \; \; \text{no existe}
\)
Encuentra el límite:
\(
\lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|}
\)
Solución
\(
\lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} = \frac{(1)^2+2(1)-3}{|(1) - 1|} = \dfrac{0}{0} \; \; \text{indeterminado}
\)
En x = 1 tanto el numerador como el denominador son iguales a cero, por lo tanto tienen un factor común x - 1. Factoricemos el numerador.
\(
\lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} = \lim_{x \to 1} \frac{(x-1)(x+3)}{|x - 1|}
\)
Recuerda que
| x - 1 | = x - 1 para x - 1 ≥ 0 o x ≥ 1
y
| x - 1 | = - \( ( x - 1 ) \) para x - 1 < 0 o x < 1
Calculemos el límite desde la izquierda de x = 1
\(
\lim_{x \to 1^-} \frac{x^2+2x-3}{|x - 1|} = \lim_{x \to 1^-} \frac{(x-1)(x+3)}{-(x-1)} = \lim_{x \to 1^-} - (x + 3) = - 4
\)
Calculemos el límite desde la derecha de x = 1
\(
\lim_{x \to 1^+} \frac{x^2+2x-3}{|x - 1|} = \lim_{x \to 1^+} \frac{(x-1)(x+3)}{x-1} = \lim_{x \to 1^-} (x + 3) = 4
\)
Los límites desde la izquierda y desde la derecha no son iguales, por lo tanto
\(
\lim_{x \to 1} \frac{x^2+2x-3}{|x - 1|} \; \; \text{no existe}
\)
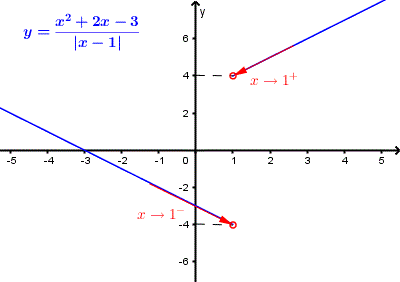
El gráfico de \( f(x) = \frac{x^2 + 2 x - 3}{|x - 1|} \) se muestra a continuación y claramente vemos que los límites desde la izquierda y desde la derecha de 1 no son iguales.
Evalúa el límite:
\(
\lim_{x \to \infty} \frac
{x^2+5x+7}{|x + 2|}
\)
Solución
A medida que x aumenta indefinidamente, x + 2 también aumenta indefinidamente y por lo tanto x + 2 > 0, por lo tanto
\(
\lim_{x \to \infty} \frac{x^2+5x+7}{|x + 2|} = \lim_{x \to \infty} \frac{x^2+5x+7}{x + 2} = + \infty
\)
Encuentra el límite:
\(
\lim_{x \to - \infty} \frac{x^2+5x+7}{|x + 2|}
\)
Solución
A medida que x disminuye indefinidamente, x + 2 también disminuye indefinidamente y por lo tanto x + 2 < 0, por lo tanto
\(
\lim_{x \to -\infty} \frac{x^2+5x+7}{|x + 2|} = \lim_{x \to -\infty} \frac{x^2+5x+7}{-(x + 2)} = + \infty
\)
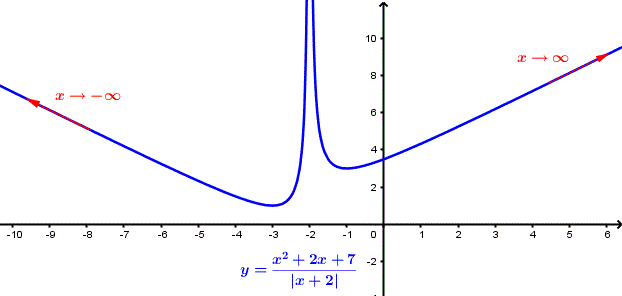
El gráfico de \( f(x) = \frac{x^2 + 5 x + 7}{|x + 2|} \) se muestra a continuación y claramente vemos que \( y = f(x) \) aumenta indefinidamente a medida que x aumenta indefinidamente y también a medida que x disminuye indefinidamente.
Encuentra los límites
1) \(
\lim_{x \to 0} \frac{x^2}{|x|}
\)
2) \(
\lim_{x \to - 6^-} \frac{-(x + 6)}{|x + 6|}
\)
3) \(
\lim_{x \to - 6^+} \frac{-(x + 6)}{|x + 6|}
\)
4) \(
\lim_{x \to 3} \frac{x^2-x-6}{|x - 3|}
\)
1) 0
2) 1
3) - 1
4) no existe