Löse die Gleichungssysteme.
a) \[ \begin{cases} -2(x-2) + (-y-3) = 3 \\ 2(x+3) - 3(y-2) = 10 \end{cases} \] Expandiere die linken Seiten und schreibe das Gleichungssystem in Standardform mit konstanten Termen auf der rechten Seite um. \[ \begin{cases} \color{red}{-2x - y} = \color{red}{2} \quad \text{(I)} \\ \color{blue}{2x - 3y} = \color{blue}{-2} \quad \text{(II)} \end{cases} \]
Addiere die linken Terme und die rechten Terme der Gleichungen (I) und (II), um die Terme mit x zu eliminieren. \[ (\color{red}{-2x - y}) + (\color{blue}{2x - 3y}) = (\color{red}{2}) + (\color{blue}{-2}) \] Vereinfache, um eine Gleichung mit einer Unbekannten zu erhalten. \[ -4 y = 0 \] Löse nach \( y \) auf, um zu erhalten
\[ y = 0 \] Setze \( y = 0 \) in Gleichung (I) (oder (II)) ein, um zu erhalten
\( \quad -2x-(0) = 2 \)
Löse die obige Gleichung nach \( x \) auf, um zu erhalten
\( \quad x = - 1 \)
Die Lösung des gegebenen Gleichungssystems ist das geordnete Paar
\[ (-1,0) \]
b)
\[ \quad \begin{cases} \displaystyle \frac{x-1}{3} + y & = & 5 \\ 2(x+3) - \frac{y}{5} & = & 7\end{cases} \]
Um die Nenner in den beiden Gleichungen des gegebenen Systems zu eliminieren, multipliziere alle Terme der ersten Gleichung mit \( 3 \) und alle Terme der zweiten Gleichung mit \( 5 \).
\( \quad \begin{cases} \displaystyle \color{red}{3}\frac{x-1}{3} + \color{red}{3} y & = & \color{red}{3} \cdot 5 \\ \displaystyle \color{red}{5} ( 2(x+3) ) - \color{red}{5} \frac{y}{5} & = & \color{red}{5} \cdot 7\end{cases} \)
Expandiere, vereinfache und schreibe das Gleichungssystem in Standardform um.
\( \quad \begin{cases} \displaystyle x + 3 y & = & 16 \\ 10 x - y & = & 5\end{cases} \)
Um die Terme in \( y \) zu eliminieren, multipliziere alle Terme der zweiten Gleichung mit 3.
\( \quad \begin{cases} \displaystyle x + 3 y & = & 16 \\ \color{red}3(10 x - y) & = & \color{red}3 \cdot 5\end{cases} \)
Expandiere
\( \quad \begin{cases} \displaystyle x + 3 y & = & 16 \qquad (I) \\ 30 x - 3y & = & 15 \qquad (II) \end{cases} \)
Addiere die linken Seiten der Gleichungen und die rechten Seiten, um die Terme in y zu eliminieren.
\( \quad 31 x = 31 \)
Löse nach \( x \) auf
\( \quad x = 1 \)
Setze \( x = 1 \) in Gleichung (I) (oder Gleichung (II)) ein
\( \quad (1) + 3 y = 16 \)
Löse nach \( y \) auf
\( \quad y = 5 \)
Die Lösung des gegebenen Gleichungssystems ist das geordnete Paar
\[ (1,5) \]
c)
\[ \displaystyle \quad \begin{cases} (x-1)^2 + y & = & -1 \qquad (I) \\ - 4 x + 2y & = & -6 \qquad (II) \end{cases} \]
Löse Gleichung (II) nach y auf, um zu erhalten
\( \quad y = 2x - 3 \qquad (III) \)
Setze \( y = 2x - 3 \) in Gleichung (II) ein und schreibe um als
\( \quad (x-1)^2 + \color{red}{(2x - 3)} = -1 \)
Expandiere und schreibe in Standardform um \( \quad x^2 - 1 = 0 \)
Löse die obige Gleichung nach \( x \) auf, um die Lösungen zu erhalten \( \quad x = 1 \) und \( x = - 1\)
Nachdem wir die Lösungen \( x \) gefunden haben, setzen wir jeden Wert der Lösungen \( 1 \) und \( -1 \) in Gleichung (III) ein, um die entsprechenden Werte der Lösungen \( y \) zu erhalten.
Setze \( x = 1 \) in Gleichung (III) ein, um zu erhalten
\( \quad y = 2(1) - 3 = -1 \)
Setze \( x = - 1 \) in Gleichung (III) ein, um zu erhalten
\( \quad y = 2(-1) - 3 = - 5 \)
Die beiden geordneten Paare, die Lösungen des gegebenen Gleichungssystems sind, sind
\[ (1,-1) \quad \text{und} \quad (-1,-5) \]
Expandiere und vereinfache die Ausdrücke.
a)
\( \quad -(x+2)(x-1) + (x-2)^2 \)
Expandiere das Produkt \( (x+2)(x-1) \) und das Quadrat \( (x-2)^2 \)
\( \quad (x+2)(x-1) = x^2+x-2 \)
\( \quad (x-2)^2 = x^2 - 4x + 4 \)
Setze das Obige in den gegebenen Ausdruck ein
\( \quad -(x+2)(x-1) + (x-2)^2 = - (x^2+x-2 ) + (x^2 - 4x + 4 ) \)
Löse die Klammern auf, indem du die Vorzeichen für Ausdrücke mit einem Minuszeichen davor änderst.
\( \quad -(x+2)(x-1) + (x-2)^2 = - x^2 - x + 2 + x^2 - 4x + 4 \)
Fasse gleiche Terme zusammen und vereinfache.
\[ \quad -(x+2)(x-1) + (x-2)^2 = -5x+6 \]
b)
\( \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) \)
Expandiere die Produkte \( (x-2)(x^2 + 3x -3) \) und \( (x-1)(x+1) \).
\( \quad (x-2)(x^2 + 3x -3) = x^3+x^2-9x+6 \)
\( \quad (x-1)(x+1) = x^2 - 1\)
Setze das Obige in den gegebenen Ausdruck ein
\( \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) = (x^3+x^2-9x+6) - (x^2 - 1) \)
Löse die Klammern auf, indem du die Vorzeichen für Ausdrücke mit einem Minuszeichen davor änderst.
\( \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) = x^3+x^2-9x+6 - x^2+1 \)
Fasse gleiche Terme zusammen und vereinfache.
\[ \quad (x-2)(x^2 + 3x -3) - (x-1)(x+1) = x^3-9x+7 \]
Faktorisiere die Ausdrücke vollständig.
a)
\( \quad 3x^3+6x^2 \)
Schreibe jeden Term als Produkt von Primfaktoren
\( \quad 3x^3 = 3 \cdot x \cdot x \cdot x \)
\( \quad 6x^2 = 2 \cdot 3 \cdot x \cdot x \)
Identifiziere alle gemeinsamen Faktoren
\( \quad 3x^3 = \color{red}3 \cdot \color{red}x \cdot \color{red}x \cdot x \)
\( \quad 6x^2 = 2 \cdot \color{red} 3 \cdot \color{red}x \cdot \color{red}x \)
Der größte gemeinsame Faktor ist
\( \quad 3 \cdot x \cdot x \)
Ersetze jeden Term durch seine faktorisierte Form und schreibe den gegebenen Ausdruck um als
\( \quad 3x^3+6x^2 = \color{red}3 \cdot \color{red}x \cdot \color{red}x \cdot x + 2 \cdot \color{red} 3 \cdot \color{red}x \cdot \color{red}x \)
Klammere den gemeinsamen Faktor \( \color{red} 3 \cdot \color{red}x \cdot \color{red}x \) aus und schreibe das Obige um als
\( \quad 3x^3+6x^2 = \color{red} 3 \cdot \color{red}x \cdot \color{red}x (x+2) \)
Da \( 3 \cdot x \cdot x = 3 x^2 \) ist, wird der gegebene Ausdruck in faktorisierter Form geschrieben als
\[ \quad 3x^3+6x^2 = 3 x^2 (x+2) \]
b)
\( \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) \)
Klammere \( (x-3) \) aus
\( \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) = (x-3)(x^2 + 3x + 2- (x+1)) \)
Vereinfache \( (x^2 + 3x + 2- (x+1)) \) und schreibe das Obige um als
\( \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) = (x-3)(x^2+2x+1) \)
Beachte, dass \( x^2+2x+1 = (x+1)^2 \), daher \[ \quad (x-3)(x^2 + 3x + 2) - (x-3)(x+1) = (x-3)(x+1)^2 \]
c)
\( \quad 81 x^2 - 16 y^2\)
Da \( 81 = 9^2 \), \( x^2 = x^2 \), \( 16 = 4^2 \) und \( y^2 = y^2 \) ist, schreibe den gegebenen Ausdruck als Differenz zweier Quadrate um
\( \quad 81 x^2 - 16 y^2 = (9x)^2 - (4y)^2 \)
Wir verwenden nun die Identität für die Differenz zweier Quadrate, gegeben durch \( a^2 - b^2 = (a-b)(a+b) \), um den obigen Ausdruck zu faktorisieren
\[ (9x)^2 - (4y)^2 = (9x - 4y)(9x + 4y) \]
d)
\( \quad -6x^2+7x-2 \)
Klammere das Minuszeichen aus
\( \quad -6x^2+7x-2 = - (6x^2 - 7 x + 2) \qquad (I) \)
Um \( 6x^2 - 7 x + 2 \) zu faktorisieren, müssen wir schreiben als \( \quad 6x^2 - 7 x + 2 = ( ax + b) (c x + d) \)
wobei das Produkt \( b \cdot d = 2 \) ist, was bedeutet, dass entweder \( b = 1 \) und \( d = 2 \) oder \( b = - 1 \) und \( d = - 2 \) ist.
Das Produkt \( a \cdot c = 6 \) bedeutet die folgenden möglichen Werte: \( a = 1 \) und \( c = 6 \), oder \( a = 2 \) und \( c = 3 \) oder \( a = 3 \) und \( c = 2 \).
Nach dem Einsetzen der Werte von \( a, b, c ,d \) erhalten wir die faktorisierte Form
\( \quad 6x^2 - 7 x + 2 = (2x-1)(3x-2) \)
Setze in (I) oben ein \[ \quad -6x^2+7x-2 = - (2x-1)(3x-2) \]
Gegeben \( f(x) = -2 x^2 - 2 x + 4 \), finde
a) den Scheitelpunkt des Graphen von \( f \),
b) Die x- und y-Achsenabschnitte des Graphen der Funktion \( f(x) = -2 x^2 - 2 x + 4 \),
c) Die Symmetrieachse des Graphen von \( f \).
d) Verwende einen Taschenrechner, um \( f \) zu zeichnen und die Antworten zu Teilen a), b) und c) zu überprüfen.
a)
\( f \) ist eine quadratische Funktion und ihr Graph ist eine Parabel.
Wir schreiben zuerst die gegebene Funktion in der Scheitelpunktform \( \; f(x) = a (x - h)^2 + k \; \) durch quadratische Ergänzung, wobei der Scheitelpunkt die Koordinaten \( (h,k) \) hat.
Klammere \( -2 \) aus den Termen mit \( x \) und \( x^2\) in \( \; f(x)\) aus
\( \quad f(x) = - 2 (x^2 + x) + 4 \)
Vervollständige das Quadrat des Ausdrucks innerhalb der Klammer.
\( \quad \displaystyle \quad f(x) = - 2 \left( \left(x + \frac{1}{2}\right)^2 - 1/4 \right) + 4 \)
Vereinfache und schreibe das Obige um als
\( \quad \displaystyle \quad f(x) = - 2 \left(x + \frac{1}{2} \right)^2 + \frac{9}{2} \)
Vergleicht man die obige Funktion \( \; f(x) = - 2 \left(x + \frac{1}{2} \right)^2 + \frac{9}{2} \; \) mit der Standard-Scheitelpunktform \( \; f(x) = a (x - h)^2 + k \; \), können wir schreiben, dass \( h = - \frac{1}{2} \) und \( k = \frac{9}{2} \) ist.
Daher hat der Scheitelpunkt die Koordinaten \( \displaystyle \left(- \frac{1}{2} , \frac{9}{2} \right) \)
b)
Die x-Achsenabschnitte, falls vorhanden, sind durch die Lösungen der Gleichung \( f(x) = 0 \) gegeben, also die Gleichung
\( \quad \displaystyle \quad - 2 \left(x + \frac{1}{2} \right)^2 + \frac{9}{2} = 0 \)
Daraus ergibt sich
\( \quad 2 \left(x + \frac{1}{2} \right)^2 = \frac{9}{2} \)
\( \quad \left(x + \frac{1}{2} \right)^2 = \frac{9}{4} \)
Löse durch Ziehen der Quadratwurzel
\( \quad \left(x + \frac{1}{2} \right) = \pm \sqrt {\frac{9}{4}} \)
Vereinfache, um die beiden Lösungen zu erhalten
\( \quad \left(x + \frac{1}{2} \right) = \pm \frac{3}{2} \)
\( \quad x_1 = 1 \) und \( x_2 = - 2 \)
Der y-Achsenabschnitt ist gegeben durch \( y = f(0) = 4 \)
c)
Die Symmetrieachse des Graphen von \( f \) ist durch die vertikale Linie \( x = h = - \frac{1}{2} \) gegeben.
d)
Die Verwendung eines grafikfähigen Taschenrechners ergibt den untenstehenden Graphen, in dem der Scheitelpunkt, die x- und y-Achsenabschnitte und die Symmetrieachse mit den oben berechneten übereinstimmen.

Verwende Proportionalität, um, falls möglich, die Wertetabellen in a), b) und c) zu vervollständigen.

a)
Es gibt zwei Arten von Proportionalitätsregeln:
1) \( y \) ist direkt proportional zu \( x \), wenn es eine mathematische Beziehung zwischen \( y \) und \( x \) der Form gibt:
\( \quad \; y = k x \quad \) oder \( \quad \displaystyle \frac{y}{x} = k \quad \) wobei \( k \) eine Konstante ist.
2) \( y \) ist umgekehrt proportional zu \( x \), wenn es eine mathematische Beziehung zwischen \( y \) und \( x \) der Form gibt:
\( \quad \displaystyle y = \frac{k}{x} \quad \) oder \( \quad y \cdot x = k \quad \) wobei \( k \) eine Konstante ist.
Wir vervollständigen Tabelle a), indem wir das Verhältnis \( y / x \) und das Produkt \( y x \) wie unten gezeigt berechnen.
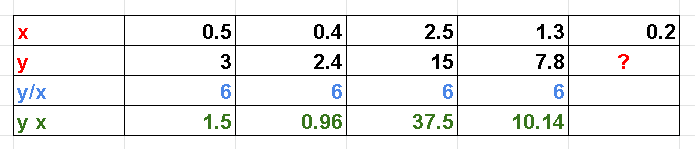
Es ist leicht zu erkennen, dass das Verhältnis konstant ist mit \( \quad \displaystyle \frac{y}{x} = 6 \quad \) und daher eine direkte Proportionalität zwischen \( y \) und \( x \) vorliegt, gegeben durch
\( \quad \displaystyle y = 6 x \quad \)
Wir vervollständigen nun die Tabelle, indem wir \( y \) für \( x = 0.2 \) berechnen, \[ \displaystyle y = 6 \cdot 0.2 = 1.2 \quad \]
b)
Wir vervollständigen Tabelle b), indem wir das Verhältnis \( y / x \) und das Produkt \( y x \) wie unten gezeigt berechnen.

Es ist leicht zu erkennen, dass das Produkt konstant ist mit \( \quad y x = 0.2 \quad \) und daher eine umgekehrte Proportionalität zwischen \( y \) und \( x \) vorliegt, gegeben durch
\( \quad \displaystyle y x = 0.2 \quad \) oder \( \quad \displaystyle y = \frac{0.2}{x} \quad \)
Wir vervollständigen nun die Tabelle, indem wir \( y \) für \( x = 20 \) berechnen, \[ \displaystyle y = \frac{0.2}{20} = 0.01 \quad \]
c)
Wir vervollständigen Tabelle c), indem wir das Verhältnis \( y / x \) und das Produkt \( y x \) wie unten gezeigt berechnen.

Es ist leicht zu erkennen, dass weder das Verhältnis \( y / x \) noch das Produkt \( y x \) konstant ist und daher in der Tabelle weder eine direkte noch eine umgekehrte Proportionalität zwischen \( y \) und \( x \) vorliegt. Daher können wir \( y \) für \( x = 11 \) in Teil c) nicht berechnen, da wir die Beziehung zwischen \( y \) und \( x \) nicht kennen.
Finde alle unbekannten Seiten und Winkel im rechtwinkligen Dreieck unten.
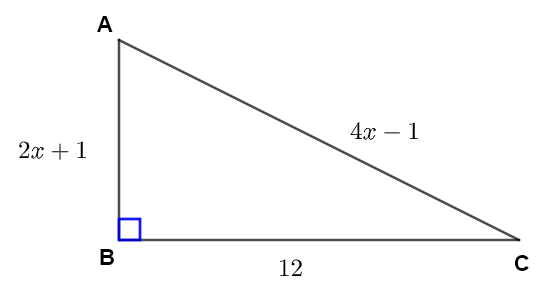
Um die unbekannten Seiten zu finden, müssen wir \( x \) finden.
Der Satz des Pythagoras , angewendet auf das gegebene Dreieck, ergibt:
\( \quad {\overline{AC}}^2 = {\overline{AB}}^2 + {\overline{BC}}^2 \)
Setze \( \overline{AC} , \overline{AB} \) und \( \overline{BC} \) mit den gegebenen Ausdrücken und Werten ein, um die Gleichung zu schreiben
\( \quad (4x-1)^2 = (2x+1)^2 + 12^2 \)
Expandiere das Quadrat, fasse gleiche Terme zusammen, vereinfache und schreibe die Gleichung in Standardform um.
\( \quad 12x^2-12x-144 = 0 \)
Dividiere alle Terme der Gleichung durch \( 12 \) und vereinfache
\( \quad x^2-x-12 = 0 \)
Löse, um zu erhalten
\( \quad x = 4 \) und \( x = -3 \)
Die Lösung \( x = - 3 \) würde \( \overline{AC} = 4 x - 1 = -13 \) ergeben, was nicht akzeptabel ist, da die Länge der Hypotenuse nicht negativ sein kann.
Nimm \( x = 4 \) und finde die unbekannte Seite und die Hypotenuse.
\( \quad \overline{AC} = 4 x - 1 = 15\)
\( \quad \overline{AB} = 2x +1 = 9\)
Unter Verwendung der Definition des Tangens des Winkels \( ACB \) haben wir
\( \quad \displaystyle \tan \angle ACB = \frac{\overline{AB}}{\overline{BC}} = \frac{9}{12} = \frac{3}{4} \)
Daher
\( \quad \angle ACB = \tan^{-1} \left(\frac{3}{4}\right) = 36.87^{\circ} \)
Die Winkel \( CAB \) und \( ACB \) sind komplementär und daher
\( \quad \angle CAB = 90 - 36.87 = 53.13^{\circ} \)
Winkel \( \alpha \) ist ein spitzer Winkel mit \( \sin \alpha = 0.6 \). Finde \( \cos \alpha\) und \( \tan \alpha\)
Betrachten wir ein rechtwinkliges Dreieck mit dem Winkel \( \alpha \), so dass
\( \quad \displaystyle \sin \alpha = \frac{Gegenkathete}{Hypotenuse} = \frac{a}{c} = \frac{0.6}{1} = 0.6 \)
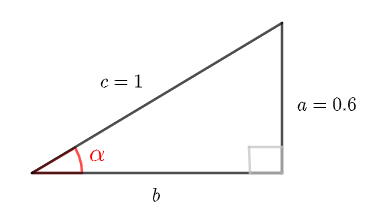
Verwende den Satz des Pythagoras, um \( b \) zu finden
\( \quad c^2 = a^2 + b^2 \)
Setze ein, um zu finden
\( \quad 1 = 0.6^2 + b^2 \)
Löse nach \( b^2 \) auf
\( \quad b^2 = 1 - 0.36 = 0.64\)
Löse nach \( b \) auf
\( \quad b = \sqrt {0.64} = 0.8\)
Wir verwenden nun die Definitionen von Kosinus und Sinus
\( \quad \displaystyle \cos \alpha = \frac{Ankathete}{Hypotenuse} = \frac {0.8}{1} = 0.8 \)
\( \quad \displaystyle \tan \alpha = \frac{Gegenkathete}{Ankathete} = \frac{0.6}{0.8} = \frac{3}{4} = 0.75 \)
In der Abbildung unten ist BE parallel zu CD. Finde die Längen \( x \) und \( y \) der Strecken CD bzw. DE.

Die Dreiecke \( ABE \) und \( ACD \) haben einen gemeinsamen Winkel \( A \).
Da \( BE \) parallel zu \( CD \) ist, sind die Winkel \( ABE \) und \( ACD \) entsprechende Winkel und daher kongruent.
Auch die Winkel \( AEB \) und \( ADC \) sind entsprechende Winkel und daher kongruent.
Die Dreiecke \( ABE \) und \( ACD \) haben alle drei Winkel kongruent und sind daher ähnlich .
Ähnliche Dreiecke haben folgende Proportionalität zwischen den Seiten
\( \quad \displaystyle \frac{\overline{AB}}{\overline{AC}} = \frac{\overline{BE}}{\overline{CD}} \)
Setze die bekannten Größen ein, um die Gleichung zu erhalten
\( \quad \displaystyle \frac{10}{10+2} = \frac{6}{X} \)
\( \quad x = 7.2 \)
Die Proportionalität der Seiten der ähnlichen Dreiecke ergibt auch
\( \quad \displaystyle \frac{\overline{AE}}{\overline{AD}} = \frac{\overline{EB}}{\overline{DC}} \)
Setze die bekannten Größen ein, um die Gleichung zu erhalten
\( \quad \displaystyle \frac{11}{11+y} = \frac{6}{7.2} \)
Löse nach \( y = 2.2 \) auf
Die Längen der Seiten AB und BC eines Dreiecks ABC betragen 14 cm bzw. 10 cm. Die Größe des Winkels C beträgt 49o. Finde alle unbekannten Winkel und alle unbekannten Seiten des Dreiecks.
Zeichne ein Dreieck und beschrifte alle bekannten Größen.

Wende den Sinussatz an
\( \quad \displaystyle \frac{c}{\sin C} = \frac{a}{\sin A} \)
Löse nach \( \sin A \) auf
\( \quad \displaystyle \sin A = \frac {a}{c} \sin C \)
Setze ein und löse nach \( A \) auf
\( \quad \displaystyle A = \sin^{-1} \left(\frac {a}{c} \sin C \right) = \sin^{-1} \left(\frac {10}{14} \sin 49^{\circ} \right) = 32.62^{\circ}\)
In jedem Dreieck ist die Summe aller drei Winkel \( A, B , C \) gleich \( 180^{\circ} \); daher
\( \quad \displaystyle \angle A + \angle B + \angle C = 180^{\circ} \)
Löse nach Winkel \( B \) auf
\( \angle B = 180 - (49 + 32.62) = 98.38^{\circ}\)
Seite \( b \) kann mit dem Sinussatz gefunden werden.
\( \quad \displaystyle \frac{b}{\sin B} = \frac{a}{\sin A} \)
Löse nach \( b \) auf
\( \quad \displaystyle b = a \frac{\sin B}{\sin A} \)
Setze ein und vereinfache
\( \quad \displaystyle b = 10 \frac{\sin 98.38^{\circ}}{\sin 32.62^{\circ}} = 18.35\)
HINWEIS Seite \( b \) kann auch mit dem Kosinussatz wie folgt berechnet werden
\( \quad \displaystyle b^2 = a^2 + c^2 - 2 a c \cos B \)
Setze ein
\( \quad \displaystyle b^2 = 10^2 + 14^2 - 2 \cdot 10 \cdot 14 \cos 98.38^{\circ} = 336.80655\)
Ziehe die Quadratwurzel, um zu finden
\( \quad b = \sqrt {336.80655} \approx 18.35 \)
Finde die Werte von \( A \) und \( B \), wenn die Gerade mit der Gleichung \( A x + By = 1 \) durch den Punkt \( (1,5) \) verläuft und einen y-Achsenabschnitt bei \( y = 3 \) hat.
Wenn die Gerade durch den Punkt \( (1,5) \) verläuft, dann erfüllen die x- und y-Koordinaten dieses Punktes die Geradengleichung. Setze daher \( x \) und \( y \) durch \( 1 \) bzw. \( 5 \) in der Geradengleichung ein, um die Gleichung zu erhalten:
\( \quad A (1) + B(5) = 1 \)
was geschrieben werden kann als
\( \quad A + 5 B = 1 \)
Die Gerade hat einen y-Achsenabschnitt bei \( y = 3 \), was bedeutet, dass die Gerade durch den Punkt \( (0 , 3) \) verläuft, daher die Gleichung
\( \quad A (0) + B(3) = 1 \)
was geschrieben werden kann als
\( \quad 3 B = 1 \)
Löse das Obige nach \( B \) auf, um zu erhalten
\( \quad \displaystyle B = \frac{1}{3} \)
Setze \( B = \frac{1}{3} \) in die Gleichung \( \quad A + 5 B = 1 \) ein
\( \quad \displaystyle A + 5 \cdot \frac{1}{3} = 1 \)
Löse nach \( A \) auf
\( \quad \displaystyle A = 1 - \frac{5}{3} = - \frac{2}{3} \)
Ein Chemiker muss 5 Liter einer 45%igen (nach Volumen) Schwefelsäurelösung herstellen. Ihm stehen 20%ige und 55%ige (nach Volumen) Schwefelsäurelösungen zur Verfügung. Er beschließt, die 20%ige und 55%ige Lösung zu mischen, um die 45%ige Lösung herzustellen. Wie viele Liter jeder Lösung müssen gemischt werden?
Sei \( x \) die Anzahl der Liter der \( 20\% \)igen Schwefelsäurelösung und \( y \) die Anzahl der Liter der \( 55\% \)igen Schwefelsäurelösung.
Wir müssen eine Lösung von 5 Litern herstellen, daher die Gleichung
\( \quad x + y = 5 \qquad (I) \)
Die Menge an Schwefelsäure in \( x \) und die Menge an Schwefelsäure in \( y \) ist gleich der Menge an Schwefelsäure in den gesamten 5 Litern; daher die Gleichung
\( \quad 20\% \cdot x + 55\% \cdot y = 45\% \cdot 5 \)
Die letzte Gleichung kann geschrieben werden als
\( \quad \displaystyle \frac{20 x}{100} + \frac{55 y}{100} = \frac{45 \cdot 5}{100} \)
Multipliziere alle Terme der obigen Gleichung mit \( 100 \) und vereinfache, um die Nenner zu eliminieren, und schreibe die Gleichung um als
\( \quad 20 x + 55 y = 225 \qquad (II) \)
Die Gleichungen (I) und (II) bilden ein Gleichungssystem, das gelöst werden muss.
Löse Gleichung (I) nach \( y \) auf, um zu erhalten
\( \quad y = 5 - x \)
Setze \( y = 5 - x \) in Gleichung (II) ein
\( \quad 20 x + 55 (5 - x ) = 225 \qquad (II) \)
Löse das Obige nach \( x \) auf
\( \quad x \approx 1.42 \) Liter
\( \quad y = 5 - 1.42 = 3.58 \) Liter
Daher müssen wir \( 1.42 \) Liter einer \( 20\% \)igen Schwefelsäurelösung und \( 3.58 \) Liter einer \( 55\% \)igen Schwefelsäurelösung mischen, um 5 Liter Schwefelsäurelösung mit einer Konzentration von \( 45\% \) zu erhalten.
Eine Familie fuhr 1000 km von Paris nach Prag in 10 Stunden. Sie fuhr einen Teil der Strecke mit einer Durchschnittsgeschwindigkeit von 80 km/h und den Rest mit einer Durchschnittsgeschwindigkeit von 120 km/h. Welche Strecke legten sie mit jeder Geschwindigkeit zurück?
Seien \( x \) und \( y \) die mit \( 80 \) km/h bzw. \( 120 \) km/h zurückgelegten Strecken.
Die Zeit für die Strecke \( x \) ist gegeben durch (Zeit = Strecke / Geschwindigkeit)
\( \quad \displaystyle t_x = \frac{x}{80} \)
Die Zeit für die Strecke \( y \) ist gegeben durch (Zeit = Strecke / Geschwindigkeit)
\( \quad \displaystyle t_y = \frac{y}{120} \)
Die Gesamtzeit für die Gesamtstrecke \( x + y = 1000 \) ist mit \( t_1 + t_ 2 = 10 \) Stunden angegeben. Daher das Gleichungssystem
\(\quad \displaystyle \left\{ \begin{aligned} x + y = 1000 \\ \frac{x}{80} + \frac{y}{120} = 10 \\ \end{aligned} \right.\)
Multipliziere die zweite Gleichung im obigen System mit dem Produkt \( 80 \cdot 120 \)
\(\quad \displaystyle \left\{ \begin{aligned} x + y = 1000 \\ \color{red}{80 \cdot 120}\frac{x}{80} + \color{red}{80 \cdot 120} \frac{y}{120} = \color{red}{80 \cdot 120} \cdot 10 \\ \end{aligned} \right.\)
Vereinfache
\(\quad \displaystyle \left\{ \begin{aligned} x + y = 1000 \\ 12 x + 8 y = 9600 \end{aligned} \right.\)
Vereinfache
Löse das System mit einer beliebigen Methode, um zu erhalten
\( y = 600 \) km und \( x = 400 \) km.
Dreieck ABC hat Eckpunkte bei den Punkten \( A(2,3) \), \( B(-3 , 4) \) und \( C \) liegt auf der vertikalen Linie \( x = -1 \). Finde alle möglichen Koordinaten von Punkt \( C \), so dass \( ABC \) ein rechtwinkliges Dreieck mit der Hypotenuse \( AC \) ist.
Sei \( b \) die unbekannte y-Koordinate von Punkt \( C (-1,b) \).
\( \quad \displaystyle \overline {AC}^2 = (2-(-1))^2+(3-b)^2 \)
\( \quad \displaystyle \overline {AB}^2 = (2-(-3))^2+(3-4)^2 = 26 \)
\( \quad \displaystyle \overline {BC}^2 = (-3-(-1))^2+(4-b)^2 \)
Dreieck \(ABC\) ist genau dann ein rechtwinkliges Dreieck mit der Hypotenuse \( AC \), wenn \( \overline {AC}^2 = \overline {AB}^2 + \overline {BC}^2 \) gilt, daher die Gleichung
\( \quad \displaystyle (2-(-1))^2+(3-b)^2 = 26 + (-3-(-1))^2+(4-b)^2 \)
\( \quad \displaystyle 2b = 28 \)
\( \quad b = 14 \)
Die Koordinaten von Punkt \( C \), so dass \( ABC \) ein rechtwinkliges Dreieck mit der Hypotenuse \( AC \) ist, sind \( (-1,14) \)
Linda gibt \( 70\% \) ihres monatlichen Budgets für Wohnen und Essen aus und gibt \( \$ 500 \) mehr für Wohnen aus als für Essen. Sie gibt \( 5\% \) ihres Budgets, das sind \( \$ 200 \), für eine monatliche Mitgliedschaft in einem Yoga-Club aus.
Wie viele Dollar gibt sie separat für Essen und wie viele Dollar für Wohnen aus?
Sei \( x \) das Budget in Dollar. Es wird gesagt, dass \( 5\% \) ihres Budgets \( \$ 200 \) sind, daher die Gleichung
\( \quad 5\% \cdot x = 200 \)
Was geschrieben werden kann als
\( \quad \displaystyle \frac{5 x}{100} = 200 \)
Löse nach \( x \) auf.
\( \quad x = 4000 \) Dollar
Seien \( h \) und \( f \) die Beträge in Dollar, die für Wohnen bzw. Essen ausgegeben werden. Es wird gesagt, dass \( 70\% \) ihres monatlichen Budgets für Wohnen und Essen ausgegeben werden, daher die Gleichung
\( \quad \displaystyle h + f = 70\% \cdot 4000 \)
Daraus ergibt sich
\( \quad \displaystyle h + f = 2800 \qquad (I) \)
Es wird gesagt, dass Linda \( \$ 500 \) mehr für Wohnen ausgibt als für Essen, daher
\( \quad h = 500 + f \qquad (II) \)
Löse die Gleichungen (I) und (II) gleichzeitig, um zu erhalten
\( \quad h =1650 , f = 1150 \)
Daher gibt Linda \( \$ 1650 \) für Wohnen und \( \$ 1150 \) für Essen aus.
Finde die Fläche des unten gezeigten Drachens, gegeben dass \( \overline {CD} = 10 \) cm.
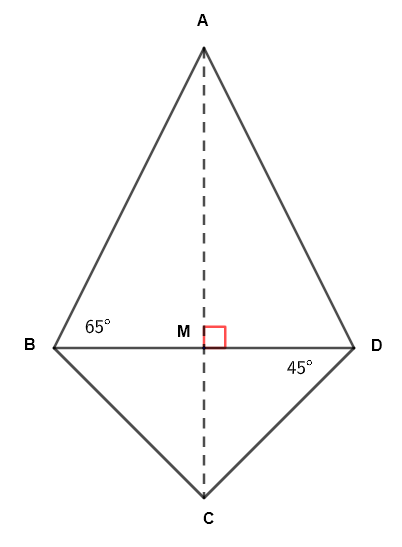
Die Fläche \( A_r \) des gegebenen Drachens ist gegeben durch
\( A_r = \frac{1}{2} \overline {AC} \cdot \overline {BD} \)
Wir müssen daher \( \overline {AC} \) und \( \overline {BD} \) finden.
Da der Winkel \( \angle MDC = 45^{\circ} \) ist, ist \( \angle MCD = 90^{\circ} - 45^{\circ} = 45^{\circ} \) und daher ist das Dreieck \( DMC \) ein rechtwinklig-gleichschenkliges Dreieck, daher
\( \quad \overline {DM} = \overline {MC} \) (gleichschenkliges Dreieck)
\( \quad \overline {DC}^2 = \overline {DM}^2 + \overline {MC}^2 \) (Satz des Pythagoras)
Das Obige ergibt
\( \quad 10^2 = 2 \overline {DM}^2 \)
Löse, um zu erhalten
\( \quad \displaystyle \overline {DM} = \frac{10}{\sqrt 2} \)
Außerdem ist der Drachen symmetrisch und daher
\( \quad \displaystyle \overline {BM} = \overline {DM} = \frac{10}{\sqrt 2} \)
was ergibt
\[ \quad \overline {BD} =\overline {BM} + \overline {DM} = \frac{10}{\sqrt 2} + \frac{10}{\sqrt 2} = 10 \sqrt 2\]
Wir bestimmen nun die Höhe \( AM \) des Dreiecks \( ABD \) unter Verwendung des Winkels \( ABM \), dessen Größe gegeben ist.
\( \quad \displaystyle \tan 65^{\circ} = \frac{\overline {AM}}{\overline {BM}} \)
daher
\( \quad \displaystyle \overline {AM} = \overline {BM} \tan 65^{\circ} = \frac{10}{\sqrt 2} \tan 65^{\circ} \)
\( \quad \displaystyle \overline {MC} = \overline {DM} = \frac{10}{\sqrt 2} \) (gleichschenkliges Dreieck)
\[ \quad \displaystyle \overline {AC} = \overline {AM} + \overline {MC} = \frac{10}{\sqrt 2} \tan 65^{\circ} + \frac{10}{\sqrt 2} \]
Wir setzen nun in die oben angegebene Formel \( A_r = \frac{1}{2} \overline {AC} \cdot \overline {BD} \) ein, um die Fläche zu erhalten.
\[ \quad \displaystyle A_r = \frac{1}{2} \left(\frac{10}{\sqrt 2} \tan 65^{\circ} + \frac {10}{ \sqrt 2} \right) \cdot 10 \sqrt 2 = 157.23 \text{ Flächeneinheiten} \].
m und n sind parallele Linien. Zeige, dass die Linien m und r senkrecht aufeinander stehen.

Beschrifte verschiedene Winkel.

Die Linien m und n sind parallel und die Linie s schneidet beide und erzeugt Stufenwinkel .
Die Winkel \( \alpha \) und \( \beta \) sind Stufenwinkel und haben daher gleiche Maße.
\( \quad \beta = \alpha = 33^{\circ} \)
Die Winkel \( \beta \) und \( \Omega \) sind Scheitelwinkel und haben daher gleiche Maße.
\( \quad \Omega = \beta = 33^{\circ} \)
Wir verwenden nun die Winkelsumme im Dreieck \( ABC \), um die Größe des Winkels \( \theta \) zu finden.
\( \quad 89 + 34 + \theta = 180 \)
Daher
\( \quad \theta = 180 - 89 - 34 = 57^{\circ}\)
Die Größe des Winkels, der von den Linien r und m gebildet wird, ist gleich \( \theta + \Omega \)
\( \quad \theta + \Omega = 57 + 33 = 90^{\circ}\)
Die Linien r und m bilden einen Winkel von \( 90^{\circ} \) und stehen daher senkrecht aufeinander.
Finde die Länge der Höhe AM der geraden quadratischen Pyramide, wenn ihr Volumen 1500 Kubikzentimeter beträgt und die Länge der Diagonalen CE ihrer Grundfläche gleich 10 Zentimetern ist.

Die Seitenlänge der quadratischen Grundfläche sei \( x \) und die Länge der Höhe AM sei \( h \). Die Formel für das Volumen \( V \) der Pyramide ist gegeben durch
\( \quad \displaystyle V = \frac{1}{3} x^2 h \)
Betrachten wir das rechtwinklige Dreieck \( CDE \), dessen Seiten die gleiche Länge \( x \) haben und dessen Hypotenuse \( CE \) die Länge 10 hat.
Verwende den Satz des Pythagoras
\( \quad x^2 + x^2 = 10^2 \)
\( \quad 2 x^2 = 100 \)
Löse nach \( x^2 \) auf
\( \displaystyle \quad x^2 = 50 \)
Wir setzen nun \( x^2 \) und das Volumen \( V \) durch ihre Werte in die oben angegebene Formel ein, um die Gleichung zu schreiben
\( \quad \displaystyle 1500 = \frac{1}{3} 50 h \)
Löse nach \( h \) auf
\( \quad h = 90 \) cm