
Fragen zur Umkehrfunktion im Zusammenhang mit geordneten Paaren, linearen, Kubikwurzel-, Quadratwurzel-, logarithmischen und exponentiellen Funktionen werden zusammen mit ihren detaillierten Lösungen vorgestellt. Die Antworten werden algebraisch und grafisch unter Verwendung der Eigenschaften einer gegebenen Funktion und ihrer Umkehrung überprüft. Um effektiver zu sein, sollten die Fragen der Reihe nach gelöst werden, da jede Frage das Verständnis der nächsten erleichtert.
Seiteninhalt
a) Finden Sie die Umkehrung der Funktion \( f \), die gegeben ist durch: \[ f = \{( -2 , 0) , (0 , 1) , (2 , 3) , (3 , 4)\} \] b) Finden Sie die Definitionsmenge und die Wertemenge der Umkehrung von \( f \).
c) Sei \( f^{-1} \) die Umkehrung von \( f \).
Berechnen Sie: \[ f(f^{-1}(1)) \; , \; f^{-1}(f(0)) \; , \; f^{-1}(f(2)) \; , \; f(f^{-1}(3)) \] d) Zeichnen Sie \( f \) und \( f^{-1} \) in dasselbe rechtwinklige Koordinatensystem und notieren Sie alle Eigenschaften von \( f \) und ihrer Umkehrung \( f^{-1} \).
Die Umkehrung von f wird gefunden, indem man die Eingabe und Ausgabe der gegebenen Funktion vertauscht. Daher ist die Umkehrung von f gegeben durch \[ f^{-1} = \{(0 , -2) , (1 , 0) , (3 , 2) , (4 , 3)\} \] b)
Definitionsmenge von \( f^{-1} \): \( \{0 , 1 , 3 , 4\} \)
Wertemenge von \( f^{-1} \): \( \{-2 , 0 , 2 , 3\} \)
c) \[ f(f^{-1}(1)) = f(0) = 1 \] \[ f^{-1}(f(0)) = f^{-1}(1) = 0 \] \[ f^{-1}(f(2)) = f^{-1}(3) = 2 \] \[ f(f^{-1}(3)) = f^{-1}(4) = 3 \] d)
Die Graphen von \( f \) (blau) und \( f^{-1} \) (rot) sind unten dargestellt.

1) Der Graph von \( f \) und der Graph von \( f^{-1} \) sind Spiegelungen voneinander an der Geraden \( y = x \).
2) Die x- und y-Achsenabschnitte auf dem Graphen von \( f \) werden zu y- bzw. x-Achsenabschnitten auf dem Graphen von \( f^{-1} \).
3) Die Definitionsmenge und die Wertemenge von \( f \) sind die Wertemenge bzw. die Definitionsmenge von \( f^{-1} \).
4) \( f(^{-1}(x)) = x \) und \( f^{-1}(f(x)) = x \)
5) Wenn die Funktion \( f \) die Umkehrung der Funktion \( g \) ist, dann ist die Funktion \( g \) die Umkehrung der Funktion \( f \) (eine Funktion und ihre Umkehrung bilden ein Paar von Funktionen).
Finden Sie die Umkehrung der linearen Funktion \( f(x) = 2x + 2 \) und zeichnen Sie \( f \) und ihre Umkehrung in dasselbe Koordinatensystem.
Schritt 1: Ersetzen Sie \( f(x) \) durch \( y \) und schreiben Sie die Funktion wie folgt als Gleichung um \[ y = 2 x + 2 \] Schritt 2: Vertauschen Sie \( x \) und \( y \) in der obigen Gleichung \[ x = 2 y + 2 \] Schritt 3: Lösen Sie die obige Gleichung nach \( y \) auf \[ 2 y = x - 2 \] \[ y = (1/2) x - 1 \] Schritt 4: Schreiben Sie die Umkehrung unter Verwendung der Notation für Umkehrfunktionen \[ f^{-1} (x) = (1/2) x - 1 \] Schritt 5: Überprüfen Sie die erhaltene Antwort mit den Eigenschaften: \( f(^{-1}(x)) = x \) und \( f^{-1}(f(x)) = x \)
Eine Möglichkeit, die erhaltene Antwort zu überprüfen, besteht darin, sicherzustellen, dass \( f(^{-1}(x)) = x \) und \( f^{-1}(f(x)) = x \) gelten.
\[ f(f^{-1}(x)) = 2(f^{-1}(x)) + 2 = x - 2 + 2 = x \]
\[ f^{-1}(f(x)) = (1/2) f(x) - 1 = (1/2)(2 x + 2) - 1 = x + 1 - 1 = x \]
Die Graphen von \( f \) und \( f^{-1} \) sind unten dargestellt, und wir können leicht sehen, dass die Graphen Spiegelungen voneinander an der Geraden \( y = x \) sind. Dies ist eine grafische Methode, um zu überprüfen, ob ein Paar von Funktionen Umkehrungen voneinander sind.
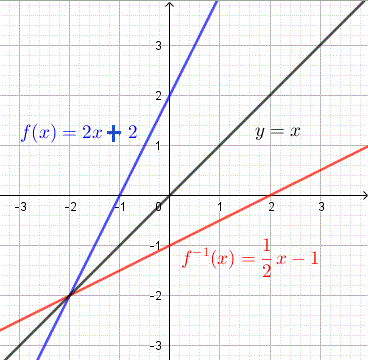
Finden Sie die Umkehrung der Funktion \( g(x) = \sqrt[3] {x - 1} \) und zeichnen Sie \( g \) und ihre Umkehrung in dasselbe Koordinatensystem.
Erheben Sie beide Seiten der Gleichung in die dritte Potenz und vereinfachen Sie
\[ x^3 = (\sqrt[3] {y - 1})^3 \]
Vereinfachen
\[ x^3 = y - 1 \]
Lösen Sie nach \( y \) auf
\[y = x^3 + 1 \]
Schritt 4: Verwenden Sie die Notation für Umkehrfunktionen, um zu schreiben
\[ g^{-1} (x) = x^3 + 1 \]
Schritt 5: Überprüfen Sie die Antwort algebraisch mit den Eigenschaften: \( g(^{-1}(x)) = x \) und \( g^{-1}(g(x)) = x \)
\[ g(g^{-1}(x)) = \sqrt[3] {g^{-1}(x) - 1} = \sqrt[3]{x^3 + 1 - 1} = \sqrt[3]{x^3} = x \]
\[ g^{-1}(g(x)) = g(x)^3 + 1 = (\sqrt[3]{x - 1)})^3 + 1 = x - 1 + 1 = x \]
Wir können leicht überprüfen, dass die Graphen der Funktionen \( g \) und \( g^{-1} \), die unten dargestellt sind, Spiegelungen voneinander an der Geraden \( y = x \) sind und daher Umkehrungen voneinander sind.

Finden Sie die Umkehrung der Funktion \( h(x) = \ln(x - 1) \) und zeichnen Sie \( h \) und ihre Umkehrung in dasselbe Koordinatensystem.

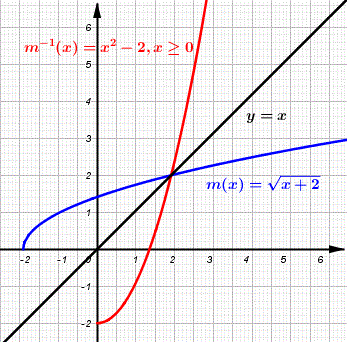
Finden Sie die Umkehrung der Funktion \( m(x) = \sqrt{x + 2} \)
Schritt 4: Verwenden Sie die Notation für Umkehrfunktionen
\[ m^{-1} (x) = x^2 - 2 \; , \; x \ge 0 ; \text {(eingeschränkte Definitionsmenge)} \]
Schritt 5: Überprüfen Sie die Antwort algebraisch
\[ m(m^{-1}(x)) = \sqrt{m^{-1}(x) + 2} = \sqrt{x^2 - 2 + 2} = \sqrt{x^2} = | x | = x \; \text{da} \; x \ge 0 \]
\[ m^{-1}(m(x)) = (m(x))^2 - 2 = (\sqrt{x + 2})^2 - 2 = x + 2 - 2 = x \]
Die unten dargestellten Graphen von \( m \) und \(m^{-1} \) sind Spiegelungen voneinander an der Geraden \( y = x \) und sind daher Umkehrungen voneinander.
Finden Sie die Umkehrung der Funktion \( t(x) = \dfrac{1}{x-1} \)
