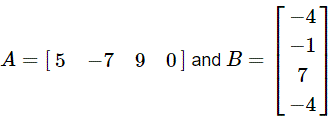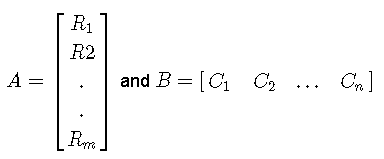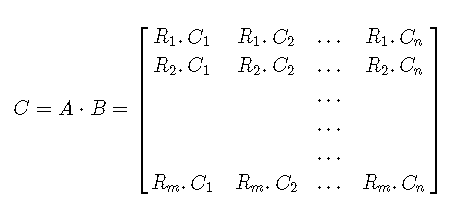Multiplication and Power of Matrices

The multiplications of matrices are presented using examples and questions with solutions.

Multiplication of Rows and Columns Matrices

Let A be a row matrix of order 1 × p with entries a 1j and B be a column matrix of order p × 1 with entries b j1 . The multiplication of matrix A by matrix B is a 1 × 1 matrix defined by:
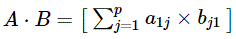
row column matrix multiplication
Example 1
Matrices A and B are defined by
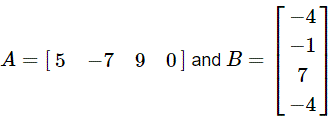
row column example
Find the matrix A B.

Solution
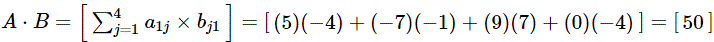
row column multiplication solution to example

Multiplication of Matrices

We now apply the idea of multiplying a row by a column to multiplying more general matrices. Let A be an m × p matrix and B be an p × n matrix. Let R 1 , R 2 , ... R m be the rows of matrix A and C 1 , C 2 , ... C n be the columns of column B and write the two matrices as:
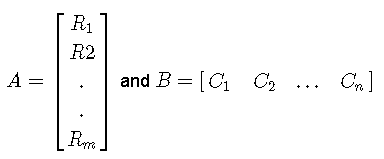
column row multiplication
The product of the two matrices A and B is matrix C of order m × n defined by
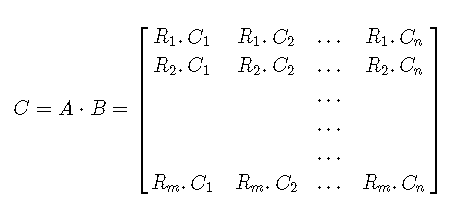
column row multiplication result

Example 2
\( \) \( \) \( \) \( \) Find the product
\( \begin{bmatrix} 2 & -1 & 0 \\ 1 & 2 & 2 \end{bmatrix} \cdot \begin{bmatrix} 2 & - 2 \\ 1 & 0 \\ -1 & 2 \end{bmatrix} \)

Solution
The matrix on the left has 2 rows R 1 and R 2 the matrix on the right has 2 columns C 1 and C 2 . Their product is given by:

\( \begin{bmatrix} 2 & -1 & 0 \\ 1 & 2 & 2 \end{bmatrix} \cdot \begin{bmatrix} 2 & - 2 \\ 1 & 0 \\ -1 & 2 \end{bmatrix} = \begin{bmatrix} R_1 \\ R_2 \end{bmatrix} \cdot \begin{bmatrix} C_1 & C_2 \\ \end{bmatrix} = \begin{bmatrix} R_1\cdot C_1 & R_1 \cdot C_2 \\ R_2\cdot C_1 & R_2 \cdot C_2 \end{bmatrix} \)

\( = \begin{bmatrix} \begin{bmatrix} 2 & -1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 1 \\ -1 \end{bmatrix} & \begin{bmatrix} 2 & -1 & 0 \end{bmatrix} \cdot \begin{bmatrix} -2 \\ 0 \\ 2 \end{bmatrix} \\\\ \begin{bmatrix} 1 & 2 & 2 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 1 \\ -1 \end{bmatrix} & \begin{bmatrix} 1 & 2 & 2 \end{bmatrix} \cdot \begin{bmatrix} -2 \\ 0 \\ 2 \end{bmatrix} \end{bmatrix} = \begin{bmatrix} (2)(2)+(-1)(1)+(0)(-1) & (2)(-2) + (-2)(0) +(0)(2) \\ (1)(2)+(2)(1)+(2)(-1) & (1)(-2) + (2)(0) +(2)(2) \end{bmatrix} = \begin{bmatrix} 3 & -4 \\ 2 & 2 \end{bmatrix} \)

Power of a Matrix

The power of a square matrix A is defined as follows:
\( A^0 = I \), \(I \) the identity matrix
\( A^n = A A .... A \) (n times) , where n is a positive integer.
If m and n are positive integers, then
\( A^m A^n = A^{m+n} \)
\( (A^m)^n = A^{m n} \)

Properties of Matrix Multiplication

  1. The product \( A B \) of two matrices \( A \) and \( B \) is defined if the number of columns of matrix \( A \) is equal to the number of rows of matrix \( B \).
  2. In general, the product of two matrices is not commutative: \( A B \ne B A \)
  3. Matrix multiplication is associative: \( (A B) C = A ( B C) \) if all the multiplications are defined.
  4. Matrix multiplication is distributive: \( A ( B + C ) = A B + A C \) and \( ( A + B ) C = A C + B C \)
  5. Multiplication by an identity matrix \( I \): \( A I = I A = A\) , this holds for square matrices of dimension n by n.
  6. For α and β real: \( \alpha ( A + B ) = \alpha A + \alpha B \)
  7. For α and β real: \( \alpha ( \beta A ) = \alpha \beta ( A ) \)
  8. For α and β real: \( (\alpha + \beta) A = \alpha A + \beta A \)
  9. For α real: \( \alpha ( A B ) = (\alpha A) B = A (\alpha B) \)

Questions on Multiplication of Matrices

  • Part 1
    A, B, C, D and E are matrices with the orders
    A: 2 × 3 , B: 3 × 5 , C: 5 × 1 , E: 1 × 5
    Which of the following are defined?
    1. \( A B \)
    2. \( A C \)
    3. \( C E \)
    4. \( E C \)
    5. \( (A B)C \)
  • Part 2
    A, B, C, D and E are matrices given by: \[ A = \begin{bmatrix} -1 & 1 & -2 \\ 0 & -2 & 1 \end{bmatrix} ,\quad B = \begin{bmatrix} -1 & 2 & 0 \\ 0 & -3 & 4 \\ -1 & -2 & 3 \end{bmatrix} ,\quad C = \begin{bmatrix} -3 & 2 & 9 & -5 & 7 \end{bmatrix} \\ D = \begin{bmatrix} -2 & 6 \\ -5 & 2 \end{bmatrix} ,\quad E = \begin{bmatrix} 3 \\ 5 \\ -11 \end{bmatrix} ,\quad F = \begin{bmatrix} -1 & 0 & 2 \\ -2 & -3 & 4 \\ 1 & 4 & -3 \end{bmatrix} \] Find if possible:
    1. \( A B \)
    2. \( B C \)
    3. \( A D \)
    4. \( E F \)
    5. \( F E \)
  • Part 3
    Find x and y if \[ \begin{bmatrix} x + y & -2 \\ x - y & 1 \end{bmatrix} \begin{bmatrix} 2 & -1 \\ 0 & -2 \end{bmatrix} = \begin{bmatrix} 8 & 0 \\ 12 & -8 \\ \end{bmatrix} \]
  • Part 4
    Calculate \[ \left( \begin{bmatrix} 2&0&0\\ 0&0&2\\ 0&2&0 \end{bmatrix} \right)^{10}\]

Solutions to the Above Questions

  • Part 1
    A, B, C, D and E are matrices with the orders
    A: 2 × 3 , B: 3 × 5 , C: 5 × 1 , E: 1 × 5
    Which of the following are defined?
    1. \( A B \) : defined because the number of columns of A is equal to the number of rows of B.
    2. \( A C \) : NOT defined, the number of columns of A is NOT equal to the number of rows of C.
    3. \( C E \) : defined because the number of columns of C is equal to the number of rows of E.
    4. \( E C \) : defined because the number of columns of E is equal to the number of rows of C.
    5. \( (A B)C \) : defined because AB is defined (see above) and the results is a matrix of order 2 by 5. The number of columns of AB is equal to 5 which is equal to the number of rows of C.
  • Part 2
    1. \( A B \) is defined and is given by
      \( A B = \begin{bmatrix} -1 & 1 & -2 \\ 0 & -2 & 1 \end{bmatrix} \begin{bmatrix} -1 & 2 & 0 \\ 0 & -3 & 4 \\ -1 & -2 & 3 \end{bmatrix} = \begin{bmatrix} 3&-1&-2\\ -1&4&-5 \end{bmatrix}\)
    2. \( B C \) is not defined because the number of columns of B is not equal to the number of rows of C.
    3. \( A D \) is not defined because the number of columns of A is not equal to the number of rows of D.
    4. \( E F \) is not defined because the number of columns of E is not equal to the number of rows of F.
    5. \( F E \) is defined and is given by
      \( F E = \begin{bmatrix} -1 & 0 & 2 \\ -2 & -3 & 4 \\ 1 & 4 & -3 \end{bmatrix} \begin{bmatrix} 3 \\ 5 \\ -11 \end{bmatrix} = \begin{bmatrix}-25\\ -65\\ 56 \end{bmatrix}\)
  • Part 3
    Find the product \( \begin{bmatrix} x + y & -2 \\ x - y & 1 \end{bmatrix} \begin{bmatrix} 2 & -1 \\ 0 & -2 \end{bmatrix} = \begin{bmatrix} 2x + 2y & -x-y+4 \\ 2x - 2y & -x+y-2 \end{bmatrix} \)
    then solve
    \( \begin{bmatrix} 2x + 2y & -x-y+4 \\ 2x - 2y & -x+y-2 \end{bmatrix} = \begin{bmatrix} 8 & 0 \\ 12 & -8 \end{bmatrix} \)

    Two matrices are equal if they have the same order and their corresponding entries are equal, hence the system of equations
    \( 2x + 2y = 8 , -x-y+4 = 0 , 2x - 2y = 12 , -x+y-2 = - 8 \)
    Solve to obtain x = 5 and y = -1
  • Part 4
    Calculate Rewrite the matrix as follows: \[ \begin{bmatrix} 2&0&0\\ 0&0&2\\ 0&2&0 \end{bmatrix} = 2 \begin{bmatrix} 1&0&0\\ 0&0&1\\ 0&1&0 \end{bmatrix} \] Hence \[ \left( \begin{bmatrix} 2&0&0\\ 0&0&2\\ 0&2&0 \end{bmatrix} \right)^{10} = 2^{10} \left(\begin{bmatrix} 1&0&0\\ 0&0&1\\ 0&1&0 \end{bmatrix} \right)^{10} \] We note that the matrix \( \begin{bmatrix} 1&0&0\\ 0&0&1\\ 0&1&0 \end{bmatrix} \) is an Row Operations and elementary matrix corresponding to interchanging rows 2 and 3. So to raise the elementary matrix to the power 10, we start with the elementary and interchange rows 2 and 3 9 times which gives the original matrix \[ \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \] Hence \[ \left(\begin{bmatrix} 1&0&0\\ 0&0&1\\ 0&1&0 \end{bmatrix} \right)^{10} = 2^{10}\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} = \begin{bmatrix} 1024&0&0\\ 0&1024&0\\ 0&0&1024 \end{bmatrix} \]

More References and links

Popular Pages

More Info