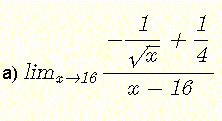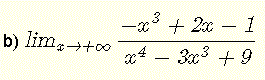Pergunta prática de cálculo 1 - A
Um conjunto de questões de Cálculo 1 com soluções detalhadas para praticar em testes, exames, exames de nivelamento,... e obter compreensão profunda sobre os seguintes tópicos:
- Funções
- Limites
- Continuidade
- Derivados
- Aplicações de Derivados
As questões foram elaboradas para cobrir os tópicos mais importantes do cálculo 1 e suas soluções detalhadas incluem links para mais prática nesses tópicos.
-
Pergunta 1
Encontre o domínio (domain) da função

-
Pergunta 2
Encontre o intervalo (range) da função

-
Pergunta 3
Encontre o inverso da função

-
Pergunta 4
Avalie cada um dos seguintes limites
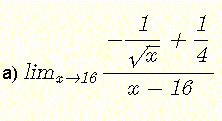
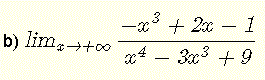



-
\( \)\( \)\( \)\( \)
Pergunta 5
a) Faça o gráfico \( y = e^{x-1} \) e \( y = x \) no mesmo sistema de coordenadas e depois mostre que os dois gráficos são tangentes no ponto \( (1,1) \) e que \( e^{x-1} \ge x \)
b) Use o resultado obtido na parte a) para determinar a concavidade da função \( f(x) = \dfrac{x^3}{6} - e^{x-1} \) e pontos de inflexão se houver.
-
Pergunta 6
Encontre a derivada das seguintes funções e não simplifique a resposta final.
a) \( f(x) = e^{x-1} + \ln (3x-1) + \sin(2x+1) \)
b) \( g(x) = (2x-1)^2(\tan(x)-1) \)
c) \( h(x) = \dfrac{x - \cos(x)}{x^2-2x+1} \)
d) \( m(x) = \sin \left(\sqrt{x^3 - \dfrac{1}{x} + 2} \right) \)
e) \( n(x) = 3^{ 2x+3} + \log_3(2x-1) \)
-
Pergunta 7
Encontre a equação da reta tangente à curva com a equação \( \sin(y^2) = x^2 \) no ponto \( ( 0,\sqrt{\pi}) \).
-
Pergunta 8
Encontre as constantes \( a \) e \( b \) para que a função \( f \) seja contínua em \( (-\infty , +\infty ) \)
\( f(x) = \left\{
\begin{array}{ll}
2x - 1 & x\le 1 \\
a x^3 + b & 1 \lt x \lt 2 \\
x + 2 b & x\ge 2 \\
\end{array}
\right. \)
-
Pergunta 9
Encontre a equação da reta tangente à curva com a equação \( y = x + \sin(x) \) em \( x = 0 \).
-
Pergunta 10
Use a definição da derivada como um limite para encontrar a derivada \( f' \) onde \( f(x) = \sqrt{x+2} \).
-
Pergunta 11
Determine em quais intervalos a função \( f(x) = e^x(x^2-5x+8)+\dfrac{x^4}{12}-\dfrac{x^3}{6 } \) côncava para cima e para baixo e qualquer ponto de inflexão.
-
Pergunta 12
Use o método de Newton com aproximação inicial \( x_1 = 2 \) para encontrar uma segunda aproximação para a solução da equação \( e^x = x^3 \).
-
Pergunta 13
Encontre o máximo e o mínimo absolutos da função \( f(x) = x^4 - x^3 \) no intervalo \( [0,5] \).
-
Pergunta 14
Se as dimensões \( L \), \( W \) e \( H\) de uma caixa retangular estão mudando às taxas \( \dfrac{dL}{dt} = 0,1 \; cm/seg \), \( \dfrac{dW}{dt} = - 0,2 \; cm/seg\) e \( \dfrac{dH}{dt} = 0,3 \; cm/seg\), a que taxa é o volume da caixa
mudando quando \( L = 20 \; cm \), \( W = 8 \; cm \) e \( H = 5 \; cm \)?
-
Pergunta 15
Quais são as dimensões do retângulo com a maior área que pode ser inscrito em um semicírculo de raio 3?
Soluções detalhadas para as questões acima
-
Solução para pergunta 1
Para que a função \( f \) assuma valores reais, a expressão sob o radical no numerador deve ser não negativa e a expressão sob o radical no denominador deve ser positiva; daí as desigualdades para resolver
\( x - 1 \ge 0 \) e \( 4 - x^2 \gt 0 \)
Os conjuntos de soluções para a primeira e segunda desigualdades são respectivamente
\( x \ge 1 \) e \( -2 \lt x \lt 2 \)
Ambas as desigualdades devem ser satisfeitas simultaneamente, portanto o domínio da função dada é a interseção dos conjuntos
\( x \ge 1 \) e \( -2 \lt x \lt 2 \) que é dado por
\( 1 \le x \lt 2 \)
-
Solução para pergunta 2
De acordo com as propriedades das funções inversas , uma maneira de encontrar o range da função dada é encontrar o domínio de sua inversa.
Vamos primeiro provar que \( f \) é uma função um para um e então encontrar sua inverso. Para provar que \( f \) é uma função injetora e, portanto, invertível, usamos a contrapositiva da função injetora e começamos com
\( f(a) = f(b) \) e prove que \( a = b \). Por isso
\( \dfrac{a - 1}{2-3 a} = \dfrac{b - 1}{2-3 b} \)
Multiplicação cruzada
\( (a - 1)(2-3 b) = (2 - 3 a)(b - 1) \)
Expandir
\( 2a - 2 - 3 ab + 3 b = 2 b - 2 - 3 ab + 3 a \)
Termos semelhantes a grupos
\(2a = 2b\)
Resolva para a
\(a = b\)
o que prova que a função \( f \) é uma função injetora e, portanto, tem uma função inversa
O inverso de \( f \) pode ser calculado começando com a equação
\( y = \dfrac{x - 1}{2-3x} \)
Multiplique cruzadamente a equação acima
\( 2 y - 3 x y = x - 1 \)
e resolva para \( x \)
\( x = \dfrac{2y + 1}{3y + 1} \)
Troque \( x \) e \( y \) na equação acima para obter o inverso \( f^{-1} \)
\(f^{-1}(x) = y = \dfrac{2 x + 1 }{3x + 1} \).
O domiano de \( f^{-1} \) é o conjunto de todos os números reais, exceto \( -\dfrac{1}{3} \). Portanto, o contradomínio de \( f \) é o conjunto de todos os números reais, exceto \( -\dfrac{1}{3} \) que pode ser escrito na forma de intervalo como
\( (-\infty , - \dfrac{1}{3}) \cup (- \dfrac{1}{3} , +\infty) \)
-
Solução para pergunta 3
Escreva a função como uma equação da seguinte maneira
\( y = \ln (2x - 3) + 2 \)
Resolva o acima para x
\( y - 2 = ln (2x - 3) \)
\(2x - 3 = e^{y - 2} \)
\(2 x = e^{y - 2} + 3 \)
\( x = \dfrac{1}{2} (e^{y - 2} + 3) \)
Intercâmbio \( x \) e \( y \)
\( y = \dfrac{1}{2} (e^{x - 2} + 3) \)
O inverso de \( f \) é dado por
\(f^{-1}(x) = \dfrac{1}{2} (e^{x - 2} + 3) \)
-
Solução para pergunta 4
a)
O limite tem a forma indeterminada \( \dfrac{0}{0} \).
Multiplique o numerador e o denominador pelo conjugado do numerador
\( -\dfrac{1}{\sqrt x} - \dfrac{1}{4} \)
\( \lim_{x\to 16} \dfrac{-\dfrac{1}{\sqrt x} + \dfrac{1}{4}}{x - 16 } \) = \( \lim_{x\to 16} \dfrac{ (-\dfrac{1}{\sqrt x} + \dfrac{1}{4})(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) }{ (x - 16)(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } \)
Simplificar
\( = \lim_{x\to 16} \dfrac{ \dfrac{1}{x} - \dfrac{1}{16} }{ (x - 16)(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } = \lim_{x\to 16} \dfrac{ \dfrac{16-x}{16x} }{ (x - 16)(-\dfrac{1}{\sqrt x} - \dfrac{1}{4}) } \)
\( = \lim_{x\to 16} \dfrac{-1}{16x(-\dfrac{1}{\sqrt x} - \dfrac{1}{4})} = \dfrac{-1}{16 \times 16(-\dfrac{1}{\sqrt 16} - \dfrac{1}{4})} = \dfrac{1}{128}\)
b)
O limite é da forma indeterminada \( \dfrac{\infty}{\infty} \).
Divida todos os termos do numerador e todos os termos do denominador por pelo termo de maior potência que em \( x^4 \)
\( \lim_{x\to +\infty} \dfrac{-x^3+2x-1}{x^4 - 3 x^3 + 9 } = \lim_{x\to +\infty} \dfrac{\dfrac{-x^3}{x^4}+\dfrac{2x}{x^4}-\dfrac{1}{x^4}}{\dfrac{x^4}{x^4} - \dfrac{3 x^3}{x^4} + \dfrac{9}{x^4} }\).
Simplifique os termos racionais
\( = \lim_{x\to +\infty} \dfrac{\dfrac{-1}{x}+\dfrac{2}{x^3}-\dfrac{1}{x^4}}{1 - \dfrac{3}{x} + \dfrac{9}{x^4} } = \dfrac{0+0-0}{1 - 0 + 0 } = \dfrac{0}{1} = 0\)
c)
O limite é da forma indeterminada \( \infty \cdot 0 \).
Seja \( t = \dfrac{3}{x} \) e reescreva o limite em termos de t.
\( \lim_{x\to +\infty} x \sin(\dfrac{3}{x}) = \lim_{t\to 0} 3 \dfrac {\sin(t)}{t} \).
Usando o resultado bem conhecido \( \lim_{t\to 0} \dfrac {\sin(t)}{t} = 1 \), o limite é avaliado como
\( = 3 \times 1 = 3\)
d)
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \dfrac{0}{0}\), forma indeterminada
Use a Regra de L'Hospital para a forma indeterminada, podemos escrever
\( \lim_{x\to 0} \dfrac{\sin(x)+x}{2x^2+x} = \lim_{x\to 0} \dfrac{ d (\sin(x)+x) / dx }{ d(2x^2+x)/dx} = \lim_{x\to 0} \dfrac{ cos(x)+ 1 }{ 4x+1} = \dfrac{ cos(0)+ 1 }{ 4\times 0+1} = 2\)
e)
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} \).
É bem sabido que o intervalo de \( \sin(x) \) é dado por
\( -1 \le \sin(x) \le 1 \)
Adicione 1 a todos os termos da desigualdade para obter a seguinte desigualdade
\( -1 + 1 \le \sin(x) + 1 \le 1 + 1 \)
\( 0 \le \sin(x) + 1 \le 2 \)
Divida todos os termos da desigualdade acima por positivo \( x \)
\( \dfrac{0}{x} \le \dfrac{\sin(x) + 1}{x} \le \dfrac{2}{x} \)
Nós temos \( \lim_{x\to +\infty} \dfrac{0}{x} = 0 \) and \( \lim_{x\to +\infty} \dfrac{2}{x} = 0 \)
Usando o teorema da compressão (ou sanduíche) , podemos avaliar o limite fornecido da seguinte forma
\( \lim_{x\to +\infty} \dfrac{\sin(x)+1}{x} = 0 \)
-
Solução para pergunta 5
a)
O gráfico de \( y = e^{x-1} \) e \( y = x \) são mostrados abaixo. A derivada de \( y = e^{x-1} \) é igual a \( y ' = e^{x-1} \) e a inclinação \( m \) da tangente em \( x = 1 \) é o valor da derivada em \( x = 1\). Por isso

\( m = y'(1) = e^{1-1}= 1 \)
A equação da reta tangente no ponto \( (1,1) \) é dada por
\( y - 1 = 1 \times (x - 1) \)
O que simplifica para
\( y = x \)
Portanto, os gráficos de \( y = e^{x-1} \) e \( y = x \) são tangentes no ponto \( (1,1) \) e podemos, portanto, afirmar graficamente que \( e^ {x-1} \ge x \).
b)
A primeira e segunda derivadas de \( f \) são dadas por
\( f'(x) = \dfrac{x^2}{2}-e^{x-1} \)
\( f''(x) = x-e^{x-1} \)
Um ponto de inflexão ocorre em um valor de \( x \) onde \( f''(x ) \) mudar de sinal. Vimos na parte a) que \( e^{x-1} \ge x \) que pode ser escrito como
\( x-e^{x-1} \le 0 \)
e portanto \( f''(x) \) é negativo e tem zero em \( x = 1 \). Portanto, o gráfico de \( f(x) \) é côncavo para baixo e não tem ponto de inflexão porque \( f''(x) \) não muda de sinal.
-
Solução para pergunta 6
a) A soma da regra de derivadas fornece:
\( f'(x) = e^{x-1} + \dfrac{3}{3x-1} + 2 \cos(2x+1) \)
b) Regra do produto de derivativos: \( g'(x) = 4(2x-1)(\tan(x)-1) + (2x-1)^2(\sec^2(x)) \)
c) regra do quociente de derivadas: \( h'(x) = \dfrac{ (1 + \sin(x))(x^2-2x+1) - (x - \cos(x))(2x-2) }{(x^2-2x+1)^2} \)
d) Deixei \( u = \sqrt{x^3 - \dfrac{1}{x} + 2} \) , escreva a função \(m \) como \(m = \sin u \) então use o regra da cadeia de derivadas
\( m'(x) = \dfrac{d m}{d u} \dfrac{d u}{d x} = \cos(u) \dfrac{1}{2}(3x^2+\dfrac{1}{x^2})(x^3 - \dfrac{1}{x} + 2)^{-1/2} \)
\( = \dfrac{1}{2} \cos \left(\sqrt{x^3 - \dfrac{1}{x} + 2} \right) (3x^2+\dfrac{1}{x^2})(x^3 - \dfrac{1}{x} + 2)^{-1/2} \)
e)
Reescreva \( 3^{ 2x+3} \) e \( \log_3(2x-1) \) como
\( 3^{2x+3} = e^{(2x+3) \ln 3}\) , mudança de base de exponenciais
\( \log_3(2x-1) = \dfrac{ \ln(2x-1)}{ \ln 3}\) , mudança de base dos logaritmos
Substitua e reescreva \( n(x) \) como
\( n(x) = 3^{ 2x+3} + \log_3(2x-1) = e^{(2x+3) \ln 3} + \dfrac{ \ln(2x-1)}{ \ln 3} \)
Agora calculamos a derivada
\( n'(x) = ( 2 \ln 3 ) e^{(2x+3) \ln 3} + \dfrac{1}{ \ln 3} \dfrac{2}{2x-1} = ( 2 \ln 3 ) 3^{2x+3} + \dfrac{2}{\ln 3(2x-1)} \)
-
Solução para pergunta 7
Primeiro diferenciamos a equação fornecida implicitamente
\( 2 y \dfrac{d y}{d x} cos(y^2) = 2 x \)
\( \dfrac{d y}{d x} = \dfrac{ x}{ y cos(y^2)} \)
A inclinação \( m \) da reta tangente é dada pelo valor de \( \dfrac{d y}{d x} \) no ponto \( ( 0,\sqrt{\pi}) \).
\( m = \dfrac{(0)}{\sqrt{\pi} cos((\sqrt{{\pi}})^2)} = 0 \)
A equação, na forma ponto-inclinação, da reta tangente à curva no ponto \( ( 0,\sqrt{\pi}) \) é dada por
\( y - \sqrt{\pi} = 0(x - 0) \)
É uma linha horizontal dada por
\( y = \sqrt{\pi} \)
-
Solução para pergunta 8
\( f(x) \) é contínuo nos intervalos \( (-\infty , 1) \) , \( (1,2) \) e \( (2 , +\infty) \). Precisamos encontrar \( a \) e \( b \) para que também seja contínuo em \( x = 1 \) e \( x = 2 \) e, portanto, contínuo em \( (-\infty , +\infty ) \).
\( f(1) = 1 \)
\( \lim_{x\to 1^-} f(x) = 1 \)
\( \lim_{x\to 1^+} f(x) = a(1)^3+b = a + b \)
Os limites à esquerda e à direita de \( 1 \) devem ser iguais
\( a + b = 1 \) (equação 1)
\( f(2) = 2 + 2 b \)
\( \lim_{x\to 2^-} f(x) = a(2)^3 + b = 8 a + b \)
\( \lim_{x\to 2^+} f(x) = 2 + 2 b \)
Os limites à esquerda e à direita de \( 2 \) devem ser iguais
\( 8 a + b = 2 + 2 b \) (equação 2)
Resolva as equações (1) e (2) simultaneamente para encontrar
\( a = \dfrac{1}{3} \) and \( b = \dfrac{2}{3} \)
-
Solução para pergunta 9
Encontre a derivada de \( y \).
\( y' = 1 + \cos(x) \)
A inclinação \( m \) da tangente em \( x = 0 \) é igual ao valor de \( y' \) em \( x = 0 \). Por isso
\( m = 1 + \cos(0) = 2 \)
A coordenada y do ponto de tangência \( P \) é dada pelo valor de \( y \) em \( x = 0 \). Por isso
\( P(0 , 0 + \sin(0)) = P(0,0) \)
A equação da reta tangente na forma ponto-inclinação é dada por
\( y - 0 = 2(x - 0) \)
e na forma de interceptação de inclinação
\( y = 2 x \)
-
Solução para pergunta 10
Definição da derivada \( f' \) da função \( f \) é dada pelo limite
\( f'(x) = \lim_{h\to 0} \dfrac{f(x+h)- f(x)}{h} \)
Substitua \( f(x) \) por \( \sqrt{x+2} \) e \( f(x+h) \) por \( \sqrt{x+h+2} \) na definição acima obter
\( f'(x) = \lim_{h\to 0} \dfrac{\sqrt{x + h +2}- \sqrt{x+2} }{h} \)
O limite acima tem a forma indeterminada \( \dfrac{0}{0} \). Multiplique o numerador e o denominador pelo conjugado do numerador
\( f'(x) = \lim_{h\to 0} \dfrac{ (\sqrt{x + h +2}- \sqrt{x+2} ) (\sqrt{x + h +2} + \sqrt{x+2} ) }{h(\sqrt{x + h +2} + \sqrt{x+2} )} \)
Expanda o numerador e simplifique
\( f'(x) = \lim_{h\to 0} \dfrac{ (x + h + 2)- (x + 2) ) }{h(\sqrt{x + h +2} + \sqrt{x+2} )} = \lim_{h\to 0} \dfrac{ h }{h(\sqrt{x + h +2} + \sqrt{x+2} )}\)
Divida o numerador e o denominador por \( h \) (ou cancele \( h \))
\( f'(x) = \lim_{h\to 0} \dfrac{ 1 }{\sqrt{x + h +2} + \sqrt{x+2} }\)
Avalie o limite e, portanto, a derivada
\( f'(x) = \dfrac{ 1 }{ \sqrt{x + 0 + 2} + \sqrt{x + 2} } = \dfrac{ 1 }{2 \sqrt{x + 2} }\)
-
Solução para pergunta 11
Encontre a primeira e a segunda derivadas
\( f'(x) = e^x (x^2-5x+8) + e^x (2 x -5) +\dfrac{x^3}{3}-\dfrac{x^2}{2} = e^x (x^2-3x+3)+\dfrac{x^3}{3}-\dfrac{x^2}{2} \)
\( f''(x) = e^x(x^2-3x+3)+e^x(2x-3) + x^2-x = e^x(x^2-x)+x^2-x = x (x - 1) e^x \)
\( f'' \) tem dois zeros: \( x = 0 \) e \( x = 1\) e \( e^x \) é sempre positivo. Portanto a tabela de sinais de \( f'' \) tem três intervalos
\( (-\infty , 0 ) \) , valor de teste \( x = -1 \) , \( f''(-1) = 2/e \) , portanto \( f''(x) \) é positivo no intervalo \( (-\infty , 0 ) \).
2)
\( (0 , 1 ) \) , valor de teste \( x = 1/2 \) , \( f''(1/2) = -\dfrac{\sqrt 2}{4} \) , portanto \( f''(x) \) é negativo no intervalo \( (0 , 1 ) \).
3) \( (1 , +\infty ) \) , valor de teste \( x = 2 \) , \( f''(2) = 2e^2 \) , \( f''(x) \) é positivo em o intervalo \( (1 , +\infty ) \).
\( f'' \) é côncavo para cima nos intervalos \( (-\infty , 0 ) \) e \( (1 , +\infty ) \) , e côncava para baixo no intervalo \( (0 , 1 ) \).
\( f'' \) muda de sinal em \( x = 0 \) e \( x = 1 \) e, portanto, tem pontos de inflexão em \( x = 0 \) e \( x = 1 \).
-
Solução para pergunta 12
Newton's method is based on the following algorithm: knowing an approximation \( x_n \) to the solution of an equation \( f(x) = 0 \), the next approximation \( x_{n+1}\) to the equation is given by
O método de Newton é baseado no seguinte algoritmo: conhecer uma aproximação \( x_n \) para a solução de um equação \( f(x) = 0 \), a próxima aproximação \( x_{n+1}\) da equação é dada por
\( x_{n+1} = x_n - \dfrac{f(x_n)}{f'(x_n)} \).
A solução para a equação dada \( e^x = x^3 \) é igual à solução da equação \( f(x) = e^x - x^3 = 0 \)
\( f'(x) = e^x - 3x^2 \)
Conhecemos uma primeira aproximação \( x_1 = 2 \); usando o algoritmo de Newton aproximamos \( x_2\) por
\( x_{2} = x_1 - \dfrac{f(x_1)}{f'(x_1)} = 2 - \dfrac{e^2 - 2^3}{e^2 - 3 \times 2^2} \approx 1.87 \) (arredondado para duas casas decimais)
Uma aproximação \(x_3\) pode ser obtida usando \( x_2 \) encontrado acima e assim por diante.
-
Solução para pergunta 13
Encontre a primeira derivada e fatore-a.
\( f'(x) = 4 x^3 - 3 x^2 = x^2(4x - 3)\)
\( f'(x) \) tem dois zeros em \( x = 0 \) e \( x = 3/4 \) e ambos estão dentro do intervalo \( [0,5] \). Os zeros de \( f'(x) \) são chamados de pontos críticos.
Agora avaliamos a função nos extremos do intervalo dado e nos zeros de \( f'(x) \).
\( f(0) = 0 \)
\( f(5) = 5^4 - 5^3 = 500 \)
\( f(3/4) = (3/4)^4 - (3/4)^3 = -\dfrac{27}{256} \)
Comparando esses valores, \( f(x) \) tem um máximo absoluto igual a \(500 \) no ponto final \( x = 5 \) e um mínimo absoluto igual a \( -\dfrac{27}{256} \) no ponto crítico \( x = 3/4 \)
Mais perguntas sobre mínimo e máximo absolutos de uma função incluídas.
-
Solução para pergunta 14
O volume \( V \) de uma caixa retangular com dimensões \( L \),\( W \) e \( H\) é dado por
\( V = L(t) W(t) H(t) \)
onde \( L(t)\) , \( W(t) \) e \( H(t) \) são funções do tempo \( t \).
Como as dimensões da caixa mudam com o tempo, o volume da caixa também muda com o tempo na taxa de variação de \( V\) é dado pela primeira derivada \( \dfrac{dV}{dt} \).
\( \dfrac{dV}{dt} = W(t) H(t) \dfrac{d L}{dt } + L(t) H(t) \dfrac{d W}{dt } + L(t) W(t) \dfrac{d H}{dt } \)
Substitua as quantidades conhecidas pelos seus valores numéricos
\( \dfrac{dV}{dt} = 8 \times 5 \times 0.1 + 20 \times 5 \times (-0.2) + 20 \times 8 \times 0.3 = 32 \; cm^3 / sec \)
-
Solução para pergunta 15
Equação de um círculo com raio \( 3 \) e centro em \( (0 , 0) \) dado por
\( x^2 + y^2 = 3^2 \)
Resolva a equação acima para y
\(y^2 = 9 - x^2\)
\( y = \pm \sqrt{9 - x^2} \)
A equação para o semicírculo superior é
\( y = \sqrt(9-x^2) \)
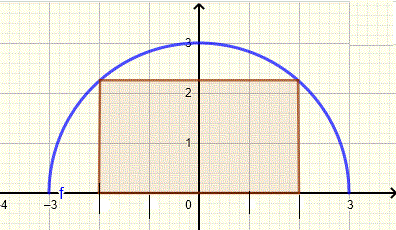
Um ponto no semicírculo com coordenada x \( x \) tem uma coordenada y igual a \(\sqrt{9 - x^2} \) (veja o gráfico abaixo)
O retângulo tem um comprimento \( L = 2x \) e uma largura (ou altura) \( W = \sqrt(9-x^2) \). A área \( A \) do retângulo é dada por
\( A(x) = L \times W = 2 x \sqrt(9-x^2) \) , \( 0 \le x \le 3 \)

Encontre a primeira derivada de \( A \)
\( \dfrac{d A}{dx} = 2\sqrt{9-x^2} + (2x) (\dfrac{1}{2}) (-2x) (9-x^2)^{-1/2} =\dfrac{2\left(-2x^2+9\right)}{\sqrt{9-x^2}} \)
Zeros de \( \dfrac{d A}{dx} \) são dados pelos zeros do numerador de \( \dfrac{d A}{dx} \)
\( -2x^2+9 = 0 \)
Dá dois zeros: \( x = \sqrt{4,5} \) e \( x = - \sqrt{4,5} \)
Consideramos o zero em \( x = \sqrt{4.5} \) pois está dentro do intervalo \( [0 , 3 ] \)
Agora avaliamos a área \( A(x) \) nos extremos \( x = 0 \) e \( x = 3 \) e no ponto crítico \( x = \sqrt{4.5} \).
\( A(0) = 0 \)
\( A(3) = 0 \)
\( A(\sqrt{4.5}) = 9 \)
A área A é máxima é para \( x = \sqrt{4.5} \)
As dimensões são:
\( L = 2 x = 2 \sqrt{4.5} \approx 4.24 \)
\( W = \sqrt(9-x^2) = \sqrt(9-\sqrt{4.5}^2) \approx 2.12 \)
Mais problemas de otimização incluídos.
Mais referências e links
Problemas de cálculo