Rational Functions

This lesson introduces rational functions and the main properties of their graphs, including the domain, x- and y-intercepts, and vertical, horizontal, and slant asymptotes. Worked examples and interactive resources are included to reinforce understanding.

Definition and Domain of Rational Functions

A rational function is defined as the quotient of two polynomial functions:

\[ f(x) = \frac{P(x)}{Q(x)} \]

The graph below represents the function

\[ f(x) = \frac{x^2 - 1}{(x + 2)(x - 3)} \]

Since the denominator equals zero at \(x = -2\) and \(x = 3\), the function is undefined at these values. As a result, the graph is discontinuous there. The dashed vertical lines indicate values where the function is undefined and foreshadow the concept of vertical asymptotes.

Graph of a rational function

Because division by zero is undefined, the domain of a rational function consists of all real numbers except those that make the denominator equal to zero.

Example 1: Finding the Domain

Find the domain of each function:

  1. \( f(x) = \frac{x + 2}{x} \)
  2. \( g(x) = \frac{x - 1}{x - 2} \)
  3. \( h(x) = \frac{x}{(x - 1)(x + 5)} \)
  4. \( k(x) = \frac{x^2 - 1}{x^2 - 9} \)
  5. \( l(x) = \frac{x^2 - 1}{x^2 + 1} \)

Solution to Example 1

  1. The denominator must not be zero: \[ x \neq 0 \] Domain: \[ (-\infty, 0) \cup (0, +\infty) \]
  2. Solve \(x - 2 = 0\): \[ x = 2 \] Domain: \[ (-\infty, 2) \cup (2, +\infty) \]
  3. Solve \((x - 1)(x + 5) = 0\): \[ x = 1,\; x = -5 \] Domain: \[ (-\infty, -5) \cup (-5, 1) \cup (1, +\infty) \]
  4. Solve \(x^2 - 9 = 0\): \[ x = \pm 3 \] Domain: \[ (-\infty, -3) \cup (-3, 3) \cup (3, +\infty) \]
  5. Since \(x^2 + 1 \neq 0\) for all real \(x\), the domain is: \[ (-\infty, +\infty) \]

Holes in the Graphs of Rational Functions

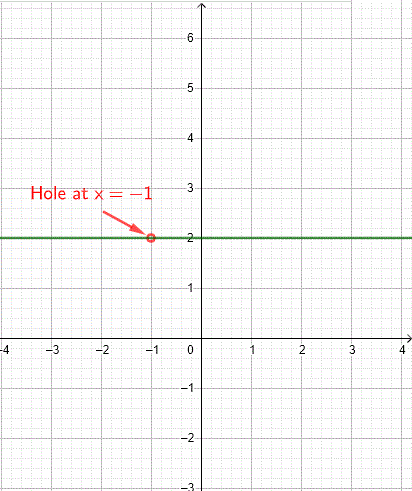
A hole occurs when the numerator and denominator share a common factor.

Example 2: Hole in a Rational Function

\[ f(x) = \frac{2x + 2}{x + 1} \]

Factor the numerator:

\[ f(x) = \frac{2(x + 1)}{x + 1} = 2, \quad x \neq -1 \]

The graph is the horizontal line \(y = 2\) with a hole at \(x = -1\).

Graph of a rational function with a hole

Vertical Asymptotes of Rational Functions

Consider the function:

\[ f(x) = \frac{1}{x} \]

The function is undefined at \(x = 0\). As \(x\) approaches zero:

\[ \lim_{x \to 0^+} f(x) = +\infty, \qquad \lim_{x \to 0^-} f(x) = -\infty \]

The vertical line \(x = 0\) is a vertical asymptote. In general, vertical asymptotes occur at zeros of the denominator that do not cancel with the numerator.

Example 3: Vertical Asymptotes

  1. \( f(x) = \frac{1}{x - 2} \)
  2. \( g(x) = \frac{x - 1}{x^2 - 1} \)
  3. \( h(x) = \frac{6}{x^2 + 2} \)

Solution to Example 3

  1. \(x - 2 = 0 \Rightarrow x = 2\) is a vertical asymptote.
  2. \[ g(x) = \frac{x - 1}{(x - 1)(x + 1)} = \frac{1}{x + 1} \] Hole at \(x = 1\), vertical asymptote at \(x = -1\).
  3. \(x^2 + 2 \neq 0\) for all real \(x\); no vertical asymptote.
Graphs of rational functions with vertical asymptotes

Horizontal Asymptotes of Rational Functions

As \(|x|\) becomes very large, the graph of \(f(x) = \frac{1}{x}\) approaches the horizontal line:

\[ y = 0 \]

Using limits:

\[ \lim_{x \to +\infty} f(x) = 0, \qquad \lim_{x \to -\infty} f(x) = 0 \]

Rules for Horizontal Asymptotes

Let \(f(x) = \frac{P(x)}{Q(x)}\), where:

Slant Asymptotes of Rational Functions

If the degree of the numerator is exactly one more than the degree of the denominator, the graph has a slant asymptote.

Example 5: Slant Asymptote

\[ h(x) = \frac{x^2}{2x - 2} \]

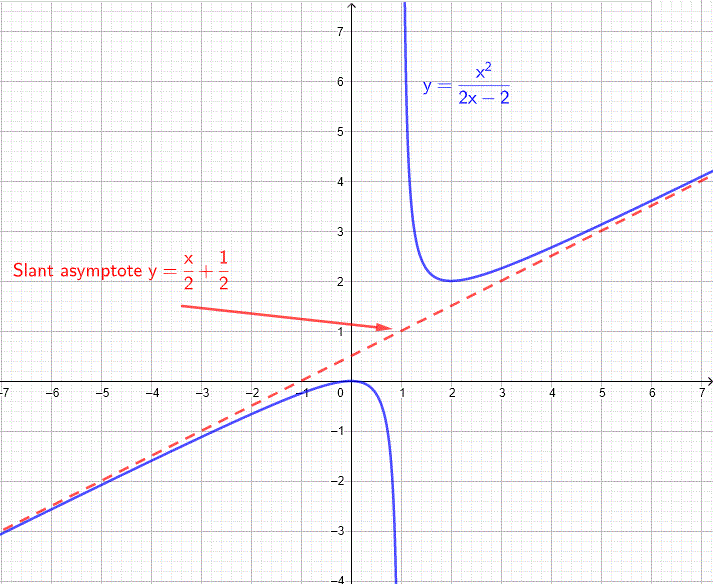
Divide:

\[ \frac{x^2}{2x - 2} = \frac{x}{2} + \frac{1}{2} + \frac{1}{2x - 2} \]

The slant asymptote is:

\[ y = \frac{x}{2} + \frac{1}{2} \] Graph with slant asymptote

More References