El módulo y el argumento de un Los números complejos se definen algebraicamente
e interpretado geométricamente. Se incluyen ejemplos con soluciones detalladas.
Se puede utilizar una calculadora de módulos y argumentos para practicar más.
Un número complejo escrito en forma estándar como \( Z = a + ib \) se puede trazar en un sistema rectangular de ejes donde el eje horizontal representa la parte real de \( Z \) y el eje vertical representa
la parte imaginaria de \( Z \). La representación geométrica de números complejos en un plano complejo, también llamado plano de Argand, es muy similar a la representación vectorial en sistemas rectangulares de ejes.
El módulo de un número complejo en forma estándar \( Z = a + ib \) se define por
\[ \color{red}{|z| = \sqrt{a^2 + b^2}} \]
y su argumento \( \theta \) está definido por
\[ \color{red} {\tan (\theta) = \left (\dfrac{b}{a} \right)} \]
Nota
Dado que la ecuación trigonométrica anterior tiene un número infinito de soluciones (ya que la función \( \tan \) es periódica), se adoptan dos convenciones principales para el rango de \( \theta \) y las llamaremos convenciones 1 y 2 para sencillez.
Convención (1) define el argumento \( \theta \) en el rango: \( 0 \le \theta \lt 2\pi \)
Convención (2) define el argumento \( \theta \) en el rango: \( (-\pi, +\pi ] \)
Los cuatro cuadrantes, tal como se definen en trigonometría, están determinados por los signos de \( a \) y \( b\)
Si el lado terminal de \( Z \) está en el cuadrante (I) o (II), las dos convenciones dan el mismo valor de \( \theta \).
Si el lado terminal de \( Z \) está en el cuadrante (III) o (IV), la convención da un ángulo positivo y la convención (2) da un ángulo negativo relacionado por
A continuación, usamos la convención (1) donde \( \theta \) está en el rango: \( 0 \le \theta \lt 2\pi \) pero también mencionamos la convención (2).
Las interpretaciones gráficas del módulo \( |Z| \) y el argumento \( \theta \) se muestran a continuación para un número complejo en un complejo.
El módulo \( |Z| \) es la longitud del segmento que representa el número complejo. Puede representar una magnitud si el número complejo representa una cantidad física. El argumento \( \theta \) es un ángulo en posición estándar (comenzando desde la dirección positiva del eje de la parte real), que representa la dirección de \( Z \)
Si nos dan el módulo \( |Z| \) y el argumento \( \theta \) de un número complejo \( Z \), entonces la forma estándar de \( Z \) viene dada por
\[ \color{red}{ Z = |Z| \; (\cos \theta + i \sin \theta) } \]
Ejemplo 1
Traza el número complejo \( Z = -1 + i \) en el plano complejo y calcula su módulo y argumento.
Solución al ejemplo 1
El número complejo \(Z = -1 + i = a + i b \) por lo tanto
\( a = -1 \) y \( b = 1 \)
\( Z \) se traza como un vector en un plano complejo que se muestra a continuación, siendo \( a = -1 \) la parte real y \( b = 1 \) la parte imaginaria.
El módulo de \( Z \) , \( |Z| = \sqrt {a^2+b^2} = \sqrt {(-1)^2+(1)^2} = \sqrt 2\) es la longitud del vector que representa el número complejo \( Z \).
El argumento \( \theta \) es el ángulo en sentido antihorario con el lado inicial comenzando desde el eje de la parte real positiva.
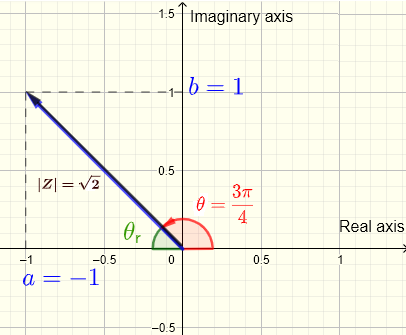
\( |Z| = \sqrt {a^2 + b^2} = \sqrt {(-1)^2 + 1^2} = \sqrt {1 + 1} = \sqrt 2\)
Primero necesitamos encontrar el ángulo de referencia \( \theta_r \) que es el ángulo agudo entre el lado terminal de \( \theta \) y el eje de la parte real.
\( \theta_r = \tan^{-1}\left|\dfrac{b}{a}\right| = \tan^{-1}\left|\dfrac{1}{-1}\right| = \tan^{-1} (1) = \dfrac{\pi}{4}\)
La parte real de \(z\) es negativa y su parte imaginaria es positiva, por lo tanto, el lado terminal de \( \theta \) está en el cuadrante II (ver gráfico de \( z \) arriba).
\( \theta \) se calcula de la siguiente manera:
\( \theta = \pi - \theta_r = \pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\)
Conclusión: Módulo: \( |Z| = \sqrt 2\) , argumento: \( \theta = \dfrac{3\pi}{4}\)
Nota Ambas convenciones (1) y (2) (ver definición arriba) dan el mismo valor para el argumento \( \theta \).
Ejemplo 2
Calcula el módulo y argumento de los números complejos:
a) \( i \) b) \( - 2 \) c) \( - i \) d) \( - 1 - 2i \) e) \( 1 - i \)
Solución al ejemplo 2
a)
Sea \( Z = i = a + i b \)
da \( a = 0 \) y \( b = 1 \)
Módulo: \( |Z| = \sqrt {0^2 + 1^2} = 1 \)
\( tan \theta = \dfrac{1}{0} = indefinido \)
Un ángulo con lado terminal en el eje imaginario tiene una tangente que no está definida.
Es más fácil determinar el argumento \( \theta = \dfrac{\pi}{2} \) a partir del gráfico de \( z = i \) que se muestra a continuación.
Nota Ambas convenciones (1) y (2) (ver definición arriba) dan el mismo valor para el argumento \( \theta \).
b)
Sea \( Z = -2 = a + i b \)
da \( a = -2 \) y \( b = 0 \)
Módulo: \( |Z| = \sqrt {(-2)^2 + 0^2} = 2 \)
\( tan \theta = \dfrac{0}{-2} = 0 \)
Un ángulo con lado terminal sobre el eje real tiene tangente igual a 0.
Podemos determinar que el argumento de \( Z \): \( \theta = \pi \) a partir de la gráfica de \( Z = -2 \) que se muestra a continuación.
Nota Ambas convenciones (1) y (2) (ver definición arriba) dan el mismo valor para el argumento \( \theta \).
c)
Sea \( Z = - i = a + i b \)
da \( a = 0 \) y \( b = - 1 \)
Módulo: \( |Z| = \sqrt {0^2 + (-1)^2} = 1 \)
\( tan \theta = \dfrac{-1}{0} = indefinido \)
Un ángulo cuya tangente no está definida es un ángulo con lado terminal en el eje imaginario.
Determinamos \( \theta = \dfrac{3\pi}{2} \) a partir de la gráfica de \( z = - i \) que se muestra a continuación.
Nota Las convenciones (2) dan \( \theta = \dfrac{3\pi}{2} - 2\pi = - \dfrac{\pi}{2}\) .
d)
Sea \( z = - 1 -2i = a + i b \)
da \( a = -1 \) y \( b = - 2 \)
Módulo: \( |Z| = \sqrt {(-1)^2 + (-2)^2} = \sqrt 5 \)
Determine el ángulo de referencia: \( tan \theta_r = |\dfrac{-2}{-1}| = 2 \) , \( \theta_r = \arctan 2 \)
El argumento de \( Z \) es: \( \theta = \pi + \theta_r = \pi + \arctan 2 \approx 4.25 \)
Nota La convención (2) da \( \theta = \pi + \arctan 2 - 2\pi = -\pi + \arctan 2 \approx -2.03444 \).
e)
Sea \( Z = 1 - i = a + i b \)
da \( a = 1 \) y \( b = - 1 \)
Módulo: \( |Z| = \sqrt {(1)^2 + (-1)^2} = \sqrt 2 \)
Determine el ángulo de referencia: \( tan \theta_r = |\dfrac{-1}{1}| = 1 \) , \( \theta_r = \dfrac{\pi}{4} \)
El argumento de \( Z \) es: \( \theta = 2\pi - \theta_r = 2\pi - \dfrac{\pi}{4} = \dfrac{7\pi}{4} \)
Ejemplo 3
Traza cada uno de los números complejos dados por su módulo y argumento y escríbelos en forma estándar.
a) \( |Z_1| = 3 \) , \( \theta_1 = 0 \)
b) \( |Z_2| = 4 \) , \( \theta_2 = 135^{\circ} \)
c) \( |Z_3| = 2 \) , \( \theta_3 = \dfrac{7\pi}{6} \)
d) \( |Z_4| = 2.5 \) , \( \theta_4 = 300^{\circ} \)
Solución al ejemplo 3
La gráfica de todos los números complejos dados se muestra a continuación.
Escribe en forma estándar.
a) \( Z_1 = 3\cos 0 + 3 \sin 0 i = 3 \)
b) \( Z_2 = 4\cos 135^{\circ} + 3 \sin 135^{\circ} i \approx -2,88 + 2,88 i \)
c) \( Z_3 = 2\cos \dfrac{7\pi}{6} + 2 \sin \dfrac{7\pi}{6} i \approx - 1.73 - i \)
c) \( Z_3 = 2\cos \dfrac{7\pi}{6} + 2 \sin \dfrac{7\pi}{6} i \approx 1,25 - 2,17 i \)
Questions
1) Calcular el módulo y argumento (en grados y radianes) de los números complejos.
\( z_1 = - 1 \)
\( z_2 = - 2 i \)
\( z_3 = -\sqrt 3 - i \)
\( z_4 = - 3 + 3\sqrt 3 i \)
\( z_5 = 7 - 7 i \)
.
2) Escribe en forma estándar los números complejos dados por su módulo y argumento. .
\( |Z_1| = 0.5 \) , \( \theta_1 = 2,1 \)
\( |Z_2| = 3.4 \) , \( \theta_2 = \pi/2 \)
\( |Z_3| = 4 \) , \( \theta_3 = 0 \)
\( |Z_4| = 12 \) , \( \theta_4 = 122^{\circ} \)
\( |Z_5| = 200 \) , \( \theta_5 = 5\pi/3 \)
\( |Z_6| = 3/7 \) , \( \theta_6 = 330^{\circ} \)
.
Soluciones a las preguntas anteriores
1)
\( |z_1| = 1 \) , \( \theta_1 = \pi \) o \( \theta_1 = 180^{\circ} \) convención(2) da los mismos valores para el argumento
\( |z_2| = 2 \) , \( \theta_2 = 3\pi/2 \) o \( \theta_2 = 270^{\circ} \) convención(2) da: \( - \pi/2 \) o \( -90^{\circ} \)
\( |z_3| = 2 \) , \( \theta_3 = 11 \pi/6 \) o \( \theta_3 = 330^{\circ} \) convención(2) da: \( - \pi/6 \) o \( -30^{\circ} \)
\(| z_4 | = 6 \) , \( \theta_4 = 2\pi/3\) o \( \theta_4 = 120^{\circ}\) La convención (2) da los mismos valores para el argumento.
\(| z_5 | = 2 \sqrt 7 \) , \( \theta_5 = 7\pi/4\) o \( \theta_5 = 315^{\circ}\) convención(2) da: \( - \pi/4 \) o \( -45^{\circ} \)
.png)
.png)
.png)
.png)
.png)
